供给侧结构性改革期间系统性金融风险的SVM预警研究

，

(成都理工大学 商学院，四川 成都 610059)

1 引言

推进供给侧结构性改革是适应和引领中国经济发展新常态的重大创新，但与此同时，推进供给侧结构性改革也将不可避免地带来债务违约率上升、银行坏账增加等一系列风险冲击，甚至还会引发系统性金融风险，从而使得中国金融安全面临更大的威胁与挑战[1,2]。正因为如此，十九大以来，中国政府反复强调，健全金融监管体系，守住不发生系统性金融风险(systemic risk)的底线。由此可见，在当前供给侧结构性改革背景下，如何构建科学有效的预警模型，维护国家金融安全与稳定，就成为金融市场主体必须高度重视和亟待解决的重要问题。

值得一提的是，自亚洲金融危机以来，金融风险预警就成了学术界关注的热点[3～6]。迄今为止，国内外学者已运用距离判别分析(distance discriminant analysis，DDA)、逻辑(Logit)回归、人工神经网络(artificial neural network，ANN)等模型对金融风险进行了预警研究，取得了较好的研究效果[7,8]。但供给侧结构性改革的推进增加了系统性金融风险特征指标的复杂性，从而可能造成训练样本的维度升高，并极大增加处理数据的难度，如果仍然使用上述模型进行风险预警，不仅会存在条件过于苛刻、过拟合、欠拟合等问题，而且极容易会陷入局部极小和维数灾难的结果，进而造成供给侧结构性改革背景下的系统性金融风险预警出现严重偏误，最终导致风险预警的失败。然而，随着计算机科学技术的突飞猛进，人工智能领域中支持向量机(support vector machine，SVM)的出现[9]，为解决上述模型在预警研究中的缺陷提供了有效途径。它能够借助核函数有效地处理高维数据，从而克服了维数灾难等问题，并具有更加优越的泛化推广性能[10～12]，因此，本文引入SVM人工智能模型对当前供给侧结构性改革期间中国系统性金融风险展开预警研究。

在对系统性金融风险的刻画问题上，尽管金融危机早前预警指标(early warning index，EWI)能够刻画一国发生金融危机的可能性，但无法对整个金融市场系统性风险进行识别[13,14]。然而，金融压力指数(financial stress index, FSI)能够对包含银行、股票、债券等众多金融市场的风险压力进行综合测度，在系统性金融风险识别上较EWI有更为突出的优势[15,16]，而且IMF[17]也提议，由联系最为密切子市场计算出的金融市场FSI可以作为衡量发展中国家系统性金融风险的主要依据。鉴于此，本文采用FSI对供给侧结构性改革期间系统性金融风险进行识别，从而为预警模型的构建奠定坚实的基础。

基于上述分析，本文先从保险、股票、债券、外汇、银行中选取最能反映该市场风险情况的指标作为系统性金融风险特征指标；然后通过累计分布函数(cumulative distribution function，CDF)加总权重法计算金融市场FSI；最后构建不同核函数下的SVM预警模型并进行模型之间性能分析，从而为金融风险管理部门防范和化解系统性金融风险，提供充分有效的决策支持与借鉴。

迄今为止，冯志峰[18]和蔡昉[19]围绕供给侧结构性改革期间中国的经济和社会问题开展了大量的定性研究，并取得了良好的效果，但令人遗憾的是，他们并没有对供给侧结构性改革中潜在的金融风险进行定量化研究。而另一些学者，如Li等[14]，Louzis 和Vouldis[15]，Luca和Peltonen[20]，许涤龙和陈双莲[16]运用了EWI、FSI等定量化方法对金融风险进行了测度研究，但他们并没有进一步对系统性金融风险开展预警研究。而也有一部分学者，如林宇等[21]基于RU-SMOTE-SVM模型对金融风险展开了预警研究，但他们并没有将预警研究纳入供给侧结构性改革的背景框架之下，甚至也没有针对系统性金融风险开展预警研究工作。

与已有的研究文献相比，本文的贡献在于，不仅将供给侧结构性改革的背景纳入到金融风险预警当中，从而为金融风险预警研究提供了新视角，而且在运用FSI测度系统性金融风险的基础上，还进一步引入人工智能领域的SVM预警模型来对供给侧结构性改革背景下的系统性金融风险进行了定量化研究，从而丰富了系统性金融风险研究内容，创新了系统性金融风险预警方法。

2 研究方法

2.1 系统性金融风险的SVM预警方法

SVM预警模型的构建需要特征指标和状态指标，因而本文使用状态指标y(t)=sgn(f(x))来表示t时期金融市场的系统性金融风险状况，其中“+1”代表存在系统性金融风险，“-1”代表不存在系统性金融风险。而每个时期都包括n维特征指标，即x(t)=(x1,x2,…,xn)。于是特征指标和状态指标就构成一组样本点(x(t),y(t))。

由于本文研究的是系统性金融风险的预警方法，即通过当前的特征指标变量预测下一时期的状态指标变量，则由t-1个不同时期的样本点就构成了一个样本数据集(x(k),y(k+1))，k=1,2,3,…，t-1,k代表了t时期前的某个时期。

在构造样本数据集的基础上，将样本数据集中一个时间长度m的样本数据(x(i),y(i+1))作为训练集,i=1,2,3,…,m,m≤k,另一部分作为测试集。然后，运用SVM对其进行训练，就可以得到如下系统性金融风险预警模型

y(i)=sgn(f(x))

(1)

其中sgn为符号函数，f(x)是以特征指标为变量的决策函数。当金融市场存在系统性金融风险时，y(i)=sgn(f(x))=+1，反之，则为-1。

使用SVM方法在训练集上寻找最优分类函数(即(1)式代表的系统性金融风险的预警模型)时，就需要把寻找最优函数转化为寻求超平面(hyper plane)之间最大分类间隔问题

为了求解(2)式的最优化问题，需要利用拉格朗日乘子(lagrange multiplier)法，将上述问题转化为对偶(dual)问题，由计算得出

(5)

其中α为拉格朗日乘子，(x(i),y(i+1))为α的一个正分量所对应的αi的样本点，K(xi,xj)为核函数。引入核函数将数据映射到高维空间(high-dimensional space)是为了解决低维(low dimension)线性不可分问题，同时又可以利用核函数内积(inner product)的性质来解决维数灾难问题。在构建的SVM预警模型过程中，由于核函数种类千差万别，不同核函数的SVM预警有着不同的性能。但在目前研究中，由于线性、多项式、Gauss径向基和二层神经网络所构建的SVM模型有着优异的预警性能。因此，本文选择这四种核函数。

(1)线性(linear)核函数

K(xj,xi)=〈xj,xi〉

(6)

(2)多项式(polynomial)核函数

K(xj,xi)=[a〈xj,xi〉+b]d

(7)

其中a,b,d为参数。

(3)Gauss径向基(radial basis)核函数

(8)

其中σ为参数。

(4)二层神经网络(sigmoid)核函数

K(xj,xi)=tanh(a〈xj,xi〉+b)

(9)

其中a,b为参数。进而，通过运用核函数到SVM中求解(4)式的对偶问题，结果如下

y(i)=sgn((w*x(i))+b*)

(10)

其中

(11)

至此，系统性金融风险预警模型的SVM方法已经构建完毕。下文将构建金融压力指数，并用计算的金融市场压力指数来识别系统性金融风险。

2.2 基于金融压力指数的系统性金融风险识别方法

金融压力指数(FSI)一方面能够较好地反映整个金融体系由于不确定性和预测损失变化所承受的总体风险压力水平，而另一方面金融压力指数与系统性金融风险又同向变化，从而通过计算金融压力指数来判断系统性金融风险变化的方向，具有定量化研究的优势，因此大多数学者运用FSI来识别系统性金融风险[15～17,22]。本文运用CDF信用加总权重法计算金融市场金融压力指数，公式如下

(12)

其中FSI即金融市场t时期的金融压力指数，mit为t时期第i个子市场的压力指数，通过对该市场的指标标准化后运用标准差倒数权重法加总而成，而wit为相对应金融子市场经济总量占整个金融市场经济总量的比例。基于上式计算出的金融市场FSI，借鉴已有国内外金融风险压力指数的研究，超过金融市场压力指数历史均值的2倍标准差时，即存在系统性金融风险[2,16]。

(13)

其中MEAN、STDV分别表示均值和标准差。当FSIP与0比较，判断是否为存在系统性金融风险的时期，从而为SVM系统性金融风险预警模型的构建提供状态指标支持。

至此，SVM预警模型和状态指标确定的方法构建完毕，下文将进一步介绍预警模型的评价方法。

2.3 系统性金融风险SVM预警模型性能的评价

为了更加全面地评价模型预警性能，本文采用综合的性能评估指标，具体方法阐述如下：

设TP和TN分别为把金融危险状态和金融安全状态预测正确的样本数量，FN和FP分别为把金融危险状态和金融安全状态预测错误的样本数量。混淆矩阵(confusion matrix)表示划分的结果。

表1 金融状态指标的混淆矩阵

通过下面3个公式得出精确率(Precision)、召回率(Recall)、F1-Score性能评价指标

(14)

(15)

(16)

其中F1-Score是Precision和Recall加权调和平均，综合了Precision和Recall的结果，当F1-Score较高时说明预警模型的性能更为优异。

受试者工作特征曲线(receiver operating characteristic curve，ROC)由在不同分类阈值(threshold)下将危险状态正确划分的概率(true positive rate，TPR)和将安全状态错误划分为危险状态的概率(false positive rate，FPR)两个变量组成

(17)

(18)

表1中TP+FP和FN+TN分别表示预测为危险状态和安全状态的样本数量，TP+FN和FP+TN分别表示实际上为危险状态和安全状态的样本数量。目前有些金融领域学者使用ROC下的面积(area under curve，AUC)来评价模型的预测性能的优劣，并且取得了良好的研究效果[21]。因而本文采用ROC曲线这一方法用于预警模型进行性能评价，更为综合地评价了预警模型性能的好坏。

3 实证分析

3.1 样本选取

本文选取保险、股票、债券、外汇、银行五大金融子市场在2002.01.01～2016.12.31的样本作为研究的对象，这既能反映金融市场整体的运行情况，也同时能反映系统性金融压力变化，具有对整个市场良好的代表性，而选择2002.01～2016.12作为研究的时间段，这是因为中国金融市场不仅经历了经济全球化带来的金融影响，而且也能反映中国金融市场从发展缓慢到高速发展期间的系统性金融风险，同时也包括了中国供给侧结构性改革期间金融压力状况的变化。

3.2 系统性金融风险预警的特征指标选取

为了准确地从五个子市场中选取出最为合适的指标作为系统性金融风险的特征指标，而又考虑到在供给侧结构性改革施行期间，金融市场受到了“三去一降一补”政策的重要影响，这就要选择既能反映子市场自身压力变化的指标，又要选择体现一些改革带来影响的指标。通过借鉴相关文献[1,2,16～18]，本文从保险、股票、债券、外汇、银行五大金融子市场当中，选取最为合适的12个指标作为系统性金融风险的特征指标，见表2。其中特征指标为2002.01～2016.12的月度数据，本文依据变量的性质把测度的指标分为正向和负向两类指标，正向指标指该指标数值越大，金融压力数值越大，负向指标反之。

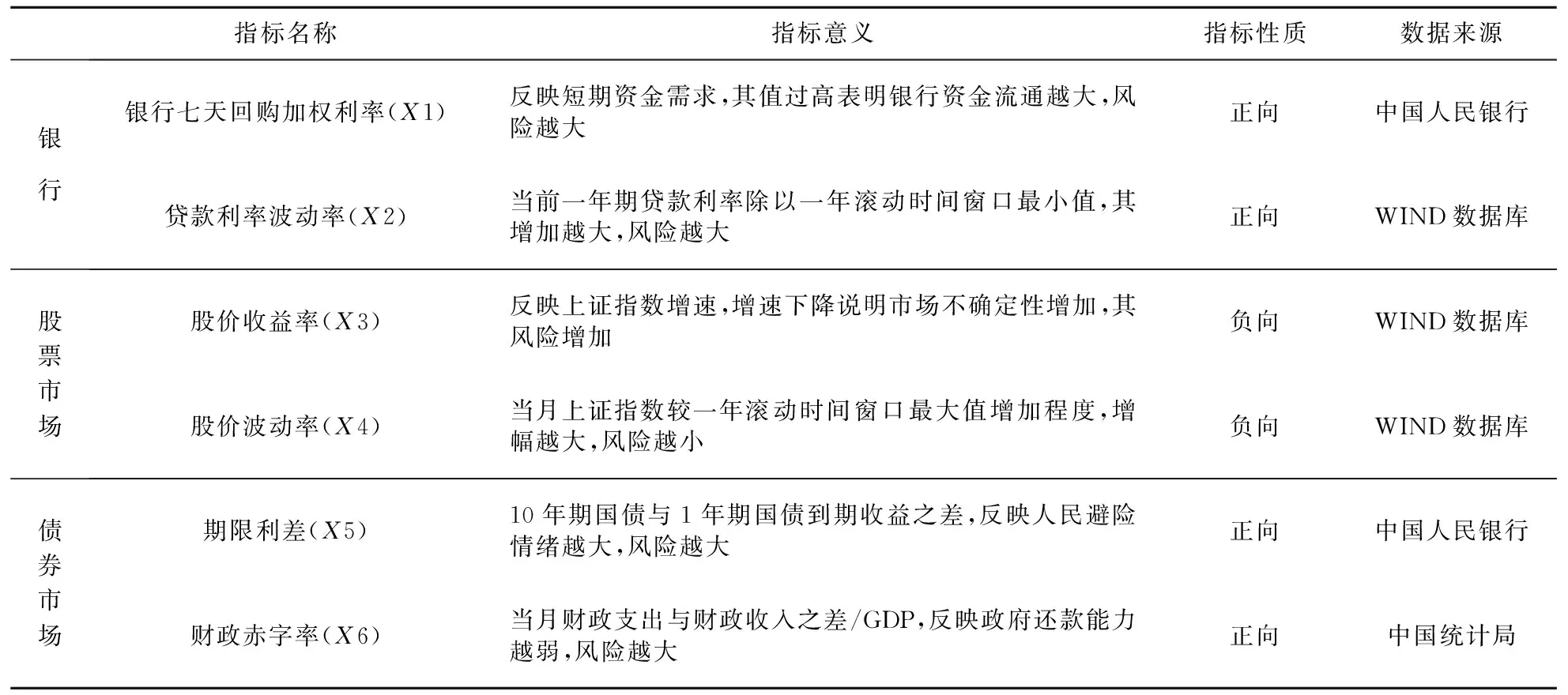
表2 五大金融子市场的12个特征指标

续表2

3.3 系统性金融风险预警的状态指标确定

状态指标是进行风险预警的关键，其划分正确与否关系到整个预警工作的成败，因而下文依据FSI方法，先对所构建的金融压力指数进行分析，再对金融市场FSI划分出的FSIP进行分析，进而论证系统性金融风险预警中状态指标划分的正确性。

下文将依据压力指数值，绘制出金融市场压力走势图，进而通过对压力指数图进行分析，验证FSI方法对系统性金融风险识别的合理性。

图1 金融市场压力走势

从金融市场来说，在图1中，金融市场FSI能准确地刻画金融体系运行情况，第一阶段2002年6月至2005年1月期间，金融市场FSI平稳而较为缓和，其大部分围绕均值波动，振幅较小。第二阶段2007年3月至2008年5月期间，金融市场FSI剧烈波动，出现了有史以来最高峰值(0.5)，反映出全球金融危机对中国金融体系造成巨大的冲击。第三阶段2011年6月至2012年5月期间，欧债危机加剧了“影子银行”、“钱荒”等问题产生的金融压力，使得这段时间金融市场FSI大幅波动。第四阶段2014年6月至2016年7月期间，银行坏账、债务违约、“股灾”等问题造成金融市场FSI逐渐走高。由此可见，所构建的金融压力指数对中国金融市场发生的大事件有较好的反映，且体现了供给侧结构性改革期间金融市场FSI变化。

在计算出的金融市场FSI的基础上，进一步获得金融市场运行的状态FSIP，见图2，其中当FSIP大于0时，为存在系统性金融风险的时期，FSIP小于等于0时，为不存在系统性金融风险的时期。

图2 系统性金融压力时期识别

一方面，从图2的走势可以观察得出和金融市场FSI指数走势基本一致，因此可以验证运用金融市场FSI划分的金融市场压力时期较为合理。另一方面，从图2可以发现虽然中国金融市场处于安全时期数量远远多于危险时期数量，总体来说中国金融市场的运行是处于较为安全的状态，但是仍要仔细对待中国的系统性金融风险，因为系统性金融风险有导致金融危机的可能，会在金融市场上引发剧烈的连锁反应，使经济和就业遭受重大冲击。下文将探索出最优的系统性金融风险预警模型。

3.4 最优核函数SVM预警模型的确定

首先本文是运用滚动预测的方法，即用一段时间的样本作为训练集预测这段时间下一个时间的值，再把这个样本加入到先前的预测样本中来进行预测下一个时间的值，一直持续到需要被预测期间样本状态指标预测完结束。下面将采用2002.01～2011.09，2002.01～2012.09，2002.01～2013.09和2002.01～2014.09期间(以下简称第一、第二、第三和第四段时间区间)的样本作为训练样本建模。本文主要是使用的Matlab2016a进行编程分析，实证结果见表3。

表3 不同核函数对四个时间区间的预测准确率

在Accuracy方面，用多项式核函数来构建系统性金融风险SVM预警模型在每个预测时间段区间的准确性都最为优秀。同时，从表3中F1-Score和AUC值可见，多项式核函数所构建的SVM预警模型评价指数值也高于其他三种核函数，因此总体上可以证明多项式核函数下的SVM预警模型的性能更为优异，可以作为最优SVM预警模型来对系统性金融风险开展研究。

3.5 最优SVM模型与其余模型的预测性能对比

虽然通过上述的反复测试，得出了最优SVM预警模型，但是，是否较其他模型更具有预测的性能优势，还不得而知。本文接下来需要进一步探讨SVM预警模型的有效性。

表4 不同预警模型的性能对比

注：产生0值的原因是DDA模型把所有的系统性金融风险样本都判断错误。

由表4可知，Accuracy, F1-Score和 AUC 值为不同预警模型在四个时间区间的预测性能的指数，但SVM预警模型每个预测时间区间的评价指数都高于其他三种预警模型，由此说明SVM预警模型较其他三种预警模型有更好的预测性能。下文将运用最优的系统性金融风险SVM预警模型以2012.10～2015.11期间的样本建立模型来对供给侧结构性改革2015.12～2016.11这一段期间的风险状况进行预测分析。

3.6 最优SVM预警模型对供给侧结构性改革期间系统性金融风险的预测

通过运用最优SVM预警模型对供给侧结构性改革2015.12到2016.11期间进行预测研究，其预测结果表明模型的预测准确率达到83.33%，具有优秀的预测能力，因此可以说明本文探索出的SVM预警模型对供给侧结构性改革期间的系统性金融风险有优越的预警性能，能够为金融风险管理部门防范和化解系统性金融风险，维护金融安全与稳定并保障供给侧结构性改革的顺利推进提供充分有效的决策支持与借鉴。

4 结论与启示

本文以金融市场为研究对象，基于四种核函数探索最优核函数SVM模型，并运用FSI方法从保险、外汇、股票、债券和银行五大主要金融子市场中选取了对FSI有重要影响样本指标，并进一步划分出系统性金融风险的状态指标作为最优SVM模型的输入变量，建立起中国系统性金融风险SVM预警模型；针对SVM预警模型的预测能力的优劣，使用Logit回归，BPNN和DDA等模型进行对比分析。实证结果表明，系统性金融风险SVM预警模型能够反映金融市场风险状态变化的情况，同时与上述模型性能对比来看，无论是从模型的预测准确性进行分析，还是从综合的预测能力评价指标F值和AUC值分析，系统性金融风险SVM预警模型在预测系统性金融风险状态上都具有优越的预测性能。

本文的研究表明，金融压力指数与SVM相结合可以较好地监测金融市场风险的变化，并且能有效地预测系统性金融风险的状态，进而帮助金融风险监管者和政策制定者及时准确地前瞻性评估潜在发生系统性金融风险的可能性，防范和化解系统性金融风险，避免爆发金融危机。但需要指出的是，预警仅仅是防范风险的第一步，风险管理部门还应该关注应对措施的制定和实施，由于金融市场之间存在着紧密的相互关系，所以在供给侧结构性改革推进中，可能会使金融子市场之间的风险传递产生连锁反应，而且为了防止金融债务过高企业所出现利息负担过重，甚至资不抵债的局面，在运用“去杠杆”政策激发企业活力的过程中，如果去金融债务的杠杆不够精准，将会不可避免地带来债务违约率上升、银行坏账增加等一系列风险冲击，甚至还会引发系统性金融风险，从而使得中国金融安全面临更大的威胁与挑战。因此，在政策推行的过程中，需要考虑到各市场的关联性以及承受力，只有深入分析金融体系的复杂性特征，才能有效地监管风险的扩散途径，把金融风险控制在可承受的范围之内，进而守住不发生系统性金融风险的底线。