基于指数函数的电池剩余放电时间预测模型

侯国亮，熊青雪月，王君婷

(长春师范大学数学学院，吉林长春 130032)

1 研究背景

铅酸电池是一种电极由铅及其氧化物制成，电解液是硫酸溶液的蓄电池.因电压稳定、价格便宜等优点，铅酸蓄电池在交通、通信、电力、军事、航海、航空等领域都有着广泛的应用.然而，在实际生活中，由于对铅酸电池使用方法不当等原因，致使原有的电池能量未被完全应用，从而造成了对环境的污染以及能量的浪费.相关研究表明，一个小小的钮扣铅酸电池可污染600立方米水，相当于一个人一生的饮水量；而被误认为成废电池丢弃后，电池的外壳会慢慢地腐蚀，其中的重金属物质会逐渐渗入水体和土壤，造成污染.重金属污染的最大特点是它在自然界不能降解，只能迁移.所以可以毫不夸张地说铅酸电池从其被发明的那一刻起就注定会对环境造成极大威胁.为了尽可能减少铅酸电池对人类赖以生存的环境的破坏并节约能源，使其更好地服务于人类，准确预测铅酸电池在当前负荷下的剩余放电时间是使用中必须解决的问题.

由于数学建模法具有成本低、无污染、易操作、可通用、时间短、重复性高和灵活性强等优点，所以通过建立数学模型预测铅酸电池在当前负荷下的剩余放电时间是一项具有重要理论和实际意义的工作.本文依据前期采样数据，运用最小二乘法拟合建立符合实际的预测电池剩余放电时间的数学模型(也称放电曲线)，并给出该数学模型的正确性检验.

2 建立模型

步骤一，运用Matlab数学软件绘制采样数据散布图，即电压与放电时间关系图，如图1所示.

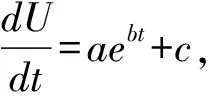
U(t)=eat+b+ct+d.

(1)

其中，a,b,c,d是四个待定常数.

步骤三，采用最小二乘法确定模型(1)中的四个待定常数.

下面就以电流I=20 A时的情形为例来解释说明如何运用最小二乘法确定模型(1)中的待定常数.

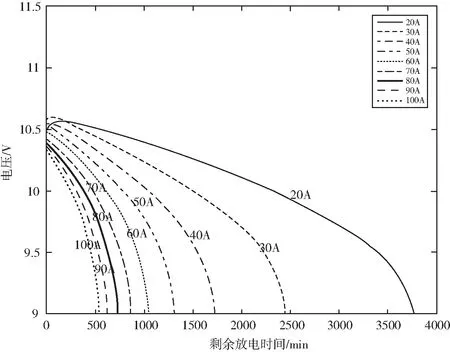
图1 电压和电池放电时间关系

首先，构造目标函数：

(2)

其中，(ti,Ui)，i=1,2,…,m表示前期采样数据对.

然后，按照最小二乘准则，问题归结为：求a,b,c,d使得Φ(a,b,c,d)最小.进而，上述问题又可转化为求解非线性方程组(3).

(3)

最后，使用数学软件Matlab编程求解非线性方程组(3).结果如下：

a=-7.1328，b=-0.8，c=0.000081376，d=10.567.

所以，当电池以恒定电流I=20A进行放电时，电压U与放电时间t之间满足的函数关系式为：

UI=20(t)=exp(-7.1328t-0.8)+0.000081376t+10.567.

同理可得，当电池分别以恒定电流30A、40A、50A、60A、70A、80A、90A和100A进行放电时，电压U与放电时间t之间满足的函数关系式依次为：

UI=30(t)=exp(-1.449t-0.7)+0.00017595t+10.583，UI=40(t)=exp(-3.2688t-0.7)+0.00018034t+10.537，UI=50(t)=exp(-5.544t-0.7)+0.0002048t+10.492，UI=60(t)=exp(-8.6298t-0.7)+0.00024295t+10.457，UI=70(t)=exp(-1.328t-0.6)+0.00022779t+10.397，UI=80(t)=exp(-1.7977t-0.6)+0.00028628t+10.364，

UI=90(t)=exp(-2.468t-0.6)+0.00032746t+10.334，UI=100(t)=exp(-3.0117t-0.6)+0.00048779t+10.311.

3 模型检验

3.1 平均相对误差检验法

运用“平均相对误差”指标对上述各模型进行正确性检验.根据有关专业知识可知，利用放电曲线预测电池剩余放电时间的精度取决于放电曲线在低电压段的质量.但是，放电曲线等时间间隔采样在低电压段的采样点相对稀疏.基于这个事实定义平均相对误差(MRE).

定义1 从额定的最低保护电压开始按不超过0.005 V的最大间隔提取k(≥231)个电压样本点.这些电压值对应的模型已放电时间与采样已放电时间的相对误差的平均值称为平均相对误差.

显然，平均相对误差值越小，对应的放电曲线模型就越精确、越稳定.

依据平均相对误差定义，借助Matlab数学软件编程计算第2节中各个模型的平均相对误差值，结果如表1所示.

表1 平均相对误差

由表1计算结果表明，各模型正确有效.

3.2 预测剩余放电时间检验法

通过对比当前负荷(9.8 V)下的剩余放电时间预测值和实测值给出第2节中各模型的正确性检验.根据各放电曲线的数学表达式，借助Matlab数学软件编程计算出各模型在当前负荷(9.8 V)下的剩余放电时间(预测值).结果如表2所示.

表2 当前负荷电压9.8V时的剩余放电时间预测值和实测值对照表

由表2所示数据表明，各模型正确有效.