透镜与球面镜成像规律探讨

罗 涛，唐雯婷

(长春师范大学物理学院，吉林长春 130032)

通常的光学教材，一般只给出了透镜与球面镜成像的基本公式，讨论在特定例题中的成像性质，并没有系统地总结其整体的成像规律，这将影响学生对光学问题的判断。本文根据球面反射、折射和薄透镜成像的基本公式，拟合出物距与像距之间的曲线关系图，据此对其成像规律进行了总结，并对处在不同位置物体的成像性质进行了分析，从而进一步加深学生对光学知识的理解与掌握。

1 球面反射、折射、薄透镜成像的基本公式

薄透镜成像的物像公式为：

(1)

其中，n2为像方介质折射率，n1为物方介质折射率，n为透镜本身材料的折射率，s′为像距，s为物距。

在式(1)中，令r1=r2=r，则有：

(2)

式(2)为球面折射的物像公式。

在式(2)中，令n1=-n2=-n，则得到：

(3)

式(3)为球面反射的成像公式。

2 成像的性质

在光学系统中，物与像的性质包括像的虚、实、正立、倒立、放大、缩小这几种情况。其中，横向放大率是用于判断透镜成像性质的关键因素之一。

将透镜成像的横向放大率定义为像的大小与物的大小的比值，公式为：

(4)

球面折射的横向放大率公式为：

(5)

球面反射的横向放大率公式为：

(6)

3 物像关系与性质分析

3.1 薄透镜成像对应的物距与像距关系

图2是凹透镜成像关系曲线图，其中，n1=1，n2=1，n=1.5，r1=-10 cm，r2=10 cm。从曲线中可以清楚地看出规律，分析过程与图1大同小异。各象限成像性质相似，其中由于实物为发散的入射光束的交点，而凹透镜具有发散作用，所成的像必定为发散光束的交点，为虚像。因此图2中第二象限实物不能成实像。

图1 凸透镜成像关系曲线图

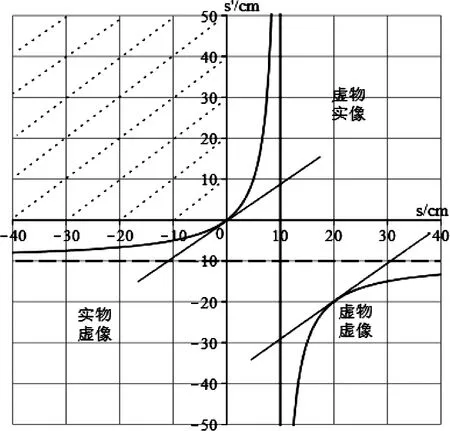
图2 凹透镜成像关系曲线图

3.2 球面折射成像对应的物距与像距关系

图3为凸球面镜折射成像的关系曲线图，其中，n1=1，n2=1.5，r=10 cm。图4为凹球面镜折射成像关系曲线图，其中，n1=1，n2=1.5，r=-10 cm。图3与图4所示同样为折射，性质相同，其成像规律与图1、图2相似。但依据公式(5)，球面折射所成像的大小还与透镜和介质的折射率有关，不能由直线y=x直观地看出，需要根据具体情况进行分析。

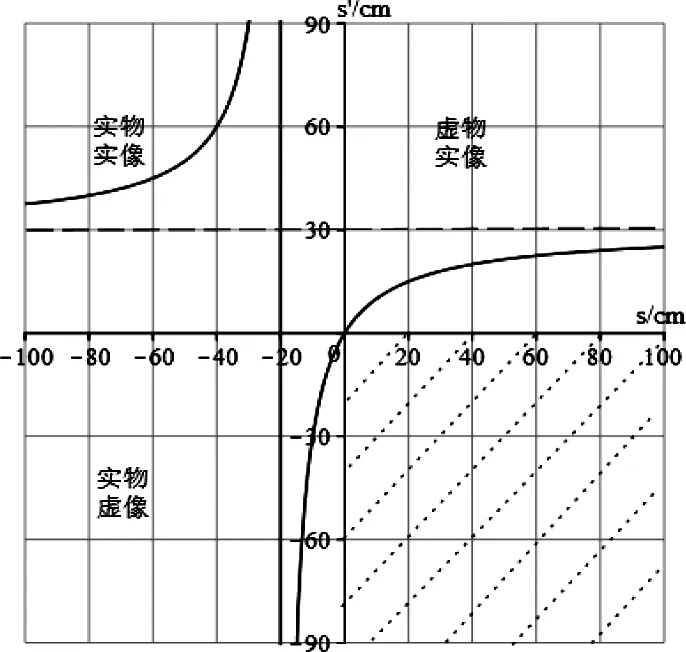
图3 凸球面镜折射成像的关系曲线图

图4 凹球面镜折射成像关系曲线图

3.3 球面反射成像对应的物距与像距关系

图5是焦距f=f′=20 cm的凸球面反射成像的关系曲线图。根据反射性质，光线的传输与球面镜折射恰好相反，若像成在物空间，即s′<0，则像点为会聚光束的交点，为实像；若像不成在物空间，即s′>0，则像点为反向延长线的交点，为虚像。根据两条辅助线判断像的放大或缩小，根据公式(6)判断像的正立或倒立。则第一象限为虚物成倒立虚像；第二象限为实物成正立缩小虚像；第四象限为虚物成正立放大实像；在第三象限中，根据凸球面反射特点，发散光束经反射后不能会聚，故实物不成实像。

图6是焦距f=f′=-20 cm的凹球面反射成像关系曲线图。与图5的分析方式相同，其中第一象限由于在凹球面反射中，会聚光束经反射后仍会聚。故虚物不成虚像。

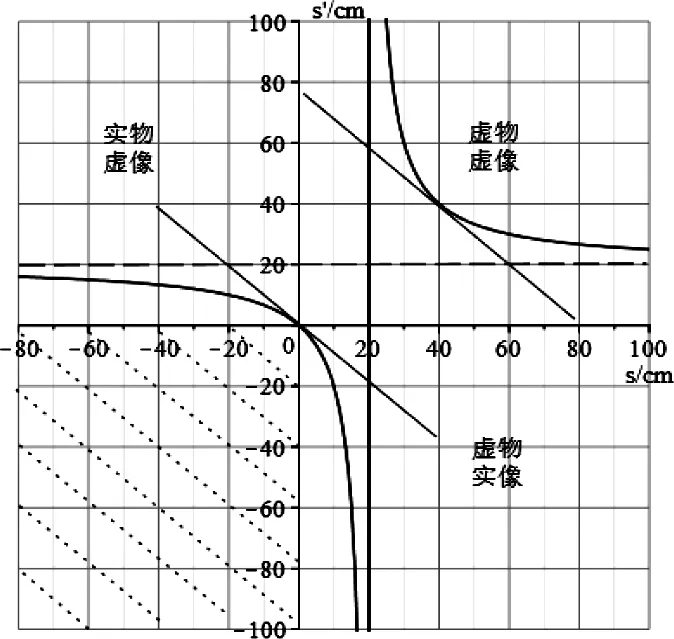
图5 凸球面反射成像关系曲线图

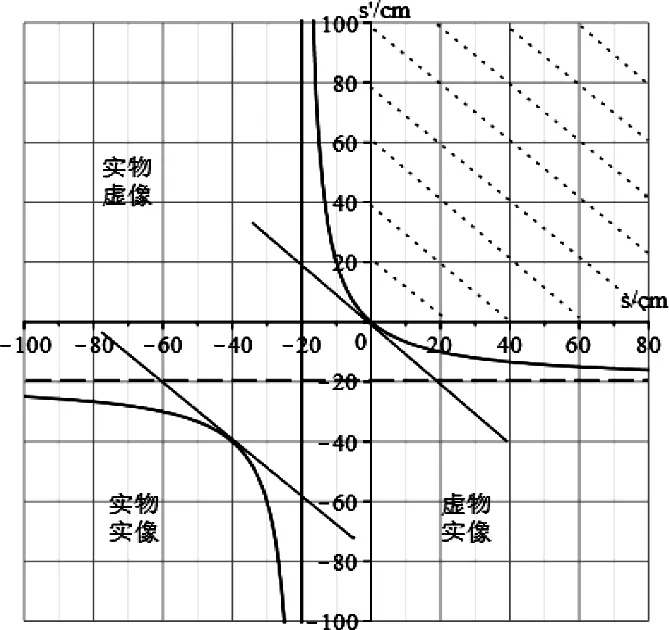
图6 凹球面反射成像曲线图

4 结语

通过以上的分析，可以清楚地从各个物距与像距的关系图中看出其成像的规律，以及其所成像的性质。例如，在透镜成像时，当s>0，s′>0时，对应着图1的第一象限，即虚物成实像。在三种光学系统中，虚物能成实像，则实物亦能成虚像；而若实物能成实像则虚物必不能成虚像，反之亦然。此方法一目了然，方便学生的理解、记忆与掌握。