采用RBF对柔性机械臂进行逆动力学分析

郎英彤，辛原野

(吉林建筑大学城建学院，吉林长春 130118)

近年来，柔性机器人以其结构轻巧、荷载/重量高、操作空间较大、能耗低等诸多优点受到广泛关注。然而柔性机械臂在运动时所产生的弹性弯曲变形和振动，会使其定位不准确，使得对柔性臂机器人的控制和分析已成为一个具有挑战性的问题。

柔性机械臂动力学建模的目的是为了描述柔性机械臂的动力学行为，特别是为了确定柔性体所产生的变形和振动，以保证柔性机械臂末端的准确定位和在运动过程中的准确轨迹。而传统的建模方式将柔性杆件运动过程中可能发生的一系列不确定因素进行近似忽略，因此在该基础上建立起来的数学模型具有一定的不准确性，直接影响对杆件的控制，从而降低末端运动轨迹的准确性。科技发展越来越迅猛的今天，无论是航天、能源、国防,还是汽车、机械等领域，对轨迹精度要求都越来越高，传统方法已然不再适用，因此本文提出RBF神经网络方法。

1 理论分析

柔性系统无法通过纯运动几何学将末端物体的位置、姿态变量与各关节变量间的关系一一对应，它们之间的关系必须通过动力学控制方程的求解才能建立起来[1]，下面对该系统进行逆动力学分析。

本文研究的单柔性机械臂简图如图1所示，杆件为均匀欧拉梁，其质量为M，长度为l，驱动力矩为τ(t)，且忽略重力的影响。

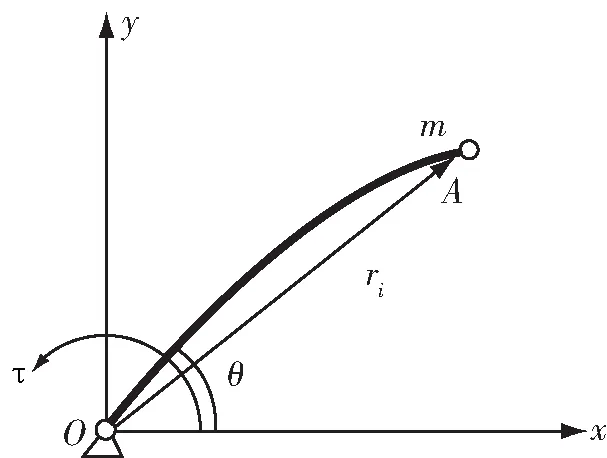
图1 单柔性机械臂简支梁模型

图2 杆件的运动简图

图2为杆件的运动简图，XOY为惯性坐标，r是惯性坐标中的位置矢量，xOy为相对坐标系(或动坐标)，r′是动坐标中的位置矢量。向量r在XOY和xOy坐标系中的投影关系为：

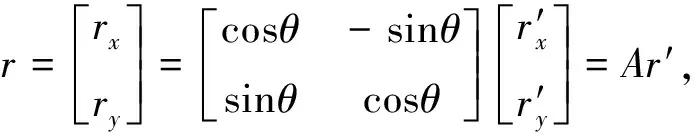
A为坐标转换矩阵；θ为OX轴与Ox轴之间的夹角，即机械臂的刚性转角。

对于杆件的变形关系,本文采用Rayleigh-Ritz方法来描述，令杆件的横向位移v(x,t)=Φ(x)qf(t)。

其中，Φ(x)取简支梁模态函数，模态取二阶Φ(x)=[Φ1(x) Φ2(x)]，qf=[qf1qf2]T。其中，qf1、qf2分别对应杆件任意截面的挠度与转角的广义坐标。

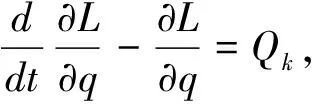
L=T-U-V.

其中，

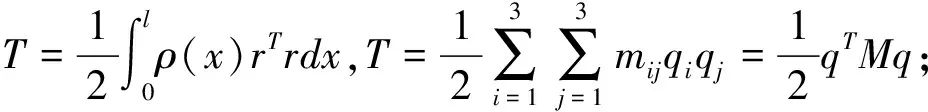
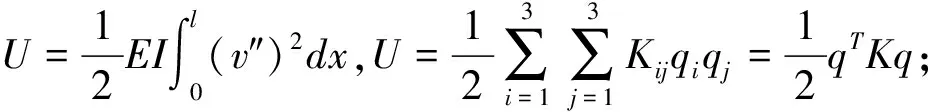
V表示重力势能，本文忽略重力势能。

其中，

q表示系统的广义坐标，q=[θqf1qf2]T=[q1q2q3]T；

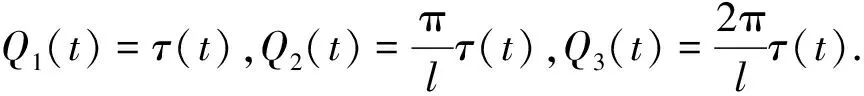
由于该系统控制方程具有强耦合性和非线性[3]，通常得不到相应的解析解，所以必须借助于数值计算方法。基本上可分成两大类[4]：一类是拉格朗日乘子法，通常称为最大未知量法；另一类是全部用独立的广义坐标描述的纯微分方程组，通常称为最小未知量法。其中拉格朗日乘子法即通过引入拉格朗日乘子释放系统的约束，在控制方程中包括独立和不独立两种广义坐标形式，并且又包含了待定乘子，这样就构成了系统的运动微分方程与约束方程相结合的动力学控制方程，即为微分-代数混合方程组。

目前一般采用传统的近似法进行求解，该方法的思想是：先忽略弹性变形对整体刚性运动的影响，得到初步驱动力矩后，将其带入柔性机械臂方程中求解弹性变量，再将给定的刚性变量和弹性变量一起作为初值，重新带回动力学方程中。由于该方法不会造成端点轨迹的定性差别，所以该方法仍在广泛应用。

对于近似方法产生的误差造成末端轨迹不精准、不能满足使用要求等问题，可以借助于RBF神经网络方法来解决，该方法具有拟合非线性方程、较好的耐故障能力和较快的总体处理能力，以及自适应性、适应集成、多变量系统的特点，可以解决柔性杆件运动中产生的不确定因素[5]。根据这些特点，本文采用该方法对系统动力学进行数值仿真，并与近似方法进行比较。

2 数值仿真

(1)采用近似方法[6]对系统动力学方程进行数值仿真[7]。机械臂的物理和几何参数如表1所示。

初始条件：θ=2t3-3t2，当t=0时运动变量θ=0，θ′=0，弹性变形qf1=qf2=0。挠度qf1、qf2与时间t的关系曲线见图3和图4，刚性转角θ实际轨迹与理想轨迹随时间t变化的曲线见图5。

表1 机械臂的物理和几何参数

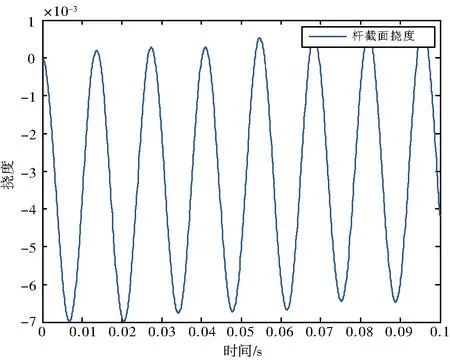
图3 挠度qf1与时间的关系曲线

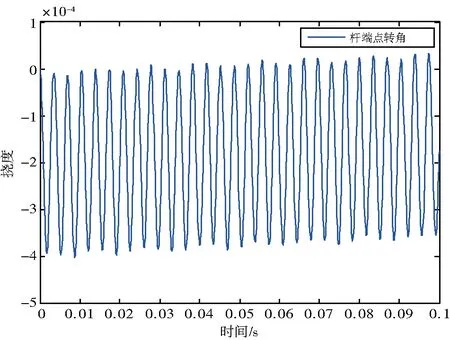
图4 挠度qf2与时间的关系曲线

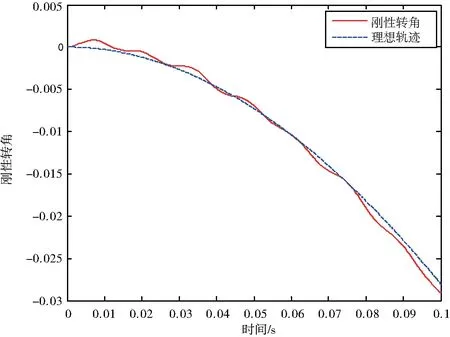
图5 刚性转角θ实际轨迹与理想轨迹随时间变化的曲线

(2)采用RBF神经网络法进行数值仿真。1985年Powell提出，径向基函数网络(Radial Basis Funtion，RBF)是一种两层前向型神经网络，包含一个具有径向基函数网络神经网络元的隐层和一个具有线性神经元的输出层。近些年，曹小涛[8]利用RBF神经网络对柔性机械臂进行了力/位置控制分析；谢晓竹[9]利用RBF神经网络对军用机器人进行鲁棒控制研究。本文利用MATLAB神经网络工具箱中的径向基函数网络来逼近柔性机械臂动力学方程，确定精确方程后即可得出理想轨迹，即输入数据θ直接求出驱动力矩。

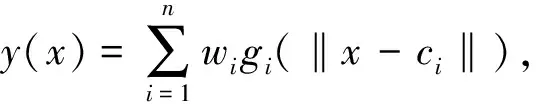
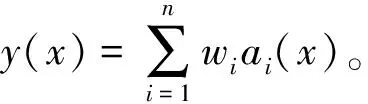
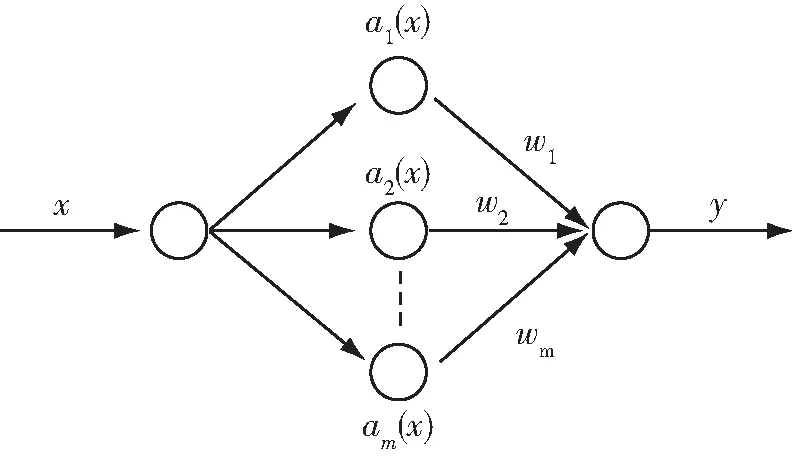
图6 径向基函数神经网络

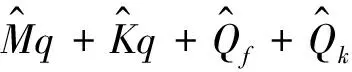
其中，αi(x)>0.05，0<β<1。

若使柔性机械臂的运动轨迹达到理想轨迹，可更新网络参数,使得t→时,

在设计径向基函数网络时有两种调用方法：newrbe和newrb。本文采用的是newrb函数设计网络，即每一次循环只产生一个神经元，可自动增加网络的隐层神经元数目，直到均方差满足精度要求。

SPREAD值的大小影响网络的预测精度，在这里分别在SPREAD=1、2、3、4的情况下计算网络的预报精度。分布密度为1时，网络的逼近误差比较小，故本文取SPREAD=1。

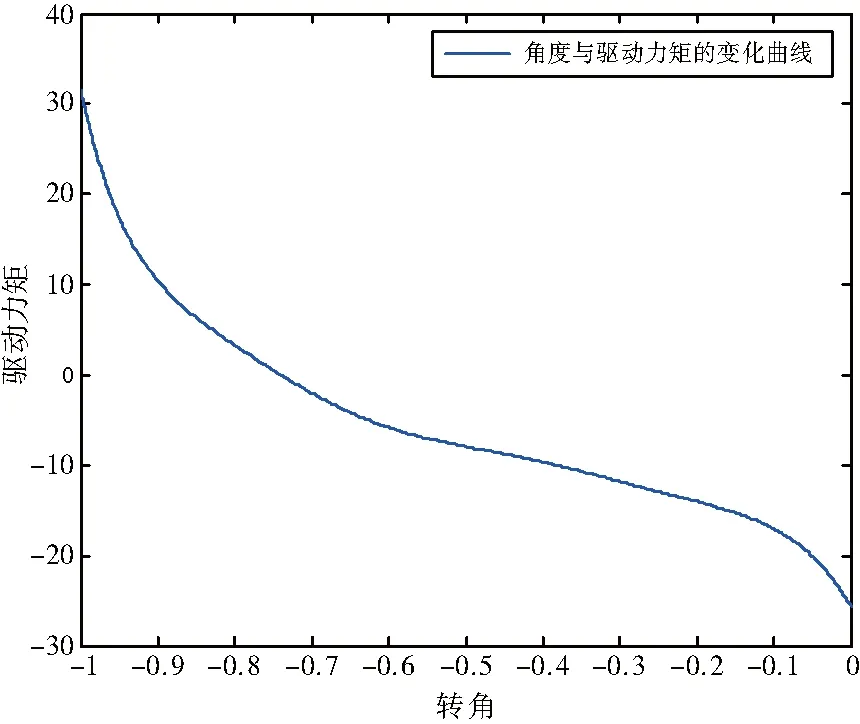
图7 利用RBF神经网络得到的转角θ与对应的驱动力矩关系曲线

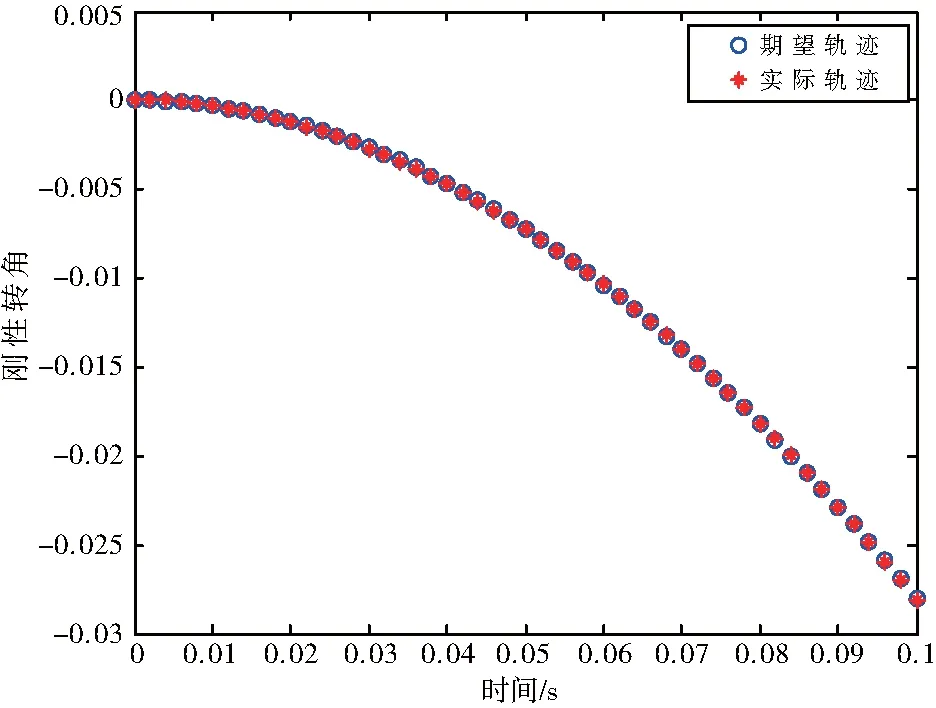
图8 转角θ的实际轨迹与理想轨迹的对比曲线

以近似方法得到的数据作为训练样本，利用RBF神经网络方法拟合系统方程，得到刚性转角θ和驱动力矩τ之间的关系，并根据理想轨迹预测出对应的驱动力矩(图7)。

为了验证RBF神经网络预测方法的准确性，将通过训练得到的数据作为初始值代入柔性机械臂的动力学方程中，得到机械臂的运动轨迹，与理想轨迹进行比较(图8)。

3 结果分析

本文采用的近似方法虽然不会造成轨迹的定性误差，但是由图5可知，柔性机械臂在运动过程产生的弹性变形，杆端产生的弹性振动会使最终得到的结果产生误差，致使结果不够精确，所以该方法已经不能满足现如今对柔性机械臂轨迹精度的要求。

由图8可知，本文所采用的RBF神经网络方法，可以较精确地得出作用在柔性机械臂上的驱动力矩，也能较好地预测出理想的运动轨迹，这是由于神经网络可以通过若干实例学习实现网络参数最优，而不需要被控对象的数学模型，也不需要事先为它设计好控制算法，并且神经网络对外界环境参数的变化具有一定的适应性。所以，RBF神经网络只要求给出符合柔性机械臂逆动力学方程的数据，就可以很好地拟合出驱动力矩与刚性转角之间的关系，并可以较好地预测出理想轨迹下的驱动力矩，并且能够降低编程工作量，误差小，直观方便。