基于FAHP方法的ZC管控能力影响因素分析研究

李少鹏 张益晨 陈建球

（1.通号城市轨道交通技术有限公司，北京 100070；2.北京磁浮交通发展有限公司，北京 100124；3.南宁学院交通学院，南宁 530299）

1 ZC系统简述

区域控制器（Zone Control，ZC）是基于无线列车运行控制系统（Communication Based Train Control System，CBTC）的关键地面设备，负责列车安全行驶，一条地铁线需布置多套ZC系统，ZC的管控范围过大会造成列车频繁降级运行，影响效率；ZC管控范围过小，会增加线路投资成本。本文使用模糊层次分析法（Fuzzy Analytic Hierarchy Process，FAHP）研究ZC的管控能力主要影响因素，以期合理的布置ZC。

2 FAHP对ZC管控能力因素的分析

2.1 改进FAHP方法评估步骤

结合ZC布置的具体特点及影响因素，通过FAHP方法进行适当的改进，进一步降低个人偏见带来的影响，提高评估结果的可信度。对影响ZC布置的因素评估分为以下的步骤。

1）确定ZC影响因素评估的总体目的，即确定最高层

2）根据最高层的目标，获取中间层的指标

影响ZC布置的因素较多，而且评估过程中的评估人员不需要具体关心这些因素之间错综复杂的关系。否则，就增加了他们的额外工作量，也给评估结果带来一定的误差，所以把最高层下的中间层再分为两层：决策层一和决策层二，这样做可以使影响因素之间关系更加直观，不至于错综复杂，给评估人员带来额外的影响。

3）采用模糊三角函数构建判断矩阵

设论域R上的模糊数M，则M的隶属度函数μM：R→[0,1]可以表示为：

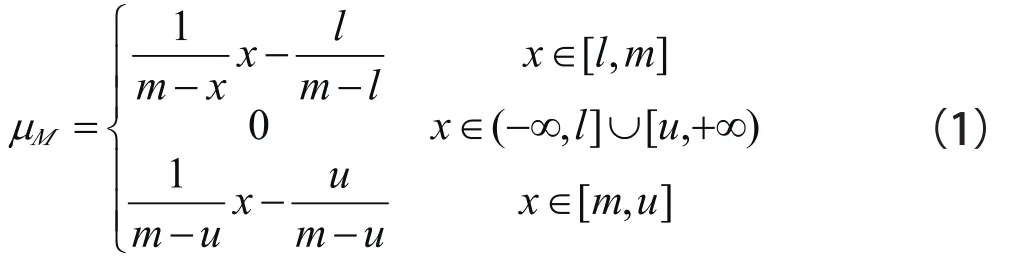
式中，l≤m≤u。l和u表示m的下界和上界值。m为M隶属度为1的中值。一般三角模糊数表示为(l,m,u)。

为了减少过多选择给评判带来的干扰影响，用三角模糊数M1,M3,M5,M7,M9代表AHP方法的1，3，5，7，9，而M2,M4,M6,M8代表是中间值。n位专家平均三角模糊数如下：

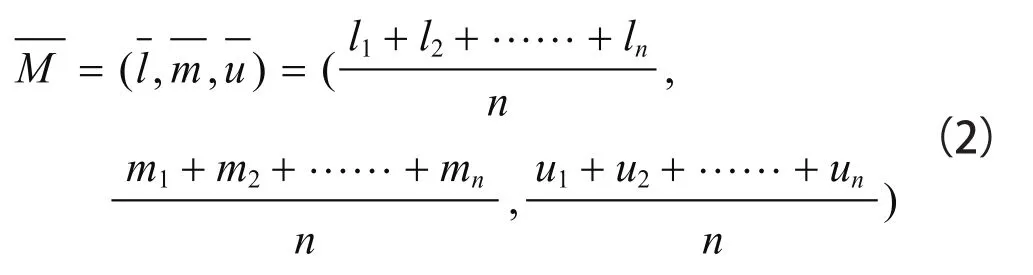
用专家三角模糊数可以构造得到三角模糊判断矩阵，根据这个三角模糊判断矩阵，根据公式（1）和公式（2）可计算判断矩阵，获得每一个影响因素的三角模糊权重向量。对影响因素权重值归一化处理。计算获得的影响因素权重值是非标准化的，没有办法进行统一的比较，所以需要对它们进行标准化处理，得到各指标的最终权重。将(a,b,c,d)标准化如下：

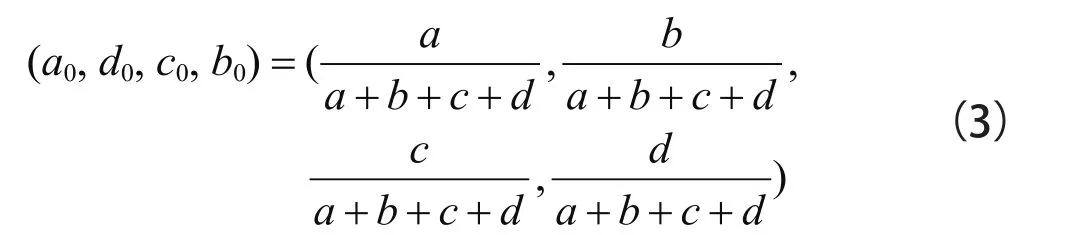
2.2 ZC布置的FAHP分析

2.2.1 ZC布置影响因素分析

虽然ZC的相关影响因素还没有一个统一说法，但由于其功能和结构与无线闭塞中心的相似，所以可以参考无线闭塞中心的布置因素，考虑控制能力、接口能力、维护适应性及效率。

1）ZC的控制能力

ZC的控制能力是影响ZC布局的主要因素。其指的是允许在单个ZC上注册的最大列车数量和其可以管辖的线路范围。

2）ZC的接口能力

ZC的接口能力需分析周期数据接口与非周期数据接口；ZC与列车的无线信道传输延时及ZC与地面设备的有线信道传输延时。

3）ZC的维护适应性

现在ZC结构普通采用的是二乘二取二的系统，当其中1套设备维修或者出现故障时，另1套备用设备可以正常的工作，基本不影响列车的正常运行，但考虑到维护方便性，ZC设备最好能集中设置；需要考虑的是扩建的可能性，有些车站由于作业量大，未来可能出现转线作业，这也需要在维护适应性中考虑到。

4）行车效率

城市轨道交通的一大特点就是运行密度大，发车间隔小，旅客人数众多，站台较小。如果是较低的行车效率，不仅会影响到旅客的满意度，在一些繁忙线路上还可能造成一定的危险。所以行车效率，也是ZC布置中必须要考虑的一个因素，其和无线信道的选择，列车的运行数量，ZC的布置数量等都有比较直接的关系。

2.2.2 ZC管控能力的FAHP模型

以控制能力、接口能力、维护适应性和行车效率作为网络层的簇，建立ZC布置的FAHP因素模型如图1所示。图1是进一步划分FAHP层次结构的依据。

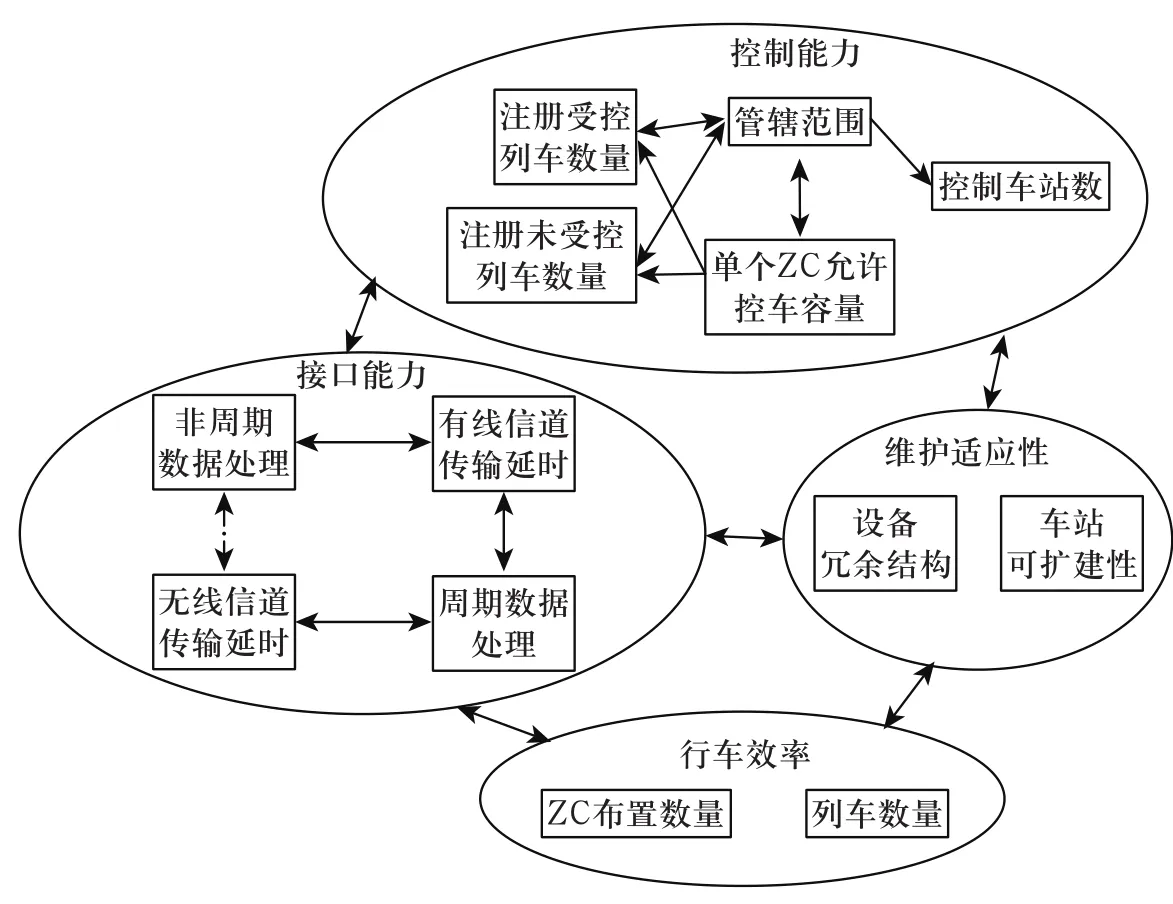
图1 ZC布置的评估因素模型Fig.1 Evaluation factors model of ZC layout

2.3 FAHP对ZC影响因素的排序

2.3.1 ZC评估因素层次划分

根据改进FAHP方法的步骤，可以确定ZC布置评估的目标层为ZC的布置影响因素排序。根据ZC管控能力FAHP模型，可以得到第一层的决策指标为：控制能力、接口能力、维护适用性和行车效率。根据以上分析的层次结构，评估ZC布置的划分如图2所示。

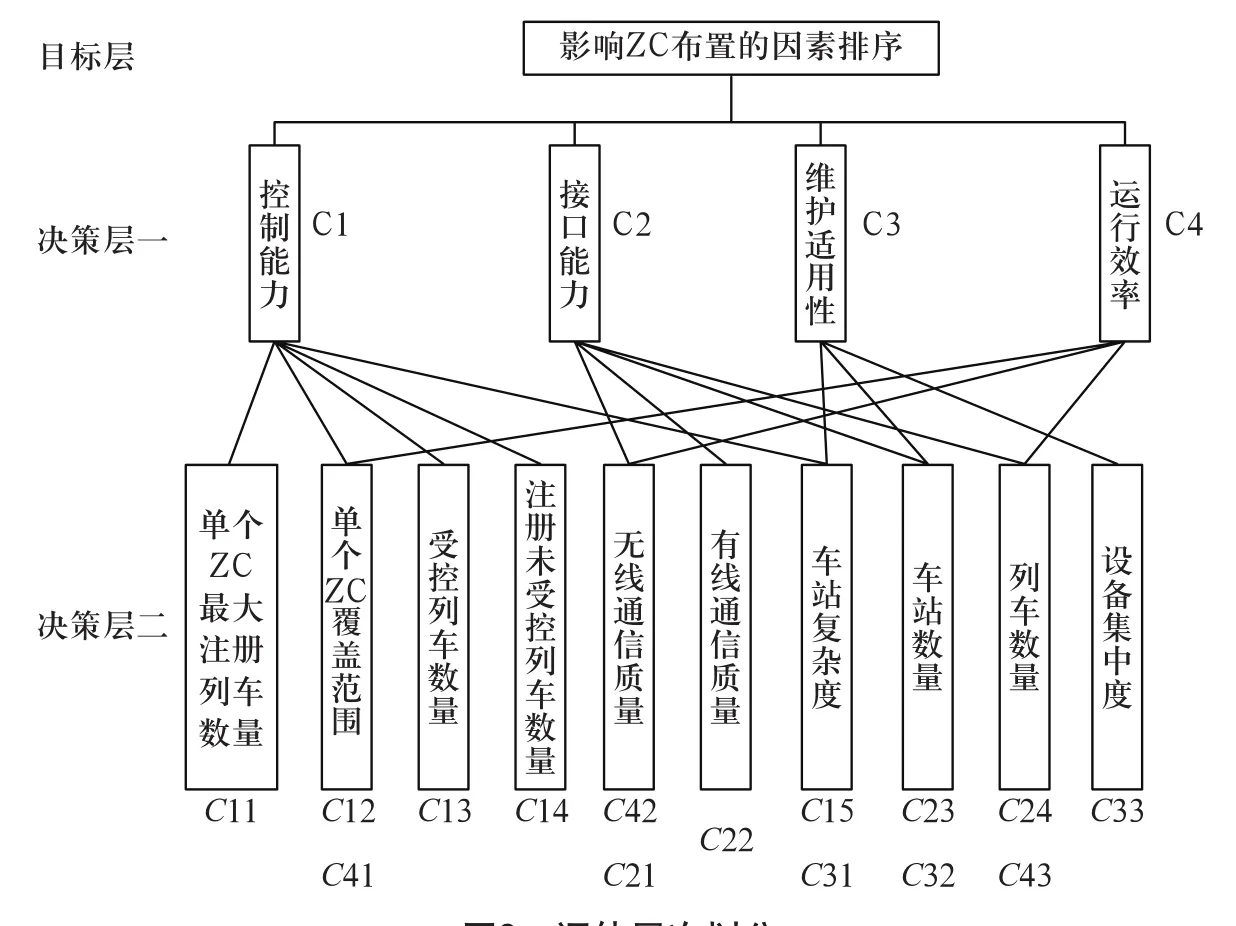
图2 评估层次划分Fig.2 Evaluation hierarchical division

2.3.2 评估因素判断矩阵构造

根据改进FAHP方法的描述，需要找3个CBTC系统的相关专家对图3的相关因素之间进行评分，获取三角模糊函数值。为防止专家之间知识层面的一致性，请的3个专家背景分别为：城市轨道交通控制系统CBTC的专家；ZC系统构建专家和通信领域专家。专家给出三角模糊数见表。评判标准依据表来进行，平均三角模糊数根据公式计算获得。表1是3位专家给出的三角模糊值。

表1中的C1与C2所对应的单元格表示控制能力和接口能力相比较，3位专家给出的值都是（1,1,1）。其他的依次类推，统一，可以获得决策层二的3位专家给出的三角模糊数值，如表2～5所示。

2.3.3 评估因素权重计算

根据表2可计算得到一级指标的权重值，得到一级指标的模糊一致判断矩阵如公式（4）所示。

再计算矩阵第一行的综合模糊值，即初始权值DC1。

DC1=（0.142 8,0.298 5,0.581 1）同理可得到DC2，DC3，DC4，如下：

DC2=（0.142 8，0.298 5，0.581 1）DC3=（0.090 2，0.263 6，0.653 7）DC4=（0.079 1，0.139 5，0.330 9）

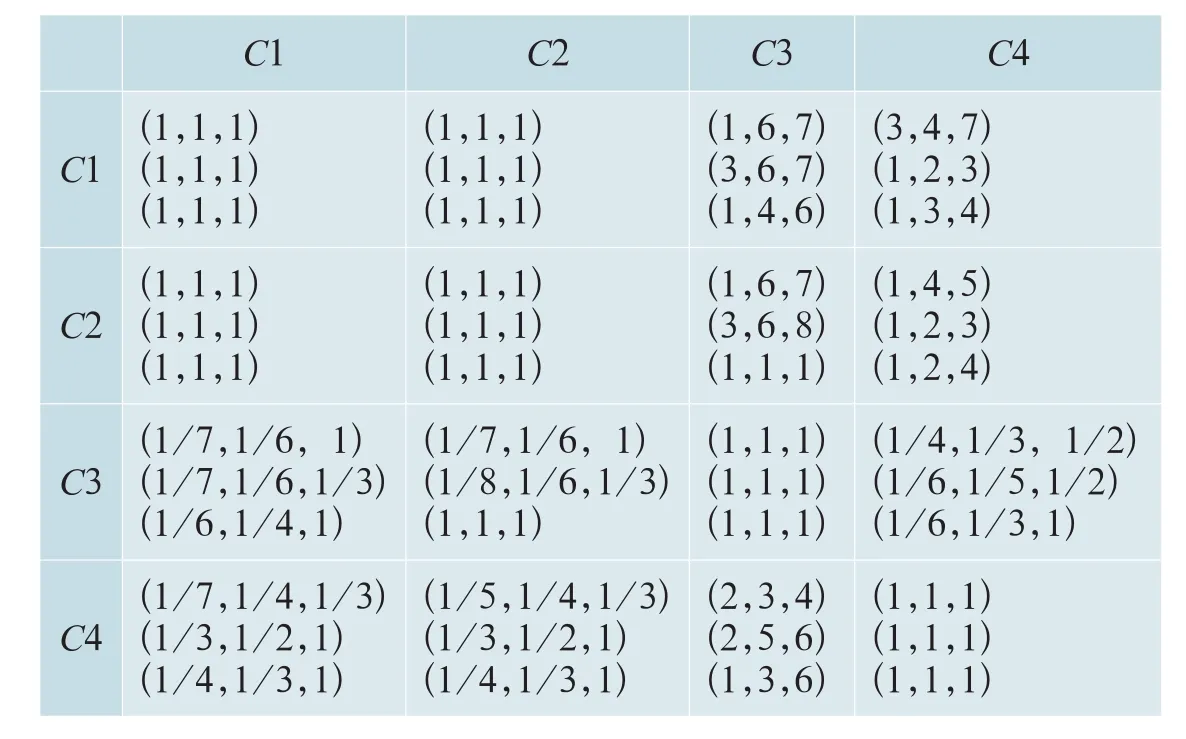
表1 一级指标的三角模糊判断矩阵DTab.1 Triangular fuzzy judgment matrix D of first-grade index

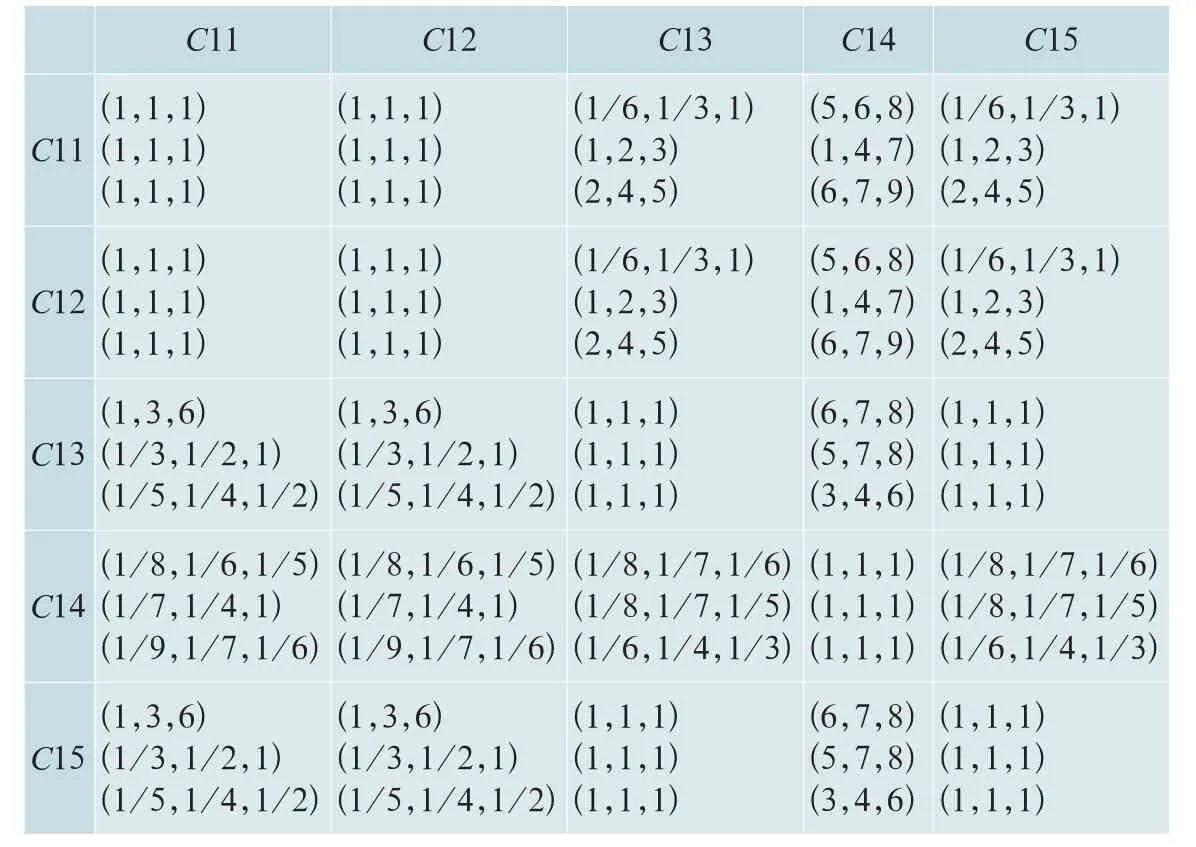
表2 二级指标C1判断矩阵D1Tab.2 Judgment matrix D1 of secondary-grade index C1

表3 二级指标C2判断矩阵D2Tab.3 Judgment matrix D2 of secondary-grade index C2

表4 二级指标C3判断矩阵D3Tab.4 Judgment matrix D3 of secondary-grade index C3

表5 二级指标C4判断矩阵D4Tab.5 Judgment matrix D4 of secondary-grade index C4

去模糊化处理：

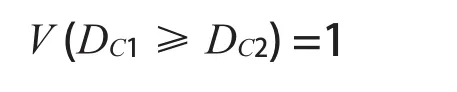
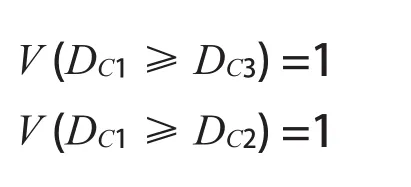
完成第一层的去模糊化处理，得：

d（C1）= minV（DC1≥ DC2，DC3，DC4）=min(1,1,1) =1

同理有：

d (C2)=1

d (C3)=0.935 4

d (C4)=0.534 8

根据公式（2）和公式（3），对一级指标进行权重值标准化，获取一级指标的最终权重：

(0.281 1,0.281 1,0.197 6,0.240 2)

根据以上步骤，可以得到二级指标的最终权重。

D1(0.217 0,0.217 4,0.234 7,0.105 8,0.225 1)

D2(0.168 4,0.168 4,0.331 6,0.331 6)

D3(0.461 2,0.402 1,0.136 7)

D4(0.270 3,0.297 4,0.432 4)

由于权重指标的最小值是0，最大值是1，所以权重指标置信域值可以设置为0.25。分别对每一位专家的模糊三角数进行去模糊化处理，再与以上的权重指标置信区间比较，发现没有超过置信域区间的专家数据，所以获得的影响因素权值指标为可信值。

得到影响ZC布置因素之间的权值分配如表6所示。

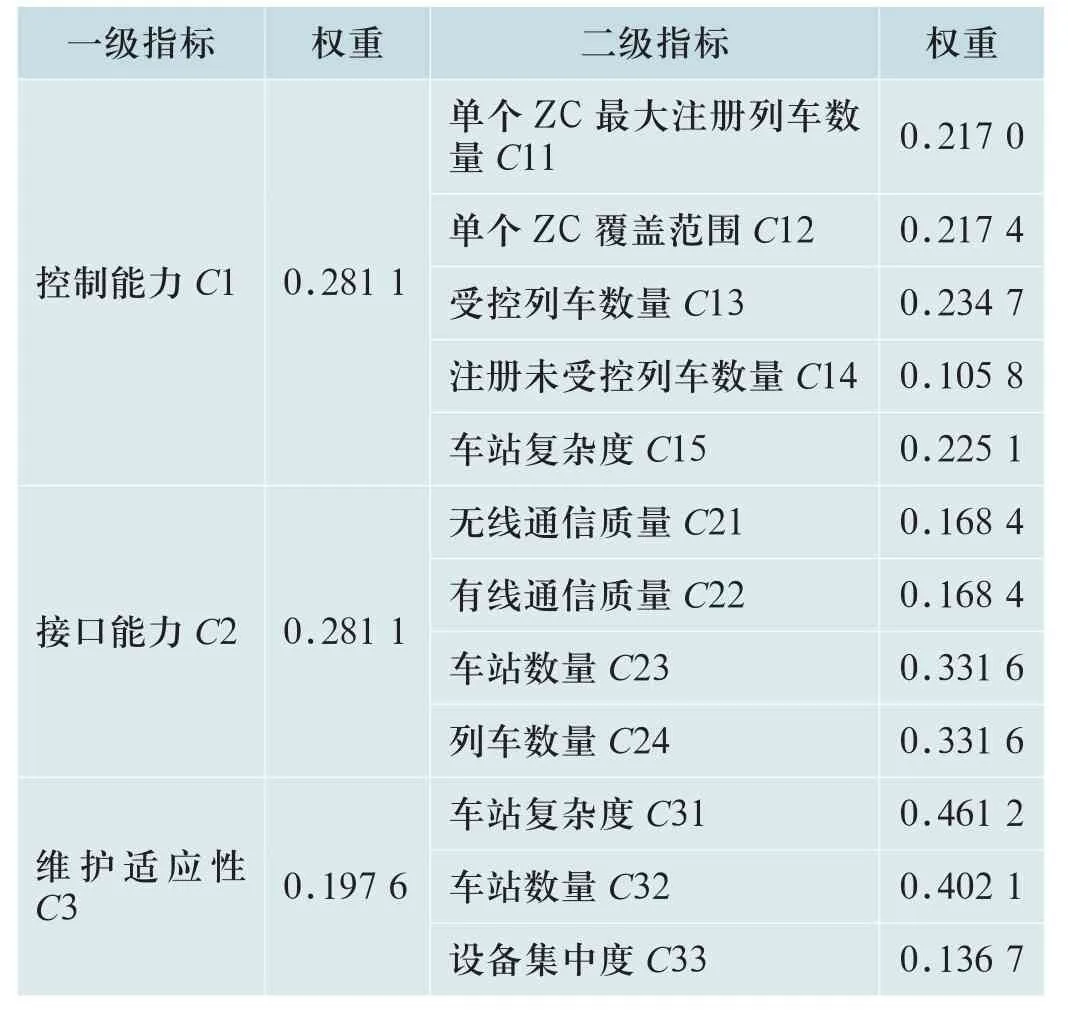
表6 影响因素指标权重Tab.6 Index weight of influencing factors

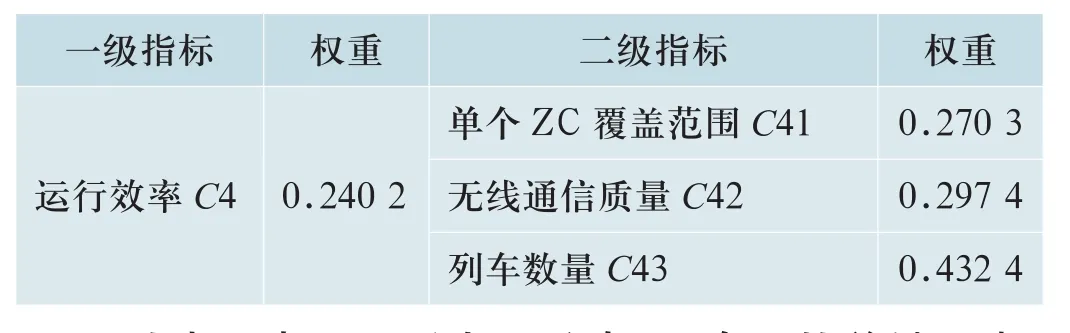
续表Continued

从表6中可以看出，影响ZC布置的关键因素排序为：控制能力、接口能力、运行效率、最后再到维护适应性。而二级指标中对ZC布置影响较大的有ZC车站复杂度、车站数量、控车容量、无线通信质量、单个ZC的受控列车数量等。实际在一条线路的ZC布置中要优先考虑这些关键因素。

3 小结

本文主要是通过FAHP算法对ZC管控能力因素的分析，首先介绍FAHP，并给出改进FAHP方法对ZC系统仿真可信性评估的步骤，接着进行ZC布置影响因素分析，找出影响ZC布置的各类因素，并根据这些因素建立ZC布置的FAHP因素模型，最后找到3个CBTC系统的相关专家对影响ZC布置的相关因素之间进行评分，获取三角模糊函数值，再利用Super Decisions仿真软件，通过FAHP算法得出各指标的权重，并对它们做出定量的全排序。