求解改进的基于布谷鸟算法的多目标优化问题

汪峰坤，张婷婷

（安徽机电职业技术学院 信息工程系，安徽 芜湖 241000）

多目标优化问题（multi-objective optimization problem，MOP）是工程和数学领域重要的研究方向。相对于单目标优化问题（single-objective optimization problem，SOP），多目标优化问题的解不是唯一的，且各解之间无法直接进行优劣性比较［1-3］。传统的MOP问题的求解方法有两种：一种是只搜索全局最优解，即在所有的目标函数上该解都是最优的，但当最优解不存在时，只能收敛到其中一个非最优解，并且很难扩大算法搜索空间。另一种是通过线性组合、目标加权、重要性排序等方法，将MOP问题转换为SOP问题，通过SOP算法进行求解，但存在需要额外的权值、目标优化不均衡、只能求出一个结果等问题。目前求解MOP问题，主要是求Pareto非劣最优解集，解集中的解都有自己的优缺点。

智能进化算法是一组模拟生物运动和自然规律的算法，它以适用问题类型多、鲁棒性好、参数少、收敛速度快及具有并行性等优点而在工程应用中被广泛使用，但也存在着理论基础薄弱、容易陷入次优解、搜索过程与结果不确定等缺点。常用的智能进化算法有：遗传算法、模拟退火算法、蚁群算法、离子群算法等。

布谷鸟算法（cuckoo search，CS）是一种模拟布谷鸟育雏特性的启发式智能算法［4-5］。杨新社等提出了针对 MOP 问题的布谷鸟优化算法（MOCS）［6］，相对于SOP问题的布谷鸟算法，他们主要修改的内容有：1）SOP中一次产生1个鸟巢作为问题的解；而MOP中一次产生n个鸟巢，每个鸟巢中有k个鸟蛋，k个鸟蛋对应k个目标函数。2）SOP中一次全局丢弃多个鸟巢，MOP中每个巢丢弃多个鸟蛋。MOCS对于目标函数较多时运行时间较长，效果不太好。

我们提出了改进的基于布谷鸟算法的多目标优化算法。改进后的算法支持求得指定个数S的Pareto非劣最优解，并提出了Pareto非劣最优解的选择方法：将可以扩大多样性的解直接加入解集，当解集中解的数量大于指定解个数S时，通过计算解方差，去除均匀性差的解，从而保证解集中解的数量不大于指定个数。

1 针对多目标优化的布谷鸟算法（MOCS）

多目标问题可描述为 F（x）=min［f1（x），f2（x），…，fn（x）］，其中 fn（x）是要优化的目标函数，n 为目标函数个数，决策向量。 F（x）是要使 fn（x）目标函数在决策向量上都取得最小值。在工程应用中，求得的最大值和求最小值是可以相互转换的。

MOCS 算法的流程如下［6-7］：

1）初始化鸟巢。随机生成n个鸟巢，为每个鸟巢随机生成k个鸟蛋（对应k个目标函数），共生成n×k个鸟蛋，并计算这些鸟巢的适应值。

2）判断是否满足结束条件。如果满足，则转到9）；不满足，则转到3）。

3）每个鸟巢都使用Lèvy飞行算法生成新的鸟巢。

4）计算所有新鸟巢的适应值。

5）循环判断当前所有鸟巢的Pareto非劣解。

6）每个鸟巢都以概率P随机丢弃，用偏好随机游动策略为丢弃鸟巢产生新解。

7）保留最好的解。

8）转到 2）。

9）输出最好解，算法结束。

在布谷鸟算法中，Lèvy飞行用来根据当前参数和值产生新鸟巢位置。新鸟巢位置计算公式是表示点乘运算。步长计算公式为常数［8］。

Lèvy飞行具有良好的局部搜索能力，为了扩大搜索范围，提高全局搜索能力,在布谷鸟算法中按照给定概率丢弃旧鸟巢，并且使用偏好随机游动策略产生新的鸟巢。计算公式是：其中p是概率值，表示t代的两个随机鸟巢。

2 Pareto非劣最优解集（Pareto front）

在多目标优化问题中，设向量 U＝［u1，u2，…，un］和V ＝［v1，v2， … ，vn］ 是 F （x） 的 两 个 解 。 如 果 满 足，则称解U优于解V。如果U中部分解优于解V，V中部分解优于解U，即时，无法直接比较解U和解V的优劣性，则称解U和解V互为非劣解。如果在F（x）的所有解中，没有比解U更优的解，则称U为F（x）的非劣最优解，也称为Pareto最优解［9］。对于多目标优化问题，我们求出的是所有非劣最优解的集合，称为Pareto前沿（Pareto front）。

3 评价标准

我们使用的解的评价指标为多样性指标和均匀性指标。

（1）多样性指标

（2）均匀性指标

4 改进算法

杨新社等提出的经典的MOCS算法是求出多目标函数所有的非劣最优解集，大部分多目标函数非劣最优解是无穷多个。当非劣最优解集较大时，算法运行速度较慢，所占内存较多，并且从工程的角度看，也无需求出所有非劣最优解集合。

针对经典MOCS算法的缺点，我们提出的改进的非劣最优解的筛选方法可以求出给定解的数量的非劣最优解集。

设当前非劣最优解集长度大于S，非劣最优解筛选规则如下：

1）如果当前解扩大了解集定义域的分布范围，则不删除；

2）如果删除当前解后解集的均匀程度提高最大，则删除。

计算非劣最优解均匀程度的方法是：首先对非劣最优解集按各维适应度降序排列，然后计算相邻节点的距离之和，通过均值计算出平均距离，通过方差公式计算相邻节点距离的方差值。方差越小，表示解分布越均匀。

改进后的MOCS算法流程如下：

1）初始化数据，随机生成n个鸟巢，计算这些鸟巢针对各个目标的适应值。

2）判断是否满足结束条件。如果满足，则转到9）；不满足，则转到3）。

3）根据鸟巢的各目标函数值进行判断，生成非劣最优解集。

4）针对非劣最优解集计算距离，按距离排序，保留前S个解。

5）使用Lèvy飞行生成新的鸟巢，计算新鸟巢的多目标解。按给定概率p随机丢弃鸟巢的解，用偏好随机游动策略产生新的解，计算新鸟巢的多目标解。

6）判断新鸟巢是否为非劣最优解，如果是则加入临时最优解集。

7）如果最优解集个数大于S，则根据非劣最优解筛选规则去除多余的解。

8）转到 2）。

9）输出非劣最优解集，算法结束。

5 改进MOCS算法仿真

我们选择了如下3个测试函数：

（1）SCH 函数

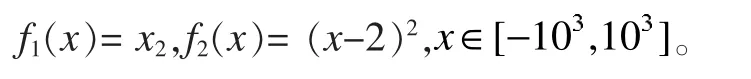
（2）MOP2 函数

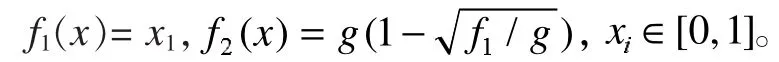
（3）MOP3 函数

f1（x）=1+（0.87-A1）2+（2.57-A2）2，f2（x）=（x+3）2+（y+1）2， 其 中 ， x, y ∈ [ 0,2]，A1=0.5sin x-2cos x+sin y-1.5cos y,A2=1.5sin x-cos x+2sin y-0.5cos y。

仿真实验参数设置为：鸟巢个数n=100，随机丢弃概率P=0.01，进化代数g=200，保留非劣最优解个数S=50。

求解的各测试函数的非劣最优解集的图形如图1、图2和图3所示。由图1、图2和图3可见：本算法可以生成指定个数的Pareto非劣最优解集，并且生成的解集分布比较均匀，效果较好。

各测试函数运行的多样性和均匀性指标值如表1所示。根据表1数据可知：本算法求得的三个测试函数多样性计算误差分别是0.04%、5.01%和4.17%，解的均匀性指标接近于零。

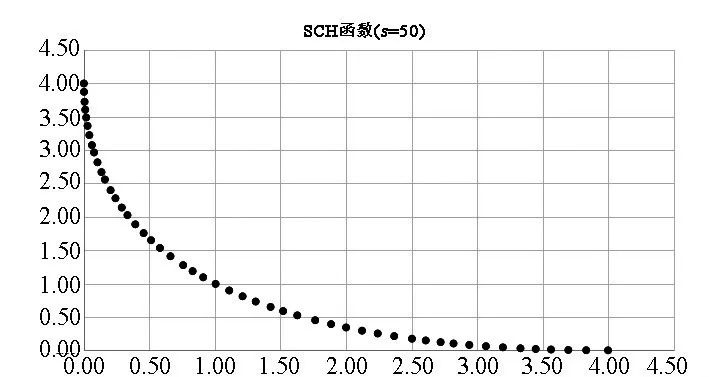
图1 SCH函数的Pareto非劣最优解集

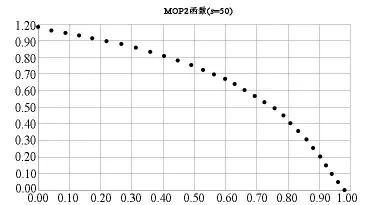
图2 MOP2函数的Pareto非劣最优解集

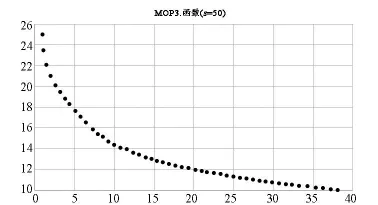
图3 MOP3函数的Pareto非劣最优解集

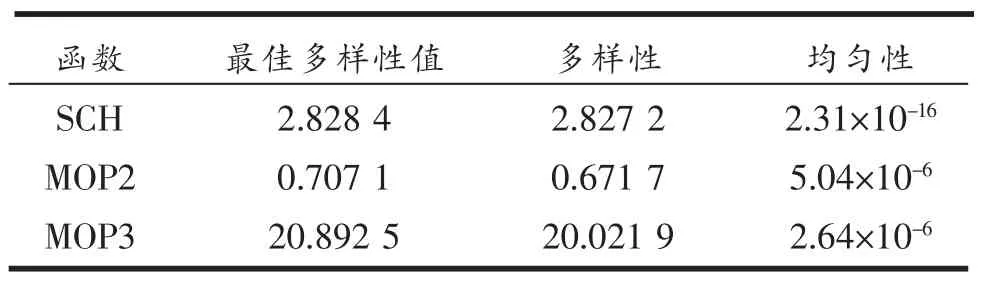
表1 测试函数多样性和均匀性指标值

相同进化代数、不同解集大小时的结果见表2。由表2可知，三个函数在解集大小不同时所求解的多样性均方差分别为0.12%、1.30%、0.69%，均匀性均方差分别为 3.65×10-15、8.73×10-6、1.13×10-5， 即本算法针对设置的不同解集大小所求出解集的多样性差距不大，均匀性也较好。

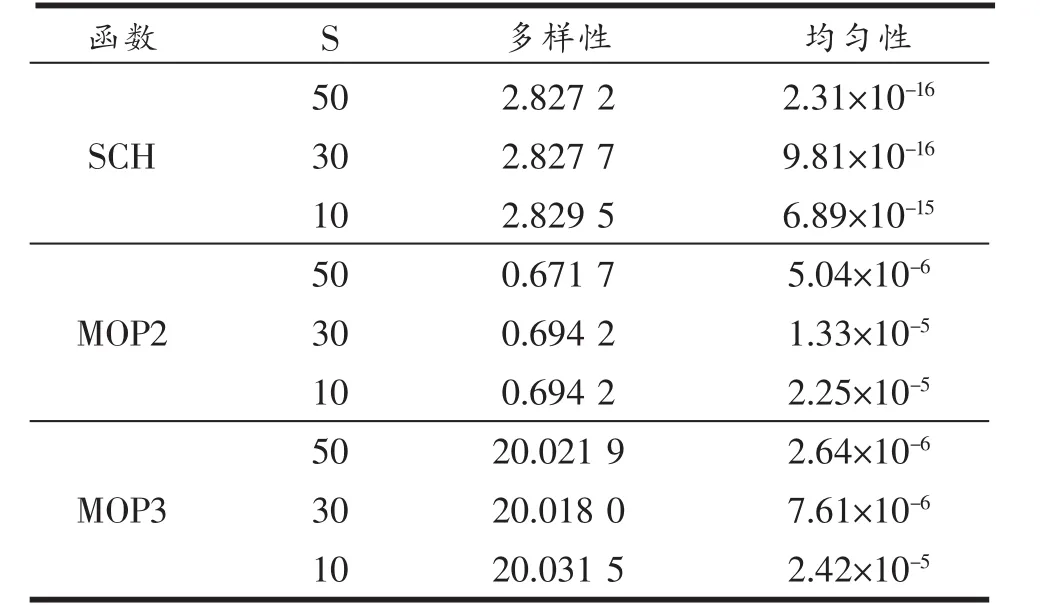
表2 测试函数在解集大小不同时的指标值

6 结束语

我们针对文献［7］中提出的MOCS算法进行了改进，改进的内容主要有：算法支持求解指定个数的Pareto非劣最优解，设计了非劣最优解的筛选淘汰方法。通过改进的非劣最优解的筛选淘汰方法，可以保证保留的解具有良好的多样性和均匀性。通过仿真实验验证，改进后的算法运行效果较好，所求解分布均匀，具有一定的工程实用价值。