各向异性网格上四阶抛物方程的收敛及外推

王云鹏

（新乡学院 数学与信息科学学院，河南 新乡453003）

传统的有限元方法要求区域 Ω 上的网格必须满足正则性假设或拟一致假设，即 hKρK≤ C或，其中， hK和 ρK分别是单元K的最大直径和内切圆的最大直径，Jh是区域 Ω 上的网格，C为与K无关的常数。如果Ω是窄边区域，采用传统的正则网格会使计算量变得非常大，而采用各向异性网格就可以通过较少的自由度得出理想的计算结果。在这种情况下，传统的Bramble-Hilbert引理已不再适用于插值误差分析［1-3］。T.Apel等［4］在各向异性网格上对Lagrange型协调元进行了误差分析，得出了一个判断单元是否具有各向异性特征的判定定理，但运用这个定理判断单元具有各向异性特征是比较困难的。陈绍春等［5］通过对该定理的改进得出了一个更容易操作的各向异性判定定理。 后来，陈绍春等［6-7］和石东洋等［8-10］通过对各向异性有限元的研究相继取得了一些有价值的科研成果。

四阶抛物方程［11-13］是有限元方法讨论的主要问题，对它的求解是有限元方法的重要内容，但所有的讨论都是在正则网格上进行的，而在各向异性网格上的研究还很少。在本文中，笔者把各向异性的ACM元用于四阶抛物方程，利用文献［12］提供的高精度分析方法，导出了半离散格式下的超逼近和超收敛结果，并在此基础上导出了更为精确的外推结果。

1 单元构造与各向异性特征

设Kˆ=[−1,1]2是 ξ -η平面上的参考元，中心为（0，0），四个顶点分别为aˆ1（− 1 ,− 1 ）, aˆ2（1,−1）, aˆ3（1,1）,

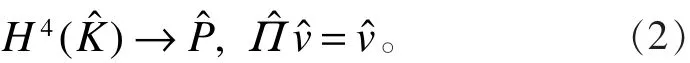
式中及以后出现的C为一个常数且与 hKρK无关，不同的地方取值可以不同。

3 各向异性超逼近结果

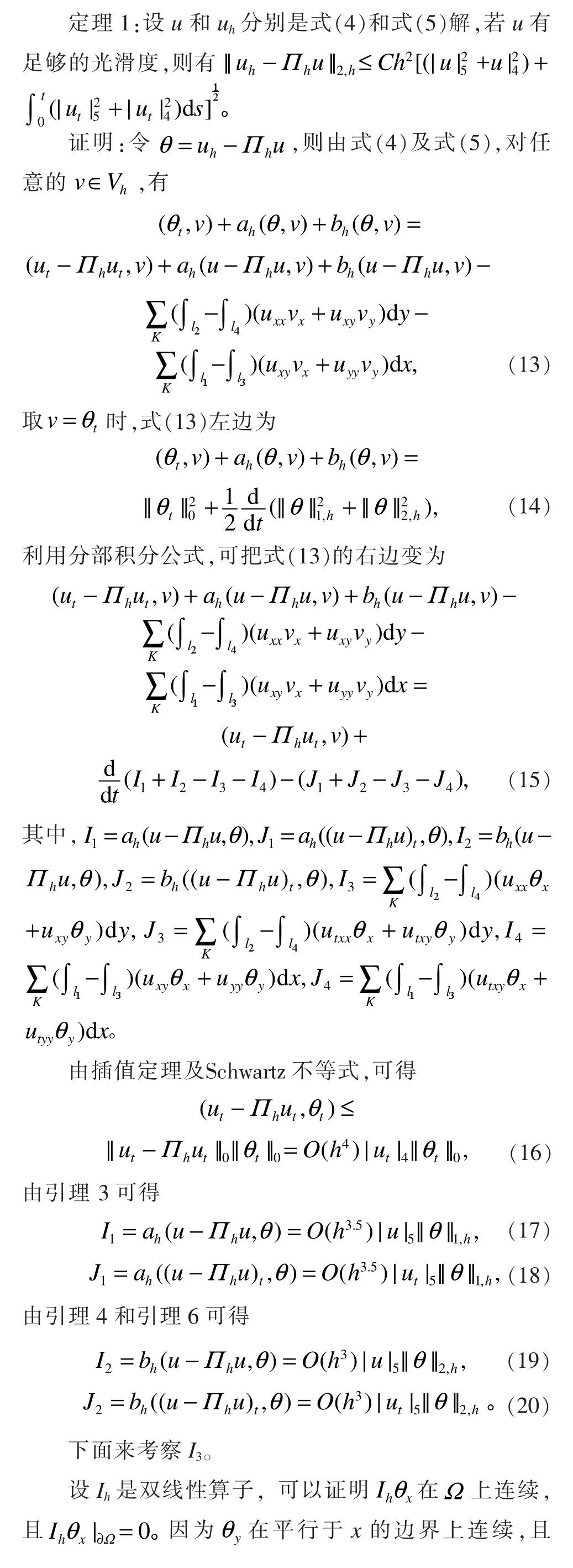
4 超收敛分析与外推

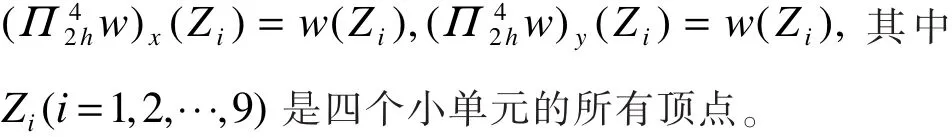
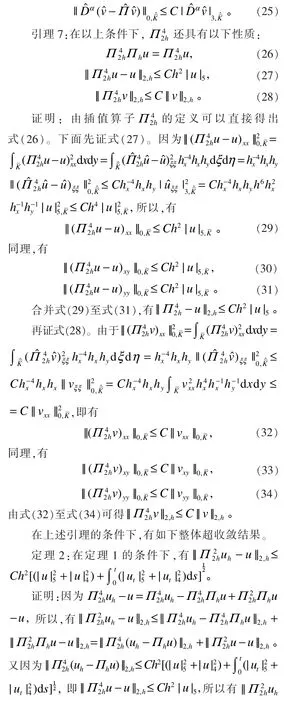
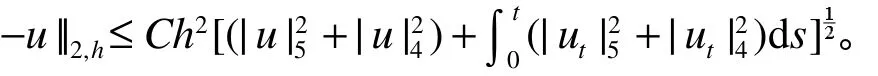
为了提高误差估计的精度，对方程的四阶项做外推处理。