基于神经网络的铁路路基沉降因素敏感度分析

李小娟,马红彬

(1.黄淮学院建筑工程学院,河南驻马店 463000； 2.河南承禹水利建筑工程有限公司,河南漯河 462000)

路基沉降通常由许多因素造成，主要包括断面几何参数、材料物理参数以及地基处理方式等[1-3]。在诸多沉降因素中，分析哪些因素最为关键，即分析沉降值对哪些因素最为敏感，对沉降的防治以及优化加固措施具有重要意义。

吴瑞麟[4]等基于FLAC对拓宽路基不均匀沉降进行了敏感度仿真分析；申永江等[5]通过有限元方法结合相对变化率公式，对高速铁路软土路基沉降因素进行了敏感度分析；Chen R P等[6]提出一种高速公路沉降因素敏感度分析的动态模型；以上敏感度分析方法虽然是基于不同的理论，但总体上均属于单因素逐次变化敏感度分析方法，这种方法可以直观反映出各因素对沉降的影响程度，但由于各因素之间量纲不一致且数量级差不同，因此不同因素敏感度计算结果可能差异巨大，不具有可比性；同时，这种方法实质上默认了路基沉降的影响因素之间是相互独立的，没有考虑到各因素之间的相互作用问题。

理想情况下，各因素对沉降的影响程度可通过建立各因素与沉降之间的显式函数模型，并以该函数因变量对各因子的一阶偏导计算得出，函数y=f(x1，x2，…，xn)，则xi(i=1，2，…，n)的关于y敏感度系数，即因子xi对输出y的影响程度Qi可定义如下

(1)

然而影响路基沉降的因素十分复杂，通常无法准确建立各因素与沉降量之间的显式函数关系。对此，本文提出一种基于均匀设计和神经网络的路基沉降因素敏感度分析方法。先以均匀试验设计的方法得出沉降量与沉降因素之间的样本数据，再根据BP网络建立路基沉降值与沉降因素之间的映射，从而可计算各沉降因素的敏感度系数，最终有效识别路基沉降的关键因素。由于在计算过程中采取了数据归一化处理，则有效避免了各因素量纲与数量级差异对计算结果造成的影响；同时，采用均匀设计与神经网络将各沉降因素置于一个统一的系统内进行分析，在分析时并不需要考虑各因素的相互作用问题。

1 计算模型及其沉降因素

1.1 计算模型

以蒙华铁路河南某段路基施工为例，路基顶宽8.8 m，路堤填高2.7 m；坡度h/l=1/1.5，采用土工格栅加筋。采用ANSYS软件建立的幅有限元模型如图1所示[7-8]，纵向计算30 m，采用4面体网格，共16 554 327个单元，岩土材料按弹塑性材料处理[9]。

图1 路基有限元模型

约束条件：地基底面竖直约束，地基外侧水平约束。

层间接触条件：完全连续接触。

1.2 沉降因素

根据文献[5]的归纳总结，路基沉降的影响因素主要包括：软土层厚度、软土弹性模量、泊松比、黏聚力、摩擦角、容重、路堤加筋层数，为表述方便，以上7个因素在本文中分别记为x1，x2，…，x7。为进行沉降因素敏感度分析试验，根据现场情况和室内试验得出各因素初值如表1所示。试验中各因素都是基于此初值进行变化的，变化幅度(试验步长)应取决于各因素的数量级与实际情况。

表1 各因素初值

在进行敏感度分析试验时，将各因素不同取值的组合代入有限元模型中，即可根据荷载情况计算出沉降量。

2 基于均匀设计的路基沉降试验设计

为获取敏感度分析的数据样本，需要进行一定数量的沉降分析试验。试验设计是一种在试验的范围内挑选代表性点的方法，试验点(样本)的选取需要具有代表性和分散性，本文采用均匀设计[10-11]法设计沉降试验。

均匀设计法最早由中国数学家王元与方开泰于1978年提出，是数论方法中的“伪蒙特卡洛方法”的一个应用。均匀设计试验点代表性和分散性良好，且需要进行的试验次数较少，能够极大减轻试验工作量，尤其针对类似本文的多因素试验设计问题，均匀设计比之其他试验设计方法更为适用。

由于均匀设计不需要考虑各因素之间的相互作用，并可以最少次数的试验获得最全面的试验信息，可用于多参数非线性模型的试验估计，非常适合岩土力学领域问题的分析。

2.1均匀设计表

均匀设计的核心问题是均匀设计表的构造，均匀设计表的通用符号为Un(qs)，其中，U是均匀设计的代号；n=q，前者代表总共需要的试验的数量，后者代表试验水平数量；s代表该均匀设计表所包含的因素的数目。

那么，对于本文7个因素，试验水平数一般不少于试验因素数，水平数取10，为了方便计算赋值，式(2)以矩阵的形式给出了U10(107)的均匀设计表。

(2)

2.2 均匀试验

结合各沉降因素的初值(表1)，根据每个因素的初值情况，将该因素取等步长的10个值作为试验水平。

现以因素1和因素3为例作具体说明：因素1软土层厚度初值为10 m，将此初值作为一个水平，在此基础上逐次增加1 m，每增加一次作为一个新的水平，直至15 m；再在10 m的基础上逐次减少1 m，每减少一次作为一个新的水平，直至6 m，共取得10个水平，依次为6，7，…，15 m。因素3泊松比的初值为0.32，将此初值作为一个水平，在此基础上逐次增加0.01，每增加一次作为一个新的水平，直至0.37；再在0.32的基础上逐次减少0.01，每减少一次作为一个新的水平，直至0.28，共取得10个水平，依次为0.28，0.29，…，0.37。其他因素10个水平的取值以此类推，如表2所示。

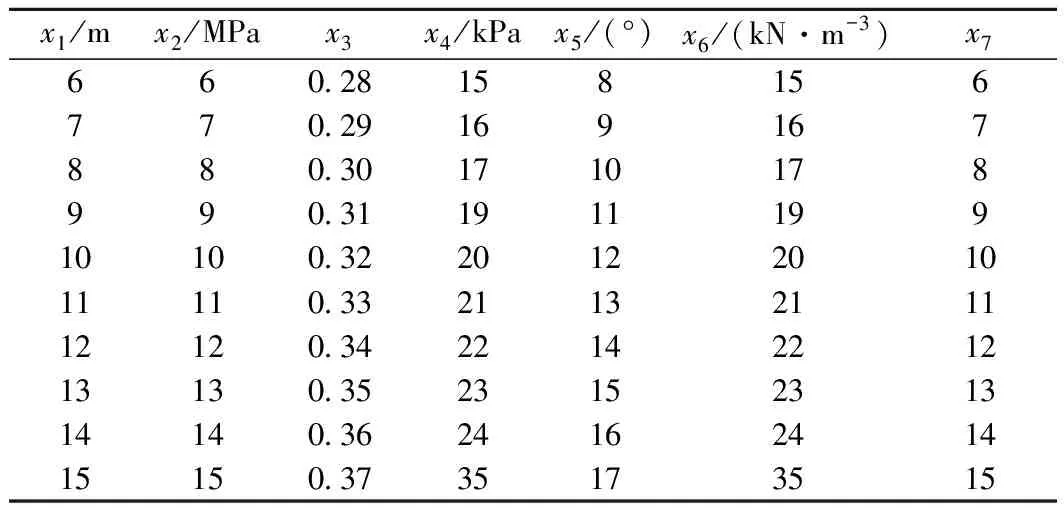
表2 各因素水平

根据表2，对于本文的7个沉降因素，可以表2中的数据设计均匀试验。其具体涵义为：表2中，第1个因素的10个水平按式(2)第1列排序，第二个因素的10个水平按照式(2)第2列排序，……，第7个因素的10个水平按式(2)第7列排序。排序之后，按每一行各因素水平的组合，形成相应的工况，代入有限元模型，并以相同荷载状况计算沉降量。

实际计算中，路基荷载为静荷载+动荷载。由于本文工程实例中蒙华铁路属于重载铁路，不宜简单地将静荷载和动荷载一并简化为静荷载处理。参照大秦线实测动应力[12]，本文动荷载取路基面上平均动应力荷载为60 kPa。静荷载包括轨道荷载和列车荷载，计算所需参数包括设计轴重，钢轨、轨枕型号，道砟厚度，砟肩宽度等，具体参考国家铁路局《重载铁路设计规范》(TB 10625—2017)[13]，静荷载的具体计算方法参考文献[14]。

任取一行因素水平的组合，例如表2第9组，根据平均动应力荷载和相应工况下的静荷载，采用ANSYS计算路基最终沉降，如图2所示。

图2 路基沉降的有限元计算

同样地，其他各组参数组合的最终沉降结果均由ANSYS软件在特定荷载下，按第9组路基沉降的方法，通过有限元模型计算得出。如表3所示，可得到路基沉降因素敏感度分析的初步数据样本。

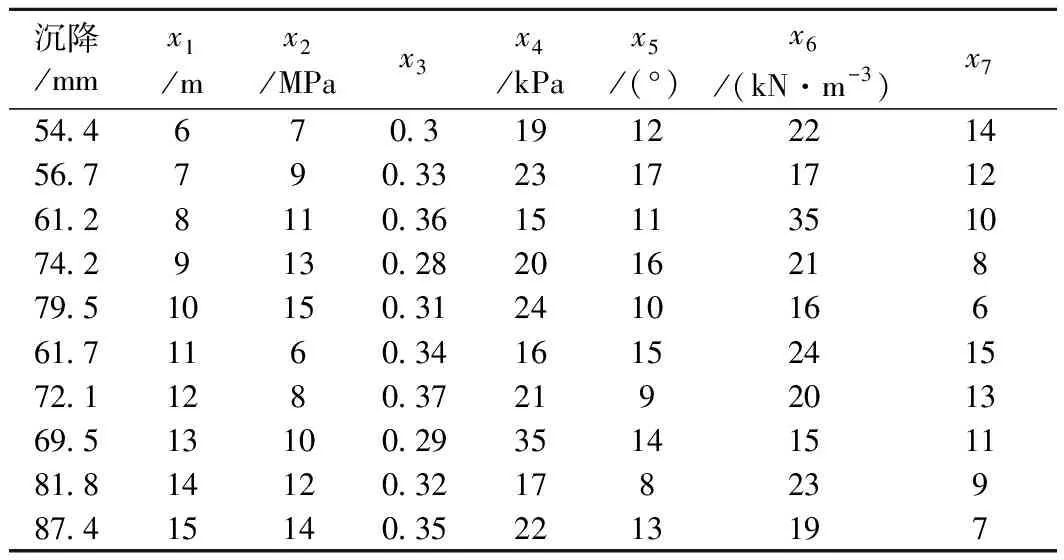
表3 试验结果

2.3 数据预处理

由于本文各因素的量纲不同，数值上差异较大，为避免信息缺失，在使用数据之前，需要将所有数据样本按公式(3)进行归一化处理。

(3)

式中，Y和X分别代表每组因素归一化后和归一化前的值，maxX和minX分别代表每组因素中最大值和最小值。经过归一化后的数据全部在[0.1，0.9]区间范围内，可保全数据相对信息且便于计算。

然后，可以归一化后的数据为样本数据进行BP神经网络训练，从而建立路基沉降与各因素之间的映射关系，以便进行敏感度分析。

3 基于神经网络的沉降因素敏感度分析

为分析路基沉降各个因素对最终沉降值的影响程度，需建立各因素与沉降之间的映射关系，并基于该映射进行敏感度分析。人工神经网络[15-19]可以模仿人脑中大量神经元互相连接、并行信息的处理方式，通过对一定数量数据样本的学习，可建立自变量与因变量之间的多参数、非线性映射。理论上，3层及其以上的神经网络能满足任意映射或拟合问题。以下以表3所示的数据作为训练样本并归一化，并以神经网络建立沉降量与各个因素之间的映射，然后从神经网络中提取出输入层到隐含层、隐含层到输出层之间的权值，继而以权积法进行各误差因素的敏感度分析计算。

3.1 基于神经网络的敏感度系数计算(图3)

图3 BP网络及算法中的变量符号

训练集D={(x1，y1)，(x1，y2)，…，(xm，ym)}，xi∈Rd，yi∈Rl，即输入层包含d个因子，输出l维实值向量。本文以图3描述神经网络的基本架构，该网络输入、输出、隐含层包含的神经元数目分别为d、l和q。

其中，vih代表输入层第i个神经元与隐含层第h个神经元之间的连接权，whj代表隐含层第h个神经元与输出层第j个神经元之间的连接权；同时定义θj代表输出层第j个神经元的阈值，γh代表隐含层第h个神经元的阈值。

隐含层和输出层的神经元都采用如公式(4)所示的Sigmoid函数

(4)

(5)

则该网络在(xk，yk)上的均方误差为

(6)

图3的网络中有q(d+l+1)+l个参数需要确定，任意参数v的迭代更新式为

v←v+Δv

(7)

那么对于各参数根据式(4)～式(7)可推导出

Δwhj=ηgjbh

(8)

Δvih=ηehxi

(9)

Δγh=-ηeh

(10)

Δθj=-ηgj

(11)

其中，gi为输出层神经元的梯度项；eh为隐含层神经元的梯度项，其计算公式为

(12)

(13)

η∈(0，1)为学习速率。

隐含层神经元的数量q采用公式(14)近似计算，其中a为[1，10]之间的任意正整数。

(14)

BP神经网络的计算流程如表4所示，该算法实质上是建立了一种输入层和输出层之间的映射关系，那么可以根据这种映射关系求解输入层各个因子对输出层的影响程度，即求解输入层各个因子的敏感度系数。权积法是一种针对于BP网络利用输出网络各层之间的连接权进行敏感度系数计算的方法，第i个输入因子xi对第j个输出因子y的影响程度(敏感度系数)Qi为

(15)

当输出因子只有1个时，例如本文映射关系只存1个输出因子即沉降值，f′(netk)=1，具体推导过程详见文献[20]。

表4 BP神经网络的计算流程

注：初始参数的选择仅与神经网络的收敛速度有关，而与最终输出网络的优劣无关，由于本文训练样本不大，收敛速度对计算结果几乎无影响，故对初始参数的选取不做详细研究，仅在(0，1)范围内随机选择。

3.2 沉降影响因素的敏感度计算

根据3.1节中的理论，可建立各因素和的映射关系。

在数据归一化的基础上，将误差因素作为神经网络的输入神经元，误差结果作为输出神经元，那么BP神经网络输入层单元数d=7，输出层单元数d=1，a取7，根据式(14)计算出隐含层单元数q为10；训练过程中，将表3中数据归一化，以前9行数据作为训练集，后1行数据作为测试集。为避免BP网络过拟合(即训练误差持续下降，测试误差却有可能上升)，将训练集用来计算梯度、更新连接权和阈值，测试集用来估计误差，若训练集误差降低但测试集误差升高，则达到停止条件，同时返回具有最小测试集误差的连接权和阈值。

当训练停止时，则误差因素与测量误差之间的非线性映射关系已建立，根据输出网络各神经元之间的连接权值，以公式(15)计算各输入神经元的敏感度系数。由此，可获得沉降对各内部因素的敏感度系数，结果如图4和表5所示。

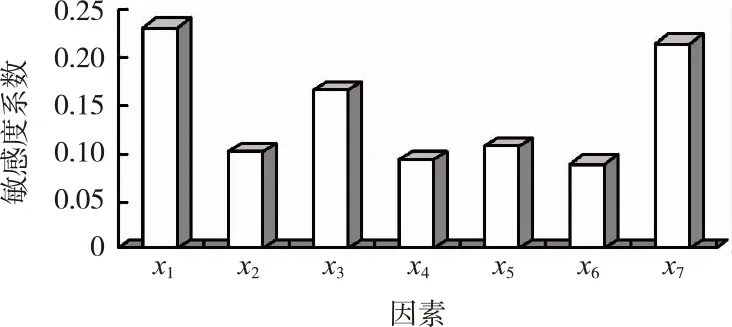
图4 沉降因素敏感度分析

因素敏感度系数x10.231x20.102x30.165x40.092x50.107x60.089x70.214

由图4和表5可知，上述7项沉降因素中，软土层厚度、路堤加筋层数这2项因素的敏感度系数分别为0.231和0.214，高于其他因素，说明这2项因素对路基沉降的影响程度比其他因素要高，若需要有效控制沉降，则该两项因素在施工过程中需要被着重考虑。其他因素对沉降的影响程度要弱于上述2项因素。

4 结论

本文将均匀试验设计、人工神经网络理论与方法引入到路基沉降因素敏感度分析这一领域，采用BP神经网络结合均匀设计求解了各个沉降因素的敏感度系数，用以衡量各沉降因素对路基沉降的影响程度。

(1)在明确了路基7项主要沉降因素和参数的基础上，通过均匀设计方法设计了敏感度分析试验，通过试验得出了敏感度分析的样本数据。

(2)以样本数据，根据BP网络建立了沉降值与沉降因素之间的非线性函数映射，再以神经网络各隐含层之间的权值计算各沉降因素的敏感度系数，确定了各沉降因素对最终沉降结果的影响程度。

(3)软土层厚度、路堤加筋层数对沉降值的影响程度高于其他因素，此敏感度分析结果可为施工中路基沉降控制提供依据。