轨道交通微型隔振桩隔振效果简化预报模型

刘晶磊,王奥运,仉 健,于川情,刘 桓

(1.河北省土木工程诊断、改造与抗灾重点实验室,河北张家口 075000； 2.河北建筑工程学院土木工程学院,河北张家口 075000)

高速铁路、城市地铁等轨道交通作为快速的交通方式得到迅速的发展，但是由于轮轨与轨道接触面的不平顺在地表造成了一系列的振动，对邻近建筑物的结构安全和人们正常生活造成较大影响[1-5]。国内外学者为降低振动带来的影响而做出了不懈努力。Murillo C等[6]研究表明表面波在列车振动中占据主要地位，阻断其在土中的传播路径可以有效减少振动对周围环境的影响。Woods[7]提出将空沟作为隔振屏障，从机理上分析沟深与振动波波长对隔振效果的影响，为空沟作为隔振措施提供了参考。张雷刚等[8-9]采用数值分析得出高速铁路空沟后侧土体的振动规律，空沟的沟深对隔振效果影响显著，沟宽对隔振效果影响不明显。冯青松等[10-11]针对振动响应问题，提出了一系列适用于振动响应的理论计算模型，并结合现场实测验证了模型的可靠性。王启云等[11-15]采用模型试验及现场测试对列车运行时的路基振动特性进行了研究。陈洪运等[16-18]通过模型试验研究微型单排排桩的隔振效果，分析出单桩截面尺寸对隔振效果影响不明显，桩长度、桩间距对隔振效果影响显著。

基于以上对振动特性的研究和不同隔振措施几何参数的模型试验研究，以探究位于地表浅层中的微型混凝土单排隔振桩的隔振效果。主要考虑微型隔振桩的桩长、桩间距、振源距、桩截面宽度4个几何参数作为敏感因素，试验结果采用振幅降低比Ar[7]表示微型单排隔振桩隔振效果，以此建立微型单排隔振桩的隔振效果简化预报模型并分析其敏感因素。

1 试验准备

1.1 试验场地安排

试验采用3 m(长)×2(宽) m×1.5 m(深)的砂坑，放置砂土于坑内，每填放5 cm厚土体后进行人工夯实。其中砂土的物理指标有：粒径d<5 mm，含水率w在9%～10%，密度ρ为1 800～1 900 kg/m3。试验采用WS-Z30型振动台控制系统，设备主要包括数据采集控制仪、功率放大器、电荷放大器、激振器、信号发生器、加速度计放大器、加速度传感器(灵敏度为4PC/ms-2，频率响应为0.2～8 000 Hz，测量范围为50 m/s2，质量28.5 g)。试验中所使用的微型隔振桩截面设计为正方形，桩长0.2～1.0 m，桩截面宽0.10～0.25 m，采用混凝土浇筑。试验中加速度传感器，微型隔振桩、激振器布置如图1所示。

在试验中，采样频率为5 000次/s，采样时间为3 s，在此期间电荷放大器数值要保持一致。激振器采用实测铁路某重载铁路线、测试车型C80(满载)重车车速67.4 km/h试验信号进行激振，每测试完一组工况，及时记录数据。

图1 隔振桩及加速度传感器布置

1.2 评价指标

微型混凝土单排隔振桩的隔振效果，通过振幅降低比实测值Ar表示，振幅降低比越小，表示隔振效果越好[7]。Ar定义如式(1)所示

Ar=a1/ao

(1)

式中a1——设置微型隔振桩后的地表竖向振动加速度值；

ao——自由地基激振时同一位置地表竖向振动加速度值。

同时定义微型隔振桩的桩长为α1，相邻隔振桩最近外边缘间距为α2，隔振桩到振源的距离为α3，隔振桩截面宽度为α4，作为辅助评价微型单排隔振桩隔振效果的参数。

2 试验方案设计

βi=(αi-α0i)/Δi，Δi=(α2i-α1i)/γ

(2)

式中，βi为量纲为1的量；[α1i，α2i]为第i个试验因素的变化范围；α0i为第i个试验因素的上下界平均值；Δi为第i个试验因素的变化范围；根据二次回归正交设计确定γ=1.414。

在多因素隔振试验中采用4个影响因素，每个影响因素取5个水平，则需设置25组试验。考桩桩截面宽度对隔振效果影响不明显，桩长度、桩间距对隔振效果影响显著[16-18]、微型隔振桩与振源相对位置设定规则[7]，结合场地条件由回归正交试验设计计算出因素水平，取值情况见表1。

表1 试验因素水平

3 多因素作用下的试验结果及预报模型

3.1 多因素作用下的振幅降低比预报模型

(3)

式中βi——一次项的中心变化项的编码因素；

βkβi——一次交互项的中心变化项的编码因素；

bo、bi、bki、bii——与之对应的回归系数。

(4)

式中p——试验影响因素，取值4；

n——试验组数目，n取值25；

γ=1.414。

地表竖向振动加速度值如表2所示。

二次回归正交试验设计计算如表3所示。

表2 地表竖向振动加速度值

注：a1为设置微型隔振桩后的地表竖向振动加速度值；ao为自由地基激振时同一位置地表竖向振动加速度值。

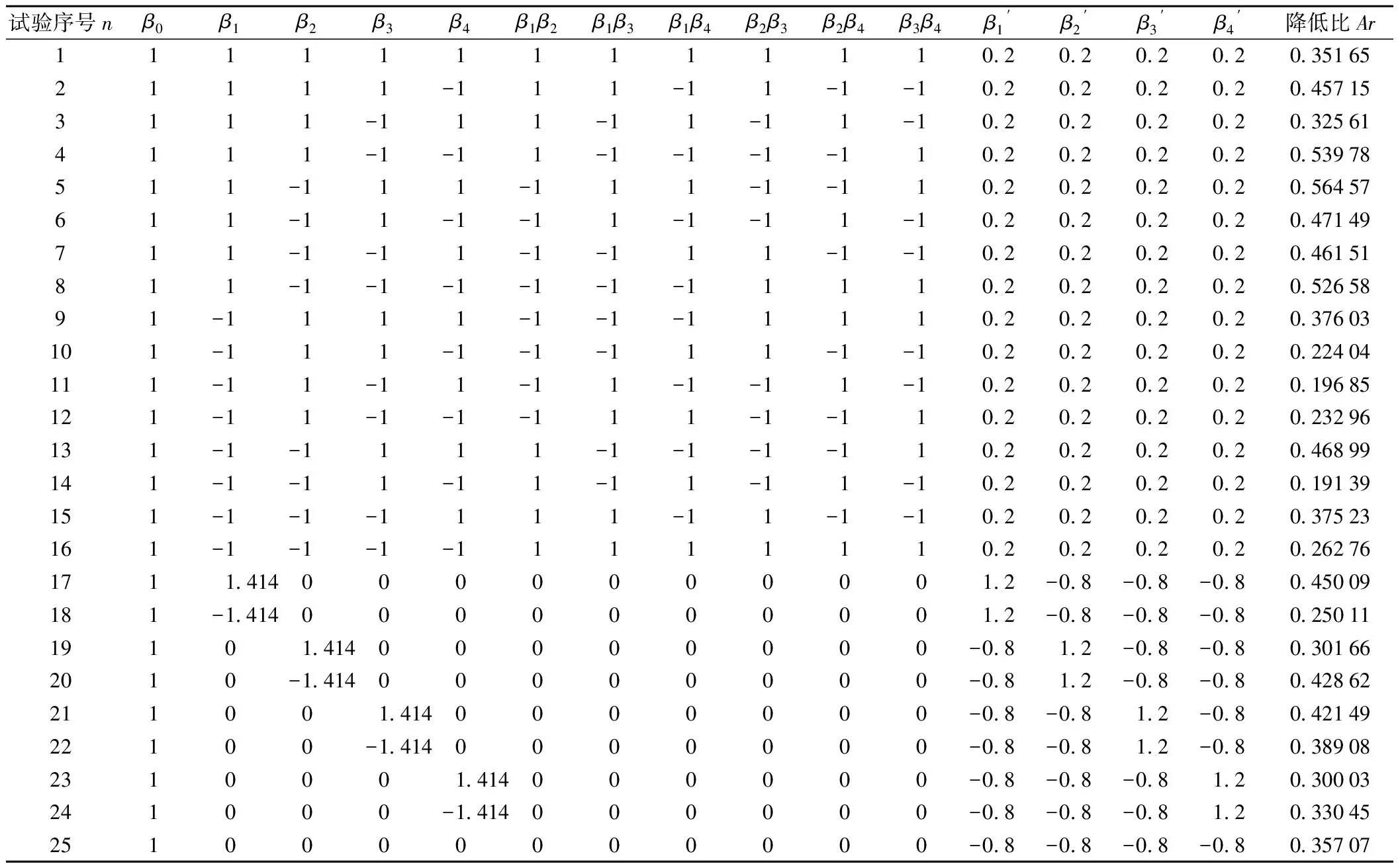
表3 二次回归正交试验设计计算

结合表3由二次回归正交设计原理，可得微型单排隔振桩的振幅降低比回归方程为

0.009β4-0.005β1β2-0.013β1β3-0.050β1β4+

(5)

式中R2——复相关系数。

对回归方程(5)进行显著性检验，当取显著性水平α=0.05，由F分布表[21]查得F0.05(14，10)=2.87，F0.05(1，10)=4.96，其二次回归方差分析见表4。

表4 二次回归方差分析

3.2 振幅降低比预报模型的简化修正

由试验的正交特性可知，当回归系数无关时，可以直接删去该变量，同时不影响其他变量的回归系数[19-20]。从而可以得修正回归方程如下

(6)

对回归方程(6)进行显著性检验，当取显著性水平α=0.05，由F分布表[21]查得F0.05(6，18)=2.61，F0.05(1，18)=4.45，其二次回归方差分析情况见表5。

表5 二次回归方差分析

3.3 回归系数修正对回归方程显著性影响分析

构造统计量S对方差分析后删去无关变量后，对回归方程显著性影响情况进行判别，统计量F的定义如下

(7)

式中R1、R2——回归方程(5)、(6)的复相关系数；

k1、k2——回归方程(5)、(6)的自变量个数；

S——服从自由度k1-k2和n-k2-1的F分布。

对式(7)代入各已知量得F=1.563

由因素水平编码公式(3)、公式(4)对回归方程(6)处理后，可得振幅降低比实际值Ar的方程式

Ar=0.147+1.788α1+0.347α2-0.359α3+

1.045α4-4.132α1α4-2.533α2α4+1.477α3α4+

R2=0.937

(8)

对试验所得振幅降低比实际值与回归方程计算预测值进行误差分析，各组试验实际值与预测值的相对误差ε如图2所示。

图2 隔振桩振幅降低比实际值与预测值的相对误差比较

从图2可知：振幅降低比试验实际值与回归方程计算预测值最大相对误差出现在第3组试验，相对误差值9.97%，误差值较小，可知微型隔振桩振幅降低比预报方程模型式(8)是可靠的。

4 影响隔振桩隔振效果的敏感因素权重分析

通过对微型隔振桩振幅降低比预报回归方程式(6)进行逐步回归分析，建立影响微型单排隔振桩隔振效果的敏感因素权重分析模型，如表6所示。

表6 微型单排隔振桩隔振效果的敏感因素权重分析模型

注：a模型预测变量：隔振桩桩长α1；b模型预测变量：隔振桩桩长α1、α1α4；c模型预测变量：隔振桩桩长α1、α1α4、桩间距α2；d模型预测变量：隔振桩桩长α1、α1α4、α2α4、桩间距α2；e模型预测变量：隔振桩桩长α1、α1α4、α2α4、桩间距α2、α3α4；f模型预测变量：隔振桩桩长α1、α1α4、α2α4、桩间距α2、α3α4、振源距α3。

由表6可知：对于由微型单排隔振桩桩长和常量共同建立的模型a，R2=0.485，调整后R2=0.463。影响振幅降低比的因素按照权重大小排序依次为：隔振桩桩长α1>振源距α3>交互作用α1α4>桩间距α2>交互作用α2α4>交互作用α3α4>振源距α3，对应的影响权重为：0.485、0.141、0.113、0.086、0.085、0.026。

由因素权重分析结果可知：影响微型单排隔振桩隔振效果的主要单因素为微型隔振桩的桩长，对隔振效果提高的贡献度为48.5%；其次为桩间距，对隔振效果提高的贡献度为11.3%；交互作用对隔振效果的影响，体现在微型隔振桩的桩长与桩截面宽度，对隔振效果提高的贡献度为14.1%。

因而在实际工程中采用微型单排隔振桩进行隔振时，尽量采用桩长度较大的混凝土隔振桩；在考虑多敏感因素交互作用的影响时，主要综合考虑微型隔振桩的桩长与桩截面宽度，以获得较好的隔振效果。

5 结论

通过建立多因素交互作用下的微型单排隔振桩振幅降低比简化预报模型，在经过方差分析简化修正后，可作为在一定适用条件下的微型单排隔振桩振幅降低比预报模型，为微型隔振桩的选择及布置方式提供合理的依据。同时得出以下结论。

(1)影响微型单排桩振幅降低比的因素按照重要性大小排序依次为隔振桩桩长α1>振源距α3>交互作用α1α4>桩间距α2>交互作用α2α4>交互作用α3α4>振源距α3，对应的影响权重为：0.485、0.141、0.113、0.086、0.085、0.026。

(2)影响微型单排隔振桩隔振效果的因素主要是微型隔振桩的桩长以及相邻隔振桩的净距，对微型隔振桩隔振效果的贡献为62.6%。

(3)影响微型单排隔振桩隔振效果四因素的交互作用主要体现在隔振桩桩长和桩截面宽度之间，对隔振桩隔振效果的贡献为14.1%。

(4)在实际工程中采用微型单排隔振桩进行隔振时，采用桩长度较大的混凝土隔振桩；在考虑多敏感因素交互作用的影响时，综合考虑隔振桩桩长与桩截面宽度，以获得较好的隔振效果。