《表面涂色的正方体》教学设计

刘勇生

【教学内容】

浙教版五年级下册第114页。

【教学目标】

1.让学生经历把表面涂有颜色的正方体切成若干个同样大的小正方体的过程，引导学生探索发现表面涂有颜色的小正方体的各种情况以及其中隐含的简单规律。

2.使学生进一步积累探索简单数学规律的经验，感悟数学思想方法，发展数学思维能力和空间观念。

3.使学生在探索数学规律的过程中，感受数学的结构美，获得发现数学规律的愉悦体验，激发学生学习数学的兴趣。

【教学重、难点】

1.探索并发现几何体表面涂色情况的变化规律。

2.应用发现的规律解决一些简单的实际问题。

【教具准备】

PPT课件、教师自制学具。

【教学过程】

一、谈话导入，激发兴趣

师：（出示正方体）上节课我们认识了正方体，谁能说说正方体有什么特征？

生：正方体有6个面、8个顶点、12条棱。

师：如果给正方体6个面涂上色，再把每条棱平均分成3份，切成一个个小正方体，你能想到哪些数学问题？

生：一共有几个小正方体？

生：三面涂色的小正方体有几个？两面涂色的小正方体有几个？一面涂色的小正方体有几个？没有涂色的小正方体有几个？

师：这些小正方体的表面涂色情况不一样，有些是三面涂色、有些是两面涂色、有些是一面涂色，有些是没有涂色，你能分别指出一个吗？

（学生上台指，教师PPT展示）

师：今天我们就一起来研究《表面涂色的正方体》。（板书）

【设计意图：学生在学习本课前已经认识了正方体，所以这里设计了两个教学环节，一是让学生通过想象同时教师课件展示提出数学问题；二是给学生展示正方体的各种涂色情况，方便学生后续研究。】

二、经历过程，探究规律

研究内容：把棱长平均分成3、4、5份后，三面、两面、一面、没有涂色的小正方体各有多少个？

合作要求：

1.选择适合自己的学习材料独立探究。

A.学习单上的正方体图。

B.正方体学具。

2.独立完成学习单。

3.完成学习单后，在小组里交流你的方法。

师：我们合作学习时，要注意什么？

生：独立研究，静静思考。

师：请同学们静静地独立探究，完成探究后轻声地交流方法。

【设计意图：通过独立思考探究，让每位学生都能动手动脑，都能得到初步的活动经验，能充分地理解后续的研究。通过小组内交流，让学生把自己的思考过程组织成语言为汇报做准备，让思路不是特别清楚的学生能够思路清晰。】

（学生探究，教师巡视）

汇报 1：学生汇报 3×3×3。

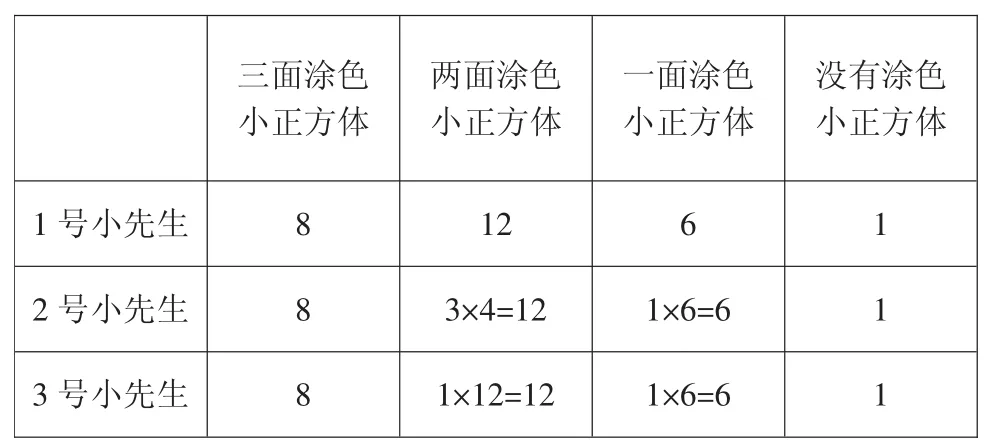
师：大家能看明白吗？看懂的同学来说一说。

师：1号、2号小先生看懂3号小先生的方法了吗？看懂的说一说。

师：棱长三等分的还有补充吗？

师：刚才我们研究涂色小正方体的数量，谁来说一说它们分别在什么位置？

生：三面涂色的小正方体在大正方体的顶点（板书：顶点），两面涂色的小正方体在棱上。

师：两面涂色的小正方体在棱上吗？

生：棱中间（板书：棱中），一面涂色的小正方体在面中（板书：面中），没有涂色的小正方体在体中（板书：体中）。

【设计意图：教师在学生探究过程中，选择不同层次的学生作为1、2、3号小先生，再让他们分别汇报，最后追问1、2号是否明白3号的想法，并说一说3号方法，让和1、2号一样的方法的学生去感悟3号方法的优点。】

汇报 2：学生汇报 4×4×4。

师：把棱长分成四份，谁来说说每种涂色的小正方体各有多少个？你是怎么想的？

生：三面涂色的小正方体有8个，两面涂色的小正方体有2×12=24（个），一面涂色的小正方体4×6=24（个），没有涂色的小正方体有8个。

师：你们明白他的想法吗？谁来说一说？

师：还有其他的方法吗？

生：三面涂色的小正方体有8个，两面涂色的小正方体有（4-2）×12=24（个），一面涂色的小正方体（4-2）2×6=24 个，没有涂色的小正方体有（4-2）3=8（个）。

师：谁听懂他的想法了？有什么问题？

师：我们把棱长四等分，为什么两面涂色的小正方体每条棱上只有两个呢？

生：每条棱有4个小正方体，要减去顶点2个三面涂色的小正方体，所以是4-2。（PPT展示）

师：每条棱是四等分，每个面上一面涂色的小正方体个数为什么是（4-2）2呢？

生：棱长4等分，每排4个减去左右2条棱，有4 排减去上下 2 条棱，所以（4-2）×（4-2）=（4-2）2。

师：你能想到没有涂色的小正方体是怎么排列的吗？

生：是比原正方体小一号的正方体，把它的表面剥掉一层。（PPT展示）

师：为什么没有涂色的小正方体每条棱都是2呢？

生：上下左右前后各少一层，所以是（4-2）×（4-2）×（4-2）。

【设计意图：本环节汇报是在3×3×3的基础上进行研究的，研究棱的等份数和个数的关系，所以本环节汇报时借助PPT学生更容易理解，并且反复追问棱的等份数和个数之间的关系，让学生能够感悟表面涂色的正方体的基本规律】

汇报 3：学生汇报 5×5×5。

师：谁来汇报棱长五等分的情况？

生：三面涂色的小正方体有8个，两面涂色的小正方体有3×12=36（个），一面涂色的小正方体有9×6=54（个），没有涂色的小正方体有 3×3×3=27（个）。

师：谁能用棱长五等分来表示？

生：三面涂色的小正方体有8个，两面涂色的小正方体有（5-2）×12=36（个），一面涂色的小正方体有（5-2）2×6=54（个），没有涂色的小正方体有（5-2）3=27（个）。

师：我们研究了棱长三、四、五等分的，还需要研究六、七、八等分的吗？为什么？

【设计意图：本环节在 3×3×3、4×4×4 的基础上进行汇报，选前面汇报有困难或者没有举手的学生汇报，让学生获得学习成功的满足感。】

三、观察比较、归纳规律

师：静静地想一想你发现了什么规律？写在学习单上。（教师巡视分层次）

师：谁上来汇报？（学生分层次汇报）

第一层次：不管把大正方体的棱平均分成几份，三面涂色的小正方体都在顶点，都有8个；两面涂色的小正方体都在棱中间；一面涂色的小正方体都在面中间。

第二层次：能找出一条棱上有几个小正方体两面涂色的方法；能找出一个面上有几个小正方体一面涂色的方法。

第三层次：用字母总结出规律。（板书）

三面涂色小正方体：8

两面涂色小正方体：（x-2）×12

一面涂色小正方体：（x-2）2×6

没有涂色小正方体：（x-2）3

四、回顾过程，反思得失

师：今天这节课你有什么收获？

生：找每种涂色的小正方体时，要注意它们在大正方体上的位置；找小正方体时把找、数、算等方法结合起来，根据图形的特征进行思考。

【设计意图：本节课的设计理念基于开放的课堂，通过学生提出问题和独立探究活动获得基本的活动经验，在小组交流和分层次汇报中让学生获得基本的方法，通过再次汇报获得棱的等份数和涂色面个数之间的关系，最后通过学生的汇报交流得出规律，在整个教学的过程中教师主要的作用就是引导，而学生是整个过程的主体。】