基于信号趋势的自适应分解方法研究

华北理工大学 王 猛

信号的分解质量直接影响着信号的时频分析，目前已有的信号分解方法都是按照信号频率由高到低进行分解。本文提出一种基于信号趋势的自适应分层和提取方法，按照信号频率由低到高，逐层实现信号的分解，通过仿真实验验证了该方法的可行性。这种处理方法为自适应分解方法提供了新的思路，对分解出的趋势分量采用希尔伯特变换进行相应的时频分析，求得瞬时频率等参数，绘制信号的时频谱图，并对分解过程中的端点效应进行了分析，完善了分解过程。

1.前言

信号是信息的载体，现实物理世界中，我们所接触到的信号的频率和幅度每时每刻都在发生变化。通常情况下，在同一时刻,信号包含了多个频率分量，这样的信号被称为多分量信号,如光谱信号、生物电信号、雷达信号等[1]。在对这样的信号进行分析处理时，频率参数精准方法的确定就显得格外重要。

傅里叶变换（FourierTransform）是最早提出的信号变换域处理方法，它能够反映信号在频域中的特点。通过傅里叶变换，我们可以获知信号的频域信息[2,3]。然而，绝大部分信号的频率都是随时间变换的。傅里叶变换是一个全局变换，它反映信号在整个时间区间内的频域特征，并不具备信号局部分析能力，不能得到信号的时变信息。因此，傅里叶变换只适合于时不变信号。

时频分析方法，可以直观展示信号的瞬时幅度和瞬时频率[4,5]。时频分析法将时域中信号的表现形式转变到时-频平面上，可以对信号的时变特征进行分析。在时频分析中，采用瞬时频率与傅里叶频率相对应，瞬时频率是信号频率在时间上的瞬时体现，是信号在该时刻下所具有的频率值。

当每一时刻的频率值具有唯一单值时，信号被称为单分量信号[6,7]。相比多分量信号，单分量信号不存在信号频率的混合项，单分量信号的瞬时频率才有确定的意义。因此，在进行信号的时频分析时，基本方法是对待分析信号进行分解，再对分解出来的子信号进行分析。

如小波变换（Wavelet Transform），小波变换是分析和处理非平稳信号最成功的工具。Mallat所引入的小波多分辨率分析[8,9]可以按需要实现信号的子带分解。目前，小波变换已在各个领域取得了广泛的应用，但是，小波变换也有不足：小波分解同样属于一种局部的信号分解方法，通过设定窗口的不断平移，达到分解的目的。在对信号实施小波变换前，小波变换的基函数需要预先指定。而基函数一旦指定，在对该信号分析的过程中间，基函数保持不变。也就是说，基函数的选择缺乏自适应性。目前绝大部分信号分解的方法都不是自适应的，其基本方法都是选择一个基函数将信号分解为一系列的简单分量。

1998年，Hilbert-Huang变换的提出[10]为非线性信号的分析与处理开辟了一条新颖的途径，Huang采用了经验模式分解（Empirical Mode Decomposition）将一个复杂的信号分解为一系列简单信号，先得到固有模态函数（IMF）[11]，然后对IMF分量进行希尔伯特变换，求得瞬时频率和瞬时幅值，这个分解过程也不像小波变换或其他变换那样预先选定基函数，而是取决于信号本身，因而它是自适应的，且是高效的[12,13]。但是经验模态分解过程中IMF分量之间的正交性是通过筛分迭代算法近似实现的，还没有得到彻底的解决方案和完整的理论解释，从而不可避免的导致能量的混叠和频率的交叠。

同时现有的基于HHT思想的信号分解方法都是按照频率从高到低[14,15]，依次将高频信号分量分解出来。这种分解方式虽然适用性广，理论成熟，但是在分解过程中，由于高频分量的存在，容易对低频分量造成影响，误差大或分解不完全。故本文提出一种基于信号趋势的自适应分解的方法，对信号的趋势进行了数学描述，按照频率由低到高，依次实现信号的分解，具有很强的实用性，同时对分解过程中产生的端点效应采用周期延拓的方法进行了有效的抑制，完善了整个分解过程。

2.基于信号趋势的自适应分解方法

2.1 信号的趋势线函数

定义1：对于任意给定信号，由信号的全部极值点构成的上、下包络线，可得中心线A(t)，信号在时间域上变化的中心轴线即为趋势线函数f(t)。即：

一般来说，信号的趋势线函数是一个相对的概念，一个信号的趋势线函数往往不是一个简单函数。

定义2：对于任意给定的信号f (t)，若其趋势线函数A(t)在每个时刻的值都为零，则称A(t)为零趋势函数。实际应用中，考虑运算误差，可设定任意小的一个正数，使每一时刻的，即：

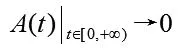
则A(t)可视为零趋势函数。例如常见的调幅信号与调频信号，皆为零趋势信号。

2.2 分解过程

基于信号趋势的自适应分解方法，通过不断获取当前信号的极大值与极小值，进行样条插值，将信号恢复至原始长度，并求其中心线，以获得趋势线函数，达到信号的逐层分解，当分解出零趋势线时，分解终止。对于任意给定长度为N的非零趋势信号x(t)，其分解具体过程如下：

（1）分别求得信号x(t)所有的全局极大值点与极小值点，数量分别为N1与N2。

（2）采用三次样条插值，对N1个极大值点与N2个极小值点进行插值，获得长度为N的极大值包络xmax(t)与极小值包络xmin(t)。

（3）求极大值与极小值包络的均值得到第一层信号分量，记为m(t)：

检查m(t)是否为零趋势函数，若满足，即为第一个分量，若不满足，继续下述过程。

（4）取

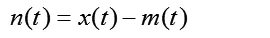
重复（1）（2）（3），检查n(t)是否满足是零趋势线，若满足，即为第一个分量，若不满足，使：

将n(t)当作原始信号，重复步骤（1）（2）（3）（4）。至ni(t)是零趋势线时，分解出第一个趋势线函数。

（5）记

其中N为循环次数，则c1(t)为信号x(t)的第一个被分解出来的趋势线分量，并且在x(t)所包含的分量中频率最低。

（6）取信号

重复步骤（1）（2）（3）（4）（5），依次得到频率由低到高的趋势线分量c2(t)、c3(t)，…，ck(t)。

（7）当

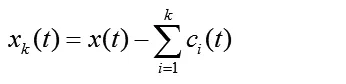
为零趋势线时，分解终止。此时：

为最高频信号。

3.仿真结果与讨论

3.1 基于信号趋势的自适应分解

仿真实验一采用由三种不同频率的正弦信号叠加成的混合信号作为输入信号，时间区间设置为[0,1]，信号长度N=4001，令sig=20sin(20πt)+10sin(200πt)+5sin(2*103πt)，其时域图如图1所示：

夹纻胎轻巧、牢固，成型后不易变形、开裂，留存时间长。从工艺角度看，造型的自由度增加了，能够制造更为丰富多样的器型。夹纻器的出现是漆工艺的一次革命，也为漆器生产的兴旺发达奠定了基础。夹纻器最早出现在战国时期，两汉中期以后盛行起来，成为最常见的制胎方法。魏晋南北朝以来，常采用夹纻胎工艺制作佛像。塑造的佛像十分轻便，可以车载、人抬游行于街市，达到宗教宣传的目的。遗憾的是，唐末武宗灭佛，大量夹纻造像遭到毁坏，也导致这项工艺的失传。到了清代，福州沈绍安恢复了传统的“纻胎”工艺，并在此基础上创造出著名的“脱胎漆器”。

图1 实验一输入信号

采用基于信号趋势的自适应分解方法，对输入信号进行分解，得到的各趋势线分量如图2所示：

图2 实验一趋势分量

采用希尔伯特变换，求解趋势线分量的瞬时频率和振幅，绘制时频谱图，如图3所示：

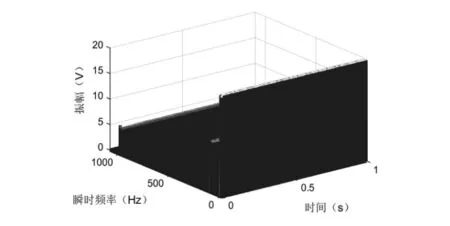
图3 实验一时频谱图

通过时-频谱图，可以看出，仿真实验一中分解出的趋势线分量时频平面特征体现明显，能够清楚的获知原信号分量数与频率特征。

仿真二采用线性趋势信号，时间区间设置为[0,1]，信号长度N=4001，一次函数y=8000t+1000,正弦信号x=500*(200πt)，输入信号sig=x+y,其时域图如图4所示：

图4 实验二输入信号

采用基于信号趋势的自适应分解方法， 对输入信号进行分解，得到的各趋势线分量如图5所示：

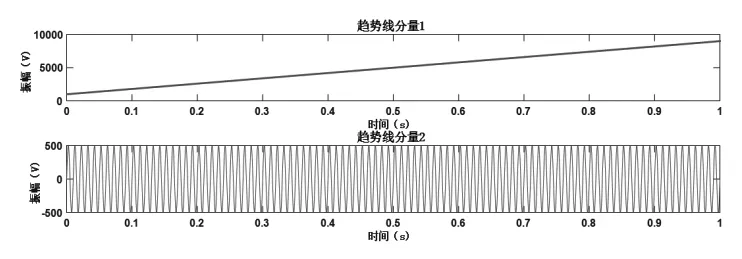
图5 实验二趋势分量

采用希尔伯特变换，求解趋势线分量的瞬时频率和振幅，绘制时频谱图，如图6所示：

图6 实验二时频谱图

通过时-频谱图，不难看出，仿真实验二中分解出的趋势线分量时频平面特征体现明显，在任意t点处都有唯一的瞬时频率值与其对应，其瞬时频率具有单一性。但是在趋势线信号端点处瞬时频率值发生了发散，出现了端点效应。

3.2 分解过程中端点效应的抑制

延拓的信号如图7所示：

图7 延拓后的信号

分解后的趋势线分量如图8所示：

图8 延拓后的趋势分量

依据希尔伯特变换，求取整个时间区间内的瞬时频率和振幅，截取[0,1]信号趋势线分量，绘制时频谱图，如图9所示：

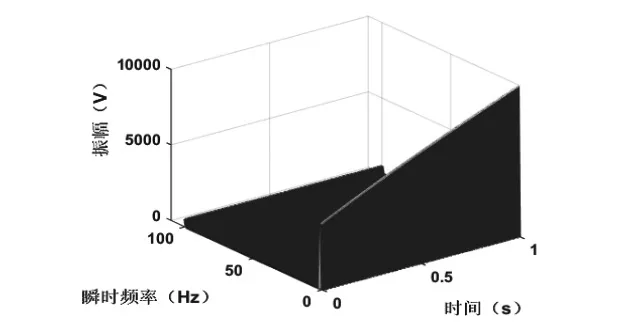
图9 抑制端点效应后的时频谱图

通过信号的时频谱图可以看出，相对于仿真三中出现的端点处信号瞬时频率值发散的情况，采用周期延拓的方法，可以有效地抑制。

4.分析与总结

通过仿真实验可以看出，基于信号趋势的自适应分解的方法能对信号进行自适应的分解，通过分解出的趋势分量求解瞬时频率和振幅，绘制时频谱图，能够很好地体现信号的参数特征。针对分解过程中出现的端点效应，采用信号周期延拓的方法，可以很好地抑制。

现有信号分解或信号变换的基本思路是大多数将信号和一组函数作内积，从而得到一组标量，即信号离散表示的系数。由于正交基具有很多优点，因此，在信号处理中正交基的应用最为广泛。如小波变换。但是由于针对不同信号，基的选择明显不同，故自适应程度较低，分解成本较高。该方法为一种数学方法，相对于选择不同的基，自适应程度高。相对于使用广泛的经验模态分解与局部均值分解，其过程是按照信号频率由高到低，逐层进行分解，降低了高频信号对低频信号分量的影响，较好的保留的信号的固有趋势，可行性与可操作性极高。