基于小波神经网络的电力系统故障检测方法

安徽理工大学电气与信息工程学院 张小乐

1 引言

小波变换是近十年来一种强大的数学工具，小波变换在电力系统信号处理中得到了广泛的应用和研究。主要应用在故障信号分析，去噪，检测和谐波检测以及传输线故障定位等方面。但是，小波变换的应用一般局限于小范围，主要原因在于小波构造和存储的大规模应用需要花费非常多的时间。神经网络是处理大量数据的有力工具，在模式识别，函数逼近和非平稳随机信号方面神经网络具有独特的优势和逐步的详细描述以及特征提取能力，这些工具的组合就是小波神经网络。

小波神经网络以及相应的数学工具和相关传输线设备的优势，可以准确定位和诊断故障，这是电力系统故障诊断技术的发展趋势。它不仅可以减少和防止故障对电力系统的影响，使系统尽快恢复正常运行，减少经济损失，更重要的是，对提高电源的安全性和可靠性也有很大帮助。

2 小波神经网络

2.1 小波变换理论

设基小波ψ ( t )∈L2( R )满足容许条件：

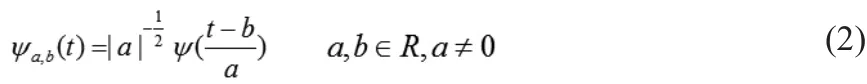
ψa,b( t )称为小波函数（wavelet function），其中a,b分别为尺度伸缩（scale dilation）参数和时间平移（time translation）参数。信号f ( t )∈L2( R )的连续小波变换定义为：

2.2 小波神经网络的理论基础

小波神经网络理论基于重构小波函数：满足基小波的可容许条件，扩张和平移，形成密集L2(R)中小波的连续线性组合。如果ψ ( t )∈L2( R )满足：

所以ψ(x)称为基小波函数，ψ(ω)由ψ(x)傅立叶变换而得。通过(1)式我们可以得到：

函数ψ(x)是收敛的，在时域和频域都是局部非零紧支撑函数，它通过伸缩和平移得到，是一个小波族：

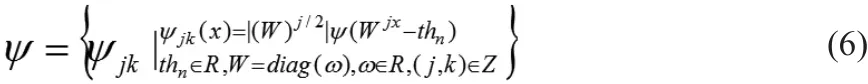
定理：对于任何f ( x ) = L2( R )小波函数的框架族满足条件ψ：

定理表明，任何 f (x)都可以使用任意精度的小波逼近。

2.3 小波神经网络结构

小波神经网络结构如图1所示，通过研究样本，其中压缩输入层投影作用于小波神经网络在图1中，有M个输入节点，隐藏层有K个节点，输出层有N个节点，对于给定的一组输入和输出样本P，Xm（m=1，...M）用于网络输入，Yn（n=1，...N）表示网络输出。选择隐藏层作为Morlet小波小波，网络的输出也不是简单的加权和，而是网络隐藏层上的第一个节点输出的小波加权和，Sigmoid函数变换，得到了最终的网络输出。这有助于处理分类问题，同时减少训练期间分歧的可能性。

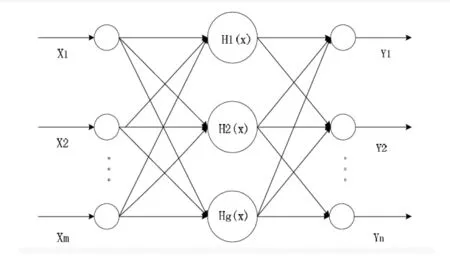
图1 小波神经网络结构

3 小波神经网络在电力系统故障检测中的应用

3.1 小波神经网络的构造

小波在时域和频域具有良好的定位性能，当神经网络和小波变换时，神经网络功能可以进一步改善。普通神经元模型是一组具有S形激活函数的输入组合，其线性神经元神经元，S形小波神经网络激活功能转化为小波函数，其神经元可被认为是非线性神经元。目前很多小波函数，有些已经使用了神经网络。该小波函数构造成应用于故障检测。

其中：f (x)表示S形函数；A和B为扩展比例因子；ψ(x)是指数衰减的奇函数，因此，满足小波容许条件，它构成一个小波网络。

3.2 仿真模型

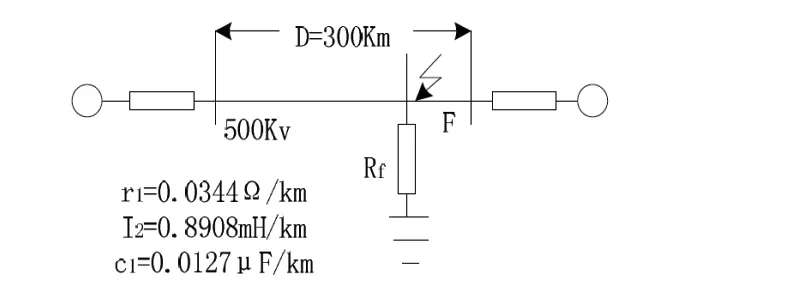
图2 电力系统仿真模型

3.3 仿真结果

在这里对同一故障进行过渡电阻训练误差的研究是0.1，在200km传输线故障类型10和非故障状态结束时首先保留线路样本。可变故障Rg电阻为0Ω，20Ω，50Ω，150Ω和200。对于两相短路接地故障，相变电阻Rf为0.2Ω，5Ω和20Ω，考虑到训练收敛系统，数据复制次数的需要，将无故障样本数据复制9次，得到的研究样本为100。小波网络训练的收敛时样本数约为4.0×105。

表1显示了单相测试结果Q1～Q4分别表示A相，B相，C相和地。如果A相有故障，那么Q1的预期值为1.0；另一方面0.0的预期值。Q2～Q4与之同理。

表1 单相故障测试结果

4 结论

各种智能技术将结合混合智能故障诊断系统是一种发展趋势的诊断。小波神经网络作为一种组合神经网络和小波分析工具，不仅具有非平稳信号的小波分解能力，而且完全继承了神经网络的优点：自学习，自适应，高容错等特点，理论分析和仿真试验表明，基于小波神经网络的故障识别，与传统的分析方法相比，其响应速度和精度都有明显提高，为采取适当的保护方法提供了前提条件。它在电力系统故障诊断中得到人们的关注程度也会也来越高。

引文

①Ren Zhen.Wavelet analysis and its application in power system.Bei Jing:China Electric Power Press,2003,11.

②HO DWC Zhang Pingan Fuzzy wavelet new works for function leaning[J].IEEE Trans on Fuzzy Systems,2001,9(1):200-211.

③Zhang Qinghua Using wavelet networks in non para metric estimation[J].IEEE Trans on Neural Networks,1997,8(2):227-236.

④Sujit Kumar Sahoo,Anamitra Makur.Dictionary Training for Sparse Representation as Generalization of K-Means Clustering[J].IEEE Signal Processing Letters,2013,20(6):587-590.

⑤Chi-JuiWu,Tsu-HsunFu,Chaung-Wei Wu.Discrete wavelet transform applied to data Compression of wave forms with harmonic and voltage flicker[C].Power Engineering Society Winter Meeting,2002,1141-1146.

⑥周静,陈允平,周策,梁劲.小波系数软硬阈值折中方法在故障定位消噪中的应用[J].电力系统自动化,2005(01).

⑦葛哲学.小波分析理论与MATLAB R2007实现[M].电子工业出版社,2007.

⑧刘海青,柳劲松.Fourier分析和小波分析在信号时频分析中的特性比较[J].平原大学学报,2000,17(3):71-74.