海底隧道火灾车辆疏散优化模型研究

陈明仙，许贵贤

(福建船政交通职业学院安全技术与环境工程系, 福建 福州 350007)

公路海底隧道兼具地下工程、海底工程属性，一旦发生火灾事故，容易造成严重后果.火灾事故发生后，如何在第一时间内将隧道内的车辆清空至安全出口，同时满足疏散路径上的流量限制要求，避免人员受高浓度CO的长时间伤害，合理制定车辆疏散方案，进行时空路径的合理分配，以实现最安全、最有效的车辆疏散是一个亟需解决的问题.

针对海底隧道车辆疏散这一问题，国内外学者进行了一些研究.如Henning等[1]对挪威海底隧道事故和火灾进行分析，对于发生事故的机率和流量分布进行了分析；Emmanuel等[2]建立了英吉利海底隧道应急的拥挤运动模型，运用疏散模型进行原始、真实疏散实际结果的测试比较，对集会模型和班车疏散实验的结果进行比较分析，为集会模型仿真软件提供了支持.边少君等[3]建立了海底隧道三维仿真监控系统，实现了三维视角中应急设备、信息的展示，提供可视化的事故应急预案.

当前关于海底隧道车辆疏散相关应用研究多集中于事故影响参数分析、指令分析、应急模拟和个体运动模型等方面，而对于车辆动态交通流疏散模型方面研究较少.因此，笔者将以厦门翔安海底隧道为例，考虑海底隧道路网结构特性、火灾应急特性和CO对人体伤害等多因素，建立动态交通流车辆疏散模型，并改进蚁群算法，设计模型求解算法，得出车辆疏散最优方案.

1 问题描述

海底隧道火灾发生后，进入应急情景，车行横洞开启，对向隧道入口实行管制，对向车道内车辆加速驶离，事故车道内车辆通过顺行车道、车行横洞和服务隧道等各通道进行疏散逃生.车辆在疏散过程中，各路段应急能力由于受流量限制与冲突会产生动态变化，静态疏散方案容易由于冲突导致拥堵影响疏散效率[4].同时，在传统疏散过程中，不考虑火灾过程CO对人体的伤害，可能导致应急过程中止，综合安全效益低下.此时，如何在第一时间内将隧道内的车辆清空至安全出口，同时满足疏散路径上的流量限制要求，避免受高浓度CO的长时间影响，合理制定车辆疏散方案，进行时空路径的合理分配，以实现最安全、最有效的车辆疏散是一个急待解决的问题.该问题为典型的多约束的应急疏散组合优化问题[5].

2 模型构建

为解决海底隧道火灾情景下车辆疏散问题，可通过动态的交通流分配优化，根据疏散演进变化而生成最优方案，保证模型目标实现，同时不致在实际疏散时产生拥塞，更具实用性.

应急疏散过程的动态交通流分配是根据疏散需求点和疏散目标点位置，在可用疏散交通路网环境下，按照确定的优化目标确定从疏散点至安全出口的最优化路径，车辆在该路径上按照一定规则行驶；在此基础上，考虑路网内各可用路径的承载能力，合理规划和分配各个路径上的交通流，提高路网的综合使用效率，保证疏散网络的可靠性，降低疏散过程的交通延误，保证疏散过程人员的伤害在限值内，并且使应急疏散综合效益达到最大化[6，7].

2.1 目标函数

在车辆疏散情景下，目标函数可描述为使海底隧道疏散过程的总成本最低，可表达为：

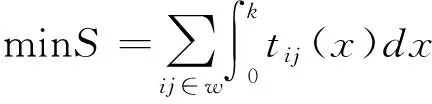
(1)

其中：W为车辆x的疏散路径集合；

k为海底隧道中所需疏散的车辆数；

tij(x)为车辆x在疏散路径(i,j)上的出行时间；

式(1)表达的意义为：应急疏散系统优化问题研究海底隧道区域内总数为k的被疏散车辆，对于x车辆有W个疏散方案，通过求解总数为k的被疏散车辆总累积时间成本最低使应急疏散系统整体效率最优.

在海底隧道动态疏散过程中，主要的疏散时间成本为交通阻抗，其组成为通过固定路径所需的时间与克服路径上流量及变化产生阻抗所需时间[7]，可表达为：

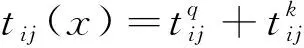
(2)

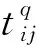
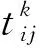
2.2.1 约束条件

(1)流量守恒约束

对于任一流量节点，节点流入流量值与流出流量值相等.而在任一节点上可能产生的新流量可为流入流量，即为流量守恒约束[7]，可表达为:

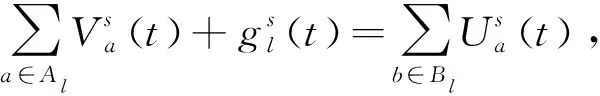
(3)

其中：Al表示能够到达l点的路径集合；

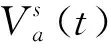
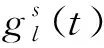
Bl表示从l点出发的可达路段集合；

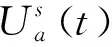
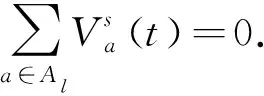
2.2.2 车流量限制

对于海底隧道可用疏散路网，左线、右线、服务隧道等各可供使用的疏散路段在应急状态下的通行能力存在差异.在应急疏散车流量分配时，需考虑各路段可承受的最大交通流，通常用单位时间内可承载的最大车辆数表示.此时，将路段上的车辆视为静止、连续分布，可承载最大流量即表达为给定时间内某一路段的最大车辆数.车辆在路径选择时，先对对象路段车流量超限情况进行判定，若未超限，则列为可进入路段；若超过上限，则将该路段列为不可选择路段[8].车流量限制可表达到：

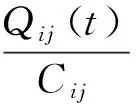
(4)

式中：Qij(t)为t时刻路径(i,j)上的车流量；

Cij为路径(i,j)可承载最大流量.

(5)

2.2.3 交通流分配规则

在疏散过程的动态交通流分配中，必须确定交通流中的车辆分配顺序.基于海底隧道应急情景特性，模型选择“先进先出”规则为基础交通流分配规则，对于确定路段，进入路段的车辆先后顺序与离开该路段的顺序一致.

2.2.4 CO伤害限制

车辆在路网中行进时，累计所受CO伤害值不能超过限制，否则疏散车辆内人员因身体伤害超限，会引起死亡或不可逆伤害，同时导致车辆疏散过程中止或受阻[9].

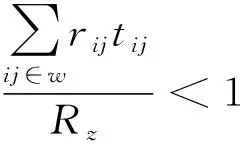
(6)

式中：rij为路径上人员单位时间CO摄入量；

Rz为累积伤害限值.

2.2.5 非负约束

Qij(t)≥0

(7)

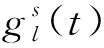
(8)

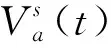
(9)

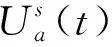
(10)

根据ACGIH化学物质阈限值，考虑CO对人体伤害机理、事故情景演变过程、应急通风特性和人员行为特性要素，计算累计伤害阈值Rz，则：

(11)

式中：

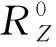
该系统主要采用JSP语言编写，开发环境为MyEclips,服务器采用Apache Tomcat，数据库采用MSSQL Server2005。

α1为运动系数，与人员运动强度和紧张情绪成反比，人员步行疏散时系数较低，取[0,1]；

α2为阈值飘移系数，特殊状态(如事故状态)下阈值漂移上限不超过3倍，即取[0,3]；

tr为阈值时间系数，总接触时间不超过30min，即取[0,30]；

3 模型算法设计

蚁群算法具有分布式计算、自组织、正反馈等优点，搜索能力强，收敛快，对解决路径规划和组合优化问题有很强的适应性，并能取得良好的效果.根据模型的特性，结合海底隧道应急疏散特点，基于蚁群算法进行改进，设计模型算法与步骤.主要改进如下：

3.1 禁忌规则

在TSP问题中，为加快搜索速度、快速收敛，要求蚂蚁遍历所有节点，且限制其搜索次数有且仅一次.但在海底隧道车辆疏散过程中，各节点间的连接由海底隧道的路网结构决定，网络节点并非大型复杂网络，若仍然使用禁忌表，蚂蚁容易进入无路可走的情景，造成寻优过程失败.为避免此种情况，设计新的禁忌规则，允许蚂蚁有限制地访问已经过的节点，为每个节点设置访问表，记录该蚂蚁对每个节点的访问次数.当寻优过程满足以下2个条件时可将该邻接节点作为该蚂蚁的允许访问节点：①当前节点访问邻接节点次数低于允许访问次数；②蚂蚁路径无回路[10].

3.2 启发式信息

在基本蚁群算法中，仅考虑了两个搜索点间路径长度为蚂蚁转移的期望，比较单一.结合海底隧道应急疏散的特点，改进启发式信息，在车辆疏散过程中，除了考虑各路径长度对于蚂蚁路径选择的影响外，还应考虑蚂蚁与出口距离、路径疏散流量、路径CO浓度等因素的影响[11-13].

3.2.1 蚂蚁与出口距离影响

在海底隧道车辆疏散过程中，存在着多个疏散出口.以翔安海底隧道为例，车辆可能疏散出口含左线、右线、服务隧道出入口共六个，疏散对象最终疏散出口具有不确定性，为使蚂蚁能够快速找到出口，除了基本蚁群算法中将路径行程时间为启发式信息外，将蚂蚁与各第n个出口的位置距离引入启发式信息，使蚂蚁的搜索更具方向性，加快收敛过程.

考虑车辆疏散过程中交通流动态属性，在启发式信息中引入流量路阻，适时更新路径流量，诱导蚂蚁向路径流量未超限且相对空闲路段，提高疏散路网的整体效率.

3.2.3 CO浓度

在车辆疏散过程中，以致伤度较高的CO为代表的火灾烟雾会对疏散人员造成伤害，伤害与吸入烟气浓度、吸入量等紧密相关.在车辆疏散过程中，应优先选择CO浓度较底的疏散路径，降低人员伤害[9].

路径(i,j)上的启发式信息定义为:

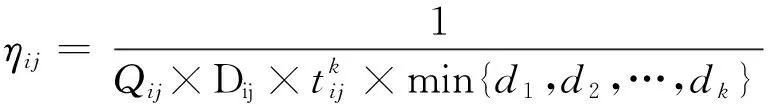
(12)

式中：k为疏散出口的个数；

Dij为车辆在疏散路径(i,j)上的危险值；

dk为车辆位置与出口k的距离

3.3 状态转移规则

为了提高算法的全局搜索能力，引入确定性选择和随机选择相结合的选择策略，并且在最优解的搜索过程中自适应地调整确定性选择的概率.这种选择方式称为伪随机比例状态转移规则，车辆k由节点i转移到节点j的规则如下[11]:

(13)

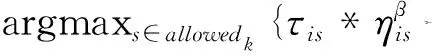
q为(0，1)区间内均匀分布的随机数；

q0为[0,1]之间的任一给定参数.

j的取值可以根据下面的公式(14)得出：

(14)

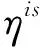
τis为路径(i,s)的的信息素量；

α为信息启发式因子；

β为期望启发式因子.

3.4 信息素局部更新规则

车辆k由节点i转移到节点j后，边(i,j)上的信息素量按式(15)、(16)进行更新[12，13]：

τij(t+n)=(1-ρ)·τij(t)+ρΔτij(t)

(15)

Δτ(i,j)=τ0或Δτ(i,j)=γ*maxa∈allowedkτ(i,s)

(16)

式中：allowedk为蚂蚁允许访问的节点集；

ρ为设定的信息素挥发系数；

Δτ(i,j)为路径(i,j)上的信息素增加量；

3.5 信息素全局更新规则

在每一波次疏散车辆均找到它们各自的最优路径和应急出口后，通过比较找出最短路径的轨迹，并仅对这条全局最优路径上的信息素进行更新[12]，具体更新规则见式(17)、(18).

τ(i,j)=(1-α)τ(i,j)+αΔτ(i,j)

(17)

Δτ(i,j)=

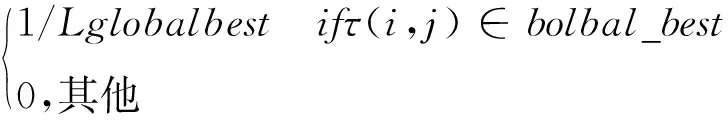
(18)

通过使用全局更新规则可更有效对搜索过程进行指导，使车辆路径的搜索集中在已有最优路径集合范围内，以提高搜索效率.

4 车辆疏散仿真算例分析

以翔安海底隧道客车自燃事故为例，假设自燃点位于隧道中部62号消防箱，进入火灾情景开始进行车辆疏散.

4.1 构建简化OD表

结合海底隧道的路网结构特征，根据模型研究的需要，将研究区域抽象映射并简化为疏散网络G=(V,E,f).其中V为节点集合，包括疏散起点、中间节点和目的地，E为各节点间的连接边，为疏散路径的抽象；f是V×V上的一个映射.单条疏散路径由疏散起点、中间节点、目的地和相应连接边组成.为方便车辆疏散模型运算与求解，构建简化OD表，并匹配CO探测器所探测CO浓度，如图1所示[14].

图1 路网OD

在车辆疏散阶段，由于人员处于非运动状态，只考虑紧张情绪影响，且为保证应急驾驶指令能够正确执行，取海底隧道应急状态下CO摄入量修正系数α1=0.6，α2=2，tr=20min=1200s，则Rz=25×0.6×1200×2=36000 cm3/m3·s=36000 ppm·s

疏散车辆速度常数为vv=3.5m/s；

4.2 模拟疏散

图2 原始状态车辆分布和疏散过程车辆分布

假设初期应疏散车辆分布如图2-1所示,隧道内车辆数为500，路径流量限制Cij=2000辆/小时,将车辆分为10波次进行疏散，每波次50辆.

根据海底隧道特点，结合前人研究经验[6-8]，取交通流批次为10，m=30，NCmax=100，α=1，β=1，ρ=0.9.运用编制的MATLAB程序，可得疏散过程车辆分布如图2-2所示.

疏散路径叠加如图3所示,图中不同颜色线路代表不同波次车队路径， 10波次车辆疏散路径分布如表所列.

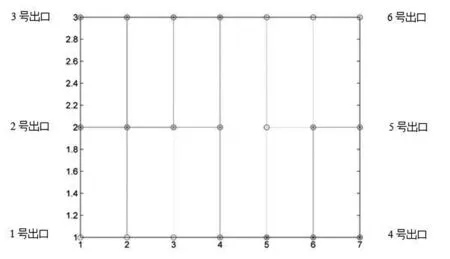
图3 疏散车辆路径分布

10波次车辆详细路径如表1所示.

表1 车辆疏散信息

4.3 结果分析

从模拟结果可以看出，通过动态交通流疏散，车辆在考虑路径和时间最短目标的同时，动态分配10批次的交通流，保证整体疏散效率，且避免了多车同时拥入同一通道导致拥堵，路网负荷分布合理，满足路网承载的约束条件；在路径选择上，合理充分利用6个应急出口，人工蚂蚁共避开CO超标路径2313次，所有路径CO摄入均在阈值内，避免了累积CO摄入值超限，有效避免人员伤害，并保证车辆疏散过程持续进行.