一类项链图在Klein瓶上的嵌入

刘新求

(湖南工程职业技术学院，湖南 长沙 410151)

1 研究背景

本文中关于曲面、嵌入、亏格等概念均与文献[1]一致.上世纪九十年代起，国内外一些图论学者开始研究图的亏格分布和完全亏格分布问题，并且做出了一些有价值的结论[2-7]，但是远远未解决这个问题，这是一个NP难问题.因为图在不同亏格曲面上的嵌入往往有相关关系.近十年来，有学者利用刘彦佩教授提出的联树模型和曲面运算理论[8]，转而研究一些图在某些小亏格曲面上的嵌入，譬如研究图在球面、射影平面、环面、Klein瓶上等曲面上的嵌入，也做出了一些颇有意义的结论[9-11].本文作者亦研究了两类广义项链图在射影平面上的嵌入[12].本文拟在此基础上，进一步研究其中一类广义项链图在Klein瓶上的嵌入.

2 引理和定义

为了表述方便，本文列出曲面运算理论的三种运算和三种关系.

运算1Aaa-⟺A

运算2AabBab⟺AcBc

运算3AB⟺(Aa)(a-B)

关系1AaBbCa-Db-E～ADCBEaba-b-

关系2AaBaC～AB-Caa

关系3Aaabcb-c-～Aaabbcc

定义2.1 若曲面S=…a…b…a…b, 则称边a和b在曲面S中交错，若曲面S=…a…a…b…b，则称边a和b在曲面S中平行(此处省略边的上标).

引理2.1[8]设曲面S1是可定向曲面且亏格为p，曲面S2是不可定向曲面且亏格为q，则有：

(1) 曲面S=S1xyx-y-可定向且亏格为p+ 1，曲面S=S1xx不可定向且亏格为2p+ 1；

(2)曲面S=S2xyx-y-不可定向且亏格为p+ 2，曲面S=S2xx不可定向且亏格为q+ 1.

定义2.2 设A是一个字母循环序，则由A中的某些字母按原来的相对顺序组成的字

母循环序叫做A的子列.

根据引理2.1，显然有以下结论：

引理2.2 在曲面S的多边形表示中，若其子列也能表示某个曲面S1，则S1

的亏格必定不大于S的亏格.

定义2.3 在两个节点之间连结m(m ≥ 2)条重边构成的图叫做双极图，记作Dm.

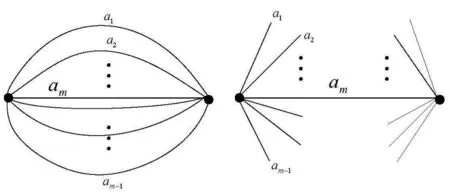
图1 图Dm及其联树

引理2.3[13]双极图Dm在球面上的嵌入个数g0(Dm)=(m-1)!.

引理2.4[14]双极图Dm在Klein瓶上的嵌入个数

定义2.4 在圈U2n=u1u2...u2nu1的节点u2i-1,u2i:i=1,2,3,…,n之间分别添

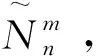
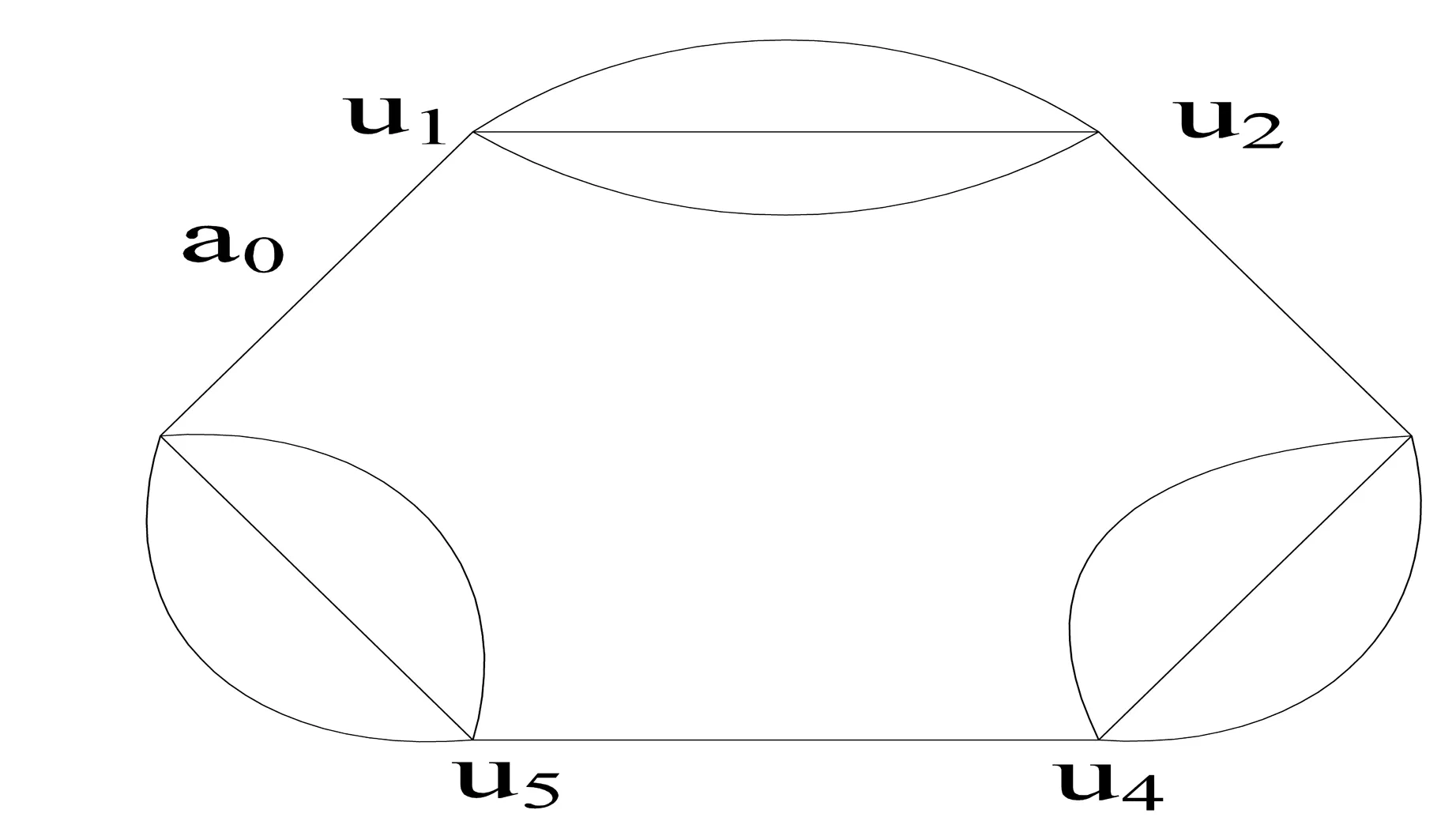
图2 项链图

3 主要结论

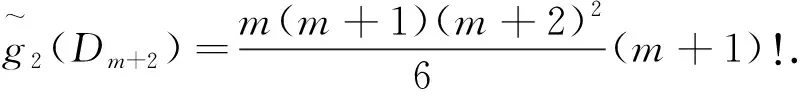
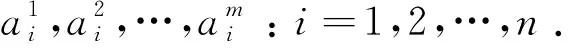
图3 图的联树

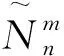
S=

嵌入情形1E1,E2,…,En中均不含有扭边.

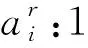
或者

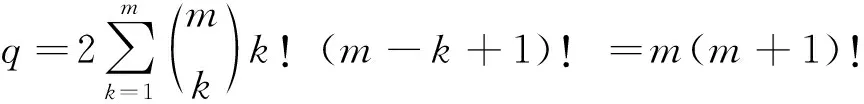
=[m(m+1)!+(m+1)!]n-(m+1)!n

=((m+1)n-1)(m+1)!n.

嵌入情形2E1,E2,…,En中恰有一个含有扭边.

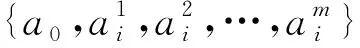
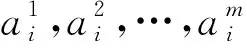
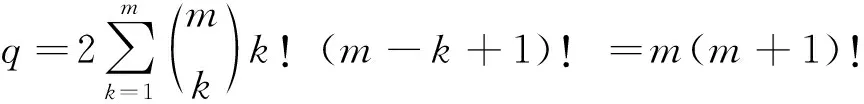
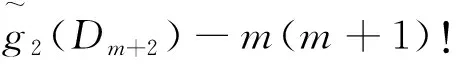
而对于i≠j，Ej中的边的放置方法均为(m+ 1)!种.令i=1,2,…,n,故嵌入情形2在Klein平面上的嵌入个数为

嵌入情形3E1,E2,…,En中恰有两个含有扭边.

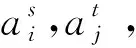
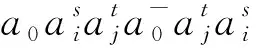
而

分别对应着2种不同的情形，所以以上子列实际上对应着16 种不同的情形.对于r≠i,j，Er中的边均为非扭边且其中每一条边所对应的两条半边均在生成树的同一侧，则有

从而Er的边的放置方法有(m+ 1)!种.

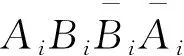
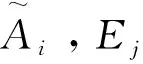
对其中每一种嵌入情形，Er(r≠i,j)的边的放置方法有(m+ 1)!种，Ei(Ej)的边的放置方法有

综上，嵌入情形3在Klein瓶上的嵌入个数为

把以上嵌入情形的嵌入个数相加即得定理结论.

令m= 1，立即得到以下推论：

推论3.1 项链图Nn,0在Klein瓶上的嵌入个数为(2n2+ 2n-1)2n.