平衡式双通带独立可控带通滤波器

张雨静，李蕴力，陈建新

(南通大学 电子信息学院，江苏 南通 226019)

0 引 言

现代无线通信技术和单片微波集成电路的高速发展促使通信系统对微波器件的抗干扰能力提出了更高要求。对比单端电路，平衡电路拓扑结构以其出色的抗共模干扰能力展现出了巨大的优势。随着越来越多的诸如功放、低噪放等有源差分器件的应用，为打造全面有效的全平衡射频前端系统，天线、滤波器等无源器件也被要求尽可能地采用差分结构。用平衡式滤波器取代传统的巴伦与滤波器级联，既实现了平衡电路的共模抑制特性，又符合当下设备小型化的趋势。在文献[1-3]中，采用了基片集成波导(substrate integrated waveguide, SIW) 来设计平衡滤波器，虽然它有很好的选择性，但基于此设计的滤波器尺寸相对较大。另外，还有许多被报道的平衡滤波器技术，例如，多模谐振器[4]，混合电磁耦合[5]和磁耦合共面波导[6]等。

双通带滤波器最早出现在上世纪90年代，最初是通过把2个独立的单通带滤波器连接起来构成，这种方法的缺点是电路尺寸大，而且插入损耗较大。由于微带电路有诸多优点，使得对微带双通带滤波器的研究在近几年有了较大的发展。特别是在小型化和高性能方面，基于基片集成波导的双通带滤波器[2]、基于阶跃阻抗谐振器(step impedance resonator, SIR) 的双通带滤波器[7]和基于枝节加载谐振器(stub-loaded resonator, SLR) 的双通带和三通带滤波器[8]等有了较大的发展。

本文设计了一个基于多模谐振器的平衡式双通带带通滤波器，通过在谐振器中心处加载枝节实现它的频率独立可控，通过控制金属化通孔的半径和2个谐振器之间的间距实现了2个通带耦合系数的独立控制，通过对馈线与谐振器之间的间距以及馈线与加载枝节之间间距的控制实现了2个通带外部品质因数的独立控制。其测试结果与仿真吻合良好。测试结果表明，该滤波器结构简单、尺寸小，并具有良好的差分通带响应和共模抑制能力。

1 谐振器理论

图1a为用于本文滤波器设计的多模谐振器结构，因其为上下、左右对称结构(图1a中虚线为对称面)，因而可用奇偶模分析法来研究其特性，它表示的是单个谐振器的等效电路图。图1a中的对称面可以模拟为奇模激励下的电壁，其等效电路如图1b所示。在偶模激励下，对称面表现为磁壁。偶模等效电路如图1c所示。从图1b和图1c可以观察到，这2个电路仍然对称，然后可以再次应用奇偶模分析来说明它们的谐振特性。这样就可由图1b得到图1d和图1e所示的等效电路图，由图1c得到图1f和图1g所示的等效电路图。图1d是图1b的奇模等效电路，图1e是图1b 的偶模等效电路，且偶模等效电路中比奇模等效电路多出的枝节即A段不影响奇模控制的频率(这里是通过奇模实现高频通带，偶模实现低频通带)。从图2中可以看出，高频和低频的频率都随B段长度的增加而下降，而低频的频率随枝节A长度的增大而减小，高频基本不随枝节A长度的变化而变化。因此，可以知道通过控制B段的长度来确定高频的频率，然后通过A段调整低频频率，从而实现频率的独立可控，图2验证了上述分析。

图1 枝节加载环形谐振器结构及其等效电路Fig.1 Structure of proposed stub-loaded ring resonator and its equivalent

图2 高频和低频的频率与图1e中A段和B段长度的关系图Fig.2 Lower and higher resonant frequencies versus the lengths of sections A and B in Fig.1e

另外，图1d和图1e还可以是相当于两端短路的半波长谐振器，如果在滤波器的中点处即它的接地端加电阻，那么这个电阻也是短路的，即相当于接地，不会破坏它的场。而图1f和图1g则是相当于四分之一波长谐振器，它是一端短路，一端开路的。如果在它开路的一端也就是电压最大处加电阻，就会破坏它的场，使它激励不起来，从而实现共模抑制。

2 平衡式滤波器设计

随着小型化滤波器的不断发展和进步， 越来越多结构复杂的滤波器被设计，然而其中大多数滤波器往往都不是独立可控的，免不了受其他因素影响。本文中设计的平衡式滤波器具有结构简单、双通带独立控制和良好的差分通带响应等优点，在实际生产和应用中具有很大的优势，其结构如图3所示。

由图3的俯视图可知，本文所设计的滤波器由3层结构，顶层和底层都是金属层，材料为铜，中间层为介质层，厚度0.813 mm，使用的材料是Roger RO4003(介电常数ɛr为3.55，损耗角正切为0.002 7)。

图3 平衡式双通带独立可控带通滤波器的结构示意图Fig.3 Structure of the proposed balanced bandpass filter with independently controllable dual passbands

2.1 耦合系数

本文设计的滤波器是通过拟合谐振器之间的耦合以及馈线和谐振器之间的耦合实现[9]。从图3的俯视图中可以看到有2个耦合区域，耦合区域Ⅰ是2个谐振器之间的缝隙耦合，它对低频和高频通带的耦合系数都有影响，且耦合系数主要受耦合区域Ⅰ微带线的长度和缝隙间的宽度控制；耦合区域Ⅱ 是金属化通孔耦合[10]，它主要影响低频通带的耦合系数，且耦合系数主要受微带线宽度和金属化通孔的半径控制。

基于耦合谐振理论，耦合强度可由耦合系数表征。耦合系数的提取可由(1)式得出

(1)

(1)式中：K12是耦合系数；f1和f2指的是在馈线和谐振器之间为弱耦合时，通带中S21的2个尖峰的频率。图4就是根据(1)式提取参数计算形成的。

图4 2个通带的耦合系数K12与金属化通孔半径r以及2个谐振器之间的间距a的关系Fig.4 Relationship between the coupling of two passbands K12 and the radius of the metallized hole r and the distance between two resonators a

从图4中可以看出，高频通带的耦合系数K12h随着谐振器之间的间距a的增大而下降 ，但低频通带的耦合系数K12l随谐振器之间的间距a变化较小；低频通带的耦合系数K12l随着金属化通孔的半径r的增大而减小，但高频通带的耦合系数K12h却不随金属化通孔的半径r的变化而变化。所以，由图4可知，2个谐振器之间的间距a主要是影响高频通带的耦合，而金属化通孔的半径r主要影响低频通带的耦合。因此，可以确定本文设计的这个结构2个通带的耦合系数是独立可控的。

2.2 外部品质因数

馈线和谐振器之间的耦合可以通过外部品质因数Qe来表示。为了提取外部品质因数，在提取时只保留了一对差分端口和一个谐振器。提取外部品质因数Qe的公式为

(2)

(2)式中：f0表示中心频率；f±90°表示与f0上下相差90°处的频率。依据(2)式提取参数计算并画出了图5。

从图5中可以看出，低频通带的Qel随着馈线与加载枝节之间的间距c增大而增大，而高频通带的Qeh基本不随馈线与加载枝节之间的间距c变化；低频通带的Qel随着馈线与谐振器之间的间距b增大而增大，而高频通带的Qeh随着馈线与谐振器之间的间距b的变化较小；由图5可知，馈线与加载枝节之间的间距c主要影响低频的Qel，而馈线与谐振器之间的间距b主要影响高频的Qeh。因此，可以确定该滤波器2个通带的外部品质因数Qe是独立可控的。

图5 外部品质因数Qe与馈线与谐振器的间距b及馈线与加载枝节的间距c的关系Fig.5 Relationship between the external quality and the distance named b between the resonator and the feeding structure, and the distance named c between the step and the feeding structure

3 仿真与实验

为了验证上述分析，本文设计的滤波器2个差分通带中心频率分别为f1=1.6 GHz和f2=2.5 GHz，低频通带的3 dB相对带宽为4.4%(对应0.09 dB的纹波带宽为2.96%)；高频通带的3 dB相对带宽为5.5%(对应0.06 dB的纹波带宽为2.64%)。

该滤波器的设计可以总结为以下几个步骤：①通过2个通带的中心频率可以确定图1d和图1e中A，B的长度；②根据纹波及其相对带宽(fractional bandwidth,FBW)，可以算出低通原型滤波器中低频的g0=1,g1=0.817 7，g2=0.612 8，g3=1.334 3，高频的g0=1，g1=0.728 5，g2=0.575 7，g3=1.265 4，进而算出滤波器的耦合系数K12和外部品质因数Qe,其公式为

(3)

(4)

根据(3)—(4)式计算所得，低频的K12l为0.041 8，Qel为27.625，高频的K12h为0.040 8，Qeh为27.594 7，再联合图4，图5中的参数拟合和优化，滤波器的物理尺寸最终确定为W1=1.2 mm，r=0.32 mm，a=0.16 mm，b=0.13 mm，c=0.3 mm，L1=19.32 mm，L2=54.56 mm，L3=11.1 mm，L4=10.43 mm。仿真和测试结果分别由Ansoft HFSS和Agilent N5230A PNA-L网络分析仪得出。图6是电路实物图；图7是滤波器仿真测试结果，从图7中可以看到，低频通带的中心频率为f1=1.64 GHz,3 dB相对带宽为4.24%，插入损耗为2.266 dB，回波损耗为15.39 dB；高频通带的中心频率为f2=2.54 GHz, 3 dB相对带宽为2.91%，插入损耗为2.97 dB，回波损耗为17.7 dB；双通带内的共模抑制保持在30 dB以下。低频通带的仿真与测试结果吻合良好，但高频通带的相对带宽有所缩减，这主要因为高频通带的耦合系数受谐振器间的缝隙控制，该缝隙在加工时存在一定的误差。

图6 电路实物照片Fig.6 Photograph of the fabricated circuit

图7 滤波器的测试仿真结果Fig.7 Simulated and measured results of the filter

表1给出了本文设计的滤波器与其他双通带滤波器的性能对比。可以看出，本文设计的滤波器双通带的频率、耦合系数以及外部品质因数都是独立可控的，与其他双通带滤波器相比，其设计灵活度具有明显的优势。

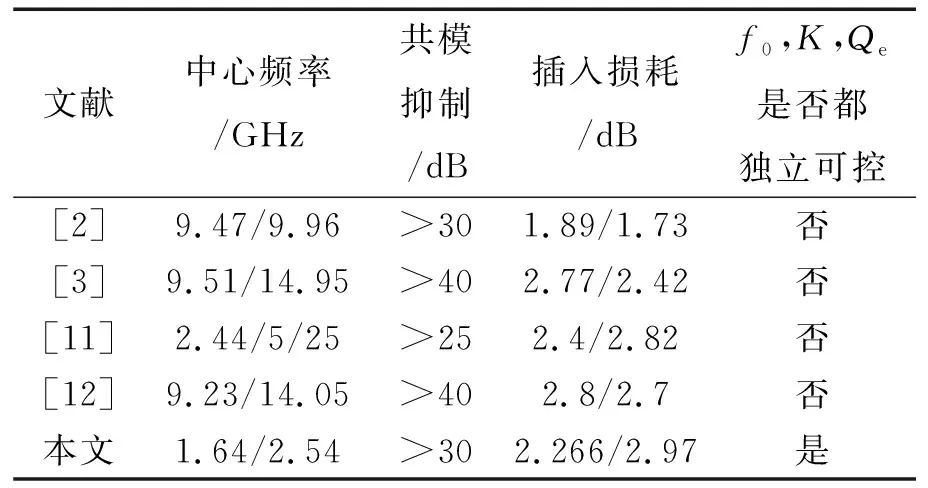
表1 本文设计与其他平衡式双通带滤波器对比情况Tab.1 Comparison of the proposed design with other balanced dual-band filters

4 结 论

本文提出了一种小型化的平衡式双通带带通滤波器，并且本文所提出的滤波器有很好的共模抑制能力、更加紧凑的尺寸，而且双通带的频率、耦合系数和外部品质因数都是独立可控的。该滤波器的仿真和测试的结果吻合良好。由于该滤波器具有很好的共模抑制能力和紧凑的尺寸，使得该滤波器能够适用于许多微波通信系统。