MIMO PLC系统中脉冲噪声消除方法
申 敏,李 想,林 欢
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 新一代宽带移动通信重点实验室,重庆 400065)
0 引 言
随着电力线通信(power line communication, PLC)技术的不断发展,为了满足更大容量和更快速率的需求,多输入多输出(multiple-input multiple-output, MIMO)信号处理技术开始应用在电力线通信中[1]。MIMO技术能够抵抗PLC系统信道的随机衰落,改善通信质量,且相比原来的单入单出(single-input single-output, SISO)PLC系统,MIMO PLC系统能够充分利用布线资源,在不增加频谱资源和发射功率的情况下,获得空间复用增益。目前ITU-T G.hn和HomePlug AV2标准中已经采用了MIMO技术[2]。但是PLC系统的发展还面临一些阻碍,主要的阻碍是系统存在脉冲噪声,脉冲噪声的功率谱密度比背景噪声高出50 dB[3],脉冲噪声会造成信号失真以及系统性能严重损失,因此,脉冲噪声的影响是PLC系统必须解决的问题。
目前国内外有许多研究者致力于PLC系统的研究,对脉冲噪声消除的方法提出了很多可行的方案。文献[4]提出用非线性方法消除脉冲噪声,通过设置最优的门限对超过门限的脉冲噪声置零或限幅处理。文献[5]提出基于压缩感知的脉冲噪声消除方法,该方法通过压缩感知技术重构脉冲噪声,但牺牲了频谱利用率,算法复杂度高。文献[6]提出了时频结合的迭代脉冲噪声消除方法,该方法应用在SISO PLC系统中,相比传统的时域消噪算法有良好的性能提升,但是脉冲噪声的虚警概率难以确定,使得该算法难以实现。本文主要研究MIMO PLC系统发射分集模式下的脉冲噪声消除方法。
本文所提算法主要将时频结合的迭代消噪算法运用到MIMO PLC系统中,并采用空频分组码(space frequency block code, SFBC)。空频分组编码利用PLC信道频率选择性衰落的特性获得频域分集,进一步提高性能。该算法通过在时域设置最优阈值对高幅度脉冲噪声置零;在频域采用空频分组码译码算法进行硬判决得到发射信号,采用空频分组码获得分集增益,使其在恶劣信道和噪声环境下依旧具有较好的译码性能,这保证了重构的脉冲噪声的准确性,能在时域消除重构的脉冲噪声,再通过多次迭代,可获得更好的性能提升。
1 MIMO PLC信道模型和脉冲噪声模型
1.1 MIMO PLC信道模型
家庭电力线路由相线P(phase wire),中线N(neutral wire)和接地保护线PE(protection earth wire)组成,这就为MIMO技术在家庭电力线通信中使用提供多端传输和多端接收的可能,但需满足基尔霍夫定律,所以发射端只能采用2根天线[1]。文献[7]利用多导体传输线理论(transmission line theory,MTL)和电压比方法(voltage ratio approach, VRA)来计算信道传递函数,构成MIMO PLC系统。MIMO PLC系统等效模型如图1所示。

图1 MIMO PLC信道模型Fig.1 MIMO PLC channel model
MIMO PLC信道传递函数为
(1)
(1)式中:Hb(f)为每个结点的电压,N表示节点的个数。
由于电力线拓扑结构特殊,供电网络大多数为相、中、地3条导线组成并具有相同的几何布局,根据电力线这种拓扑结构建立2×2 MIMO PLC系统的传输信道,并将传输信道分为N个节点,根据电压比计算Hb(f)。
V(xN-1)=HbV(xN)
(2)
(2)式中:V(·)表示节点的电压;xN表示第N个节点。
根据上述信道建模方法,得到本文采用的信道模型为
(3)
(3)式中,对角线上的元素称为共信道,非对角线上元素称为交叉信道。
1.2 脉冲噪声模型

ik=bkgk
(4)

nk=wk+ik
(5)
其概率密度分布为
(6)
(6)式中,G(·)表示高斯概率密度函数。
(7)
2 空频分组码编码原理
MIMO PLC系统信道具有频率选择性、衰减严重,且噪声环境复杂,为了保证通信的可靠性,可使用发射分集技术满足通信需求。空频分组编码是一种发射分集技术,该技术能够通过空间和频域分集,提高电力载波通信系统传输数据的准确性。空频分组码的基本原理是利用多个收发天线同时发射和接收,将每个发射分支进行空频编码,载频之间满足正交性,实现频率分集,可用于频率选择信道。
2.1 空频分组码编码
空频分组码编码常用Alamouti算法[9-10]。x(0)(i)和x(1)(i)是第1根天线的连续2个子载波上发射的信号,-x(1)(i)*和x(0)(i)为第2根天线的连续2个子载波上发射信号,如图2所示。将x(0)(i)记为x1,将x(1)(i)记为x2,在第k个子载波上从第1和第2个发射天线到第1根接收天线的信道系数分别用h11和h12表示,从第1和第2个发射天线到第2根接收天线的信道系数表示为h21和h22。

图2 SFBC编码原理Fig.2 SFBC encoding principle
接收天线i在第k个载波上接收到的信号为
(8)
2.2 空频分组码译码
空频分组码译码采用最大似然译码算法。接收端2根天线在第k子载波的接收信号可以写成
(9)
第k+1子载波的接收信号可以写成为
(10)
(11)
(11)式中,ΩNt为标准星座点集合,其中,Nt为发送天线的个数。

(12)
(13)
3 MIMO PLC系统中脉冲噪声消除算法
脉冲噪声在时域具有稀疏性,且幅度很大,在频域扩展到整个频带,不易捕获,所以脉冲噪声需在时域进行消除。传统的非线性消噪方法不能较好地消除脉冲噪声,因此,本文提出一种基于时频迭代的脉冲噪声消除算法并结合空频编码技术应用到MIMO PLC系统中。此算法分为2个部分:时域消噪和频域迭代消噪。时域消噪方法采用文献[8]的方法选择最佳门限对高幅度的脉冲噪声置零处理。频域迭代消噪方法是先进行硬判决检测,利用空频分组码空间和频域的分集增益,检测出更加可靠的符号;然后用频域接收信号减去重构信号得到重构时域脉冲噪声,最后在时域减去重构脉冲噪声,完成1次迭代过程。通过1次迭代后已经消除大部分脉冲噪声,再次迭代则系统性能将明显提升。算法原理如图3所示。
3.1 时域消噪
时域消噪的目的是消除幅度大的脉冲噪声,本文采用置零方法将高幅度脉冲噪声直接置零,文献[8]提出基于最大似然(maximum likelihood,ML)准则设置门限值。接收端接收到的信号为
rk=sk⊗h+nk
(14)

图3 接收端迭代脉冲噪声消除流程图Fig.3 Iterative impulse noise cancellation at receiver
当接收的正交频分复用(orthogonal frequency division multiplexing,OFDM)符号足够多时,rk可以用高斯分布来表示,这时概率密度函数为
(15)
(16)
依据判决规则,接收信号rk可分为无脉冲噪声的X1和有脉冲噪声X2这2种情况。根据ML准则,判决规则为
(17)
(17)式判决规则等价于
(18)
(19)
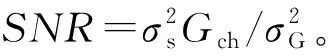
1.分析电路结构,弄清各电表测哪段电路的物理量。首先分析电路的结构,确定电路的连接方式,判断其为串联电路还是并联电路;这类问题中的电表多为理想电表,当电路中元器件较多且结构较为复杂时,首先对电路进行简化。电压表的阻值非常大,在电路中作开路处理,电流表的阻值非常小,在电路中作短路处理,这样电路中仅剩下电阻、开关、电源等基本电路元件,更容易搞清整个电路的电阻连接关系。其次弄清各电表测哪段电路的哪个物理量以及变阻器电阻变化的情况等。
此门限虽然能对高幅度的脉冲噪声置零,但是阈值不能设定过低,因为电力载波通信系统采用OFDM技术,峰均比较大,如果阈值过低容易消除幅度过高的有用信号,带来性能损失,所以低幅度的脉冲噪声需通过频域迭代来消除。
3.2 频域迭代消噪
经过时域消噪后,消除了高幅度的脉冲噪声,但是依旧存在低幅度脉冲噪声,所以频域消噪的目的是消除幅度较小的脉冲噪声。频域脉冲噪声消除充分利用SFBC的分集增益来重构出时域脉冲噪声,具体步骤如下。
步骤1SFBC译码。SFBC译码采用最大似然译码算法,由 (12) 式和(13) 式得
(20)
(21)
通过译码后的符号与标准星座点的欧氏距离进行硬判决,由于只存在低功率的脉冲噪声,OFDM系统能抵抗低功率噪声,加上SFBC编码能提高译码准确性,使硬判决过程不会造成大量的判错。
(22)
步骤2重构发射信号。对硬判决符号重新编码得到重构发射信号
(23)
将上述结果变换得到
(24)


(25)

(26)
此过程是重构剩余的脉冲噪声,门限值应设置相对较大,因为之前在时域已消除大部分脉冲噪声,所以剩下的脉冲噪声的数量较少,自适应门限表示为
(27)
步骤4消除脉冲噪声。通过步骤3后,重构出未被消除的剩余脉冲噪声,接下来用时域消噪处理后的接收信号减去这部分重构的脉冲噪声,达到频域消噪目的。
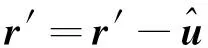
(28)
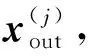
本文所提算法相比于传统消噪算法增加了频域迭代消噪的步骤,主要包括空频分组编译码、2个快速傅里叶变换和重构脉冲噪声的复杂度,其空频分组编译码的复杂度为NtNrKNt,其中,Nr为接收天线的个数,重构脉冲噪声复杂度为NrN,傅里叶变换的复杂度为NtNrNFFTlbNFFT,其中N为子载波个数,NFFT为采样点数,K为调制阶数,迭代次数为L,总的复杂度为L(NtNrKNt+NrN+NtNrNFFTlbNFFT)。相比其复杂度有所增加,但其性能提升明显。因此,迭代脉冲噪声消除方法能最大程度地消除脉冲噪声对系统性能的影响。
4 仿真结果分析
为了验证本文所提算法的可行性,通过MATLAB仿真对比置零法、限幅法和本文提出的脉冲噪声消除算法的性能以及不同迭代次数的仿真性能。
本文的仿真环境参考文献[7],仿真参数如表1所示,用2×2 MIMO PLC信道建模,参考文献[8]建立脉冲噪声模型,如图4所示,采用16QAM调制方式,信道编译码采用Turbo码。
所提算法和传统算法仿真对比如图5所示。图5对比了采用本文所提算法1次迭代、置零法、限幅法、无脉冲噪声情况和未消除脉冲噪声情况下的仿真性能。在未消除脉冲噪声情况下,仿真性能很差,因为受到脉冲噪声的影响,在很高的信噪比下误码曲线也很难趋近于零;限幅法比在未消除脉冲噪声情况下的性能可以提升2 dB以上,表明该算法能消除部分脉冲噪声;而置零法比限幅法的性能提升了0.8 dB,这是因为置零法的门限一般较限幅高,不会将高幅度的有用信号置零;本文所提算法比置零算法的性能提升0.15 dB,但由于1次迭代未能完全重构脉冲噪声并消除,性能提升不够明显。

表1 仿真参数

图4 脉冲噪声Fig.4 Impluse noise
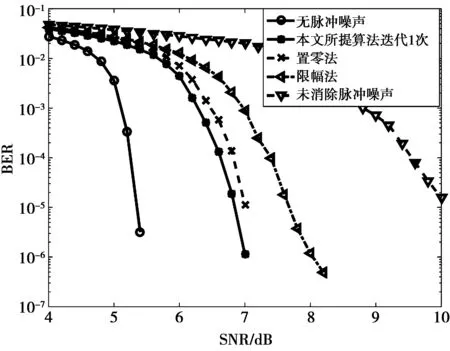
图5 所提算法和传统算法仿真对比Fig.5 Performance comparison between proposed algorithm and traditional algorithms
不同迭代次数误码率对比如图6所示。图6给出本文所提算法在不同迭代次数下的仿真对比,包括在无脉冲噪声情况下、本文所提算法迭代1次、迭代2次和迭代4次。经过1次迭代的性能已经优于传统的消噪算法;2次迭代比1次迭代性能提升1.31 dB,因为经过1次迭代后已经消除大部分脉冲噪声的影响,再通过SFBC译码能够判决出更加准确的发射符号,性能提升明显;4次迭代与2次迭代性能相差不大,性能提升趋缓,由此可见,迭代算法无需多次迭代,算法复杂度并不高,而且能消除脉冲噪声的影响提升MIMO PLC系统的性能。

图6 不同迭代次数误码率对比Fig.6 BER comparison of different iterations
5 结束语
本文提出应用于MIMO PLC系统的迭代脉冲噪声消除算法。该方法结合时域和频域消噪并利用SFBC的分集增益能够得到良好的性能提升。脉冲噪声在时域具有稀疏性,基于ML准则设置最优门限对时域高幅度的脉冲噪声置零,再通过SFBC编码获得分集增益能够准确地重构出时域脉冲噪声,经过2次迭代消除脉冲噪声。仿真表明,本文所提算法较传统脉冲消除算法有明显的性能提升,而且迭代次数少,便于工程实现。

