IBM模型对偶偶核的研究

董鸿飞

（赤峰学院 物理与电子信息工程学院，内蒙古 赤峰 024000）

1 引言

在原子核结构的研究过程中，出现了多个理论模型.相互作用玻色子模型（interacting boson model，简称为IBM）就是一个重要的研究原子核集体运动的代数模型，在描述核的能谱结构方面取得了很大成功[1].在IBM中，价核子或空穴对可以看作是具有角动量L为0的s玻色子和L为2的d玻色子.s玻色子和d玻色子张开的空间可以用一个六维群U(6)来描述，它可以约化为三个子群链：

这三个子群链分别对应于不同类型的动力学对称性，用来描述核的三种集体运动极限：振动、转动和γ-不稳定特性[2-7].

基向量可表示为 |Ψ〉=|nd,nβ,nΔ,Ld,L〉，将哈密顿量写成多极展开形式为：

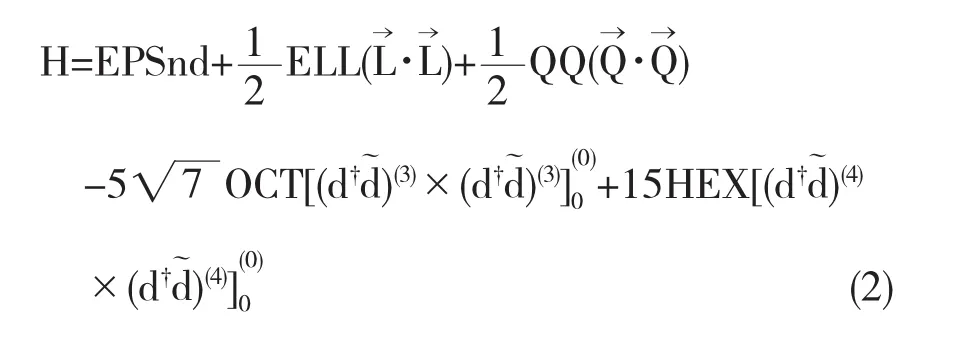
其中：

这里 EPS、ELL、QQ、OCT、HEX、CHQ 为参数[8].确定这几个参数是一个相当棘手的过程，需要大量的计算，将计算结果与实验数据进行对比，直到理论值与实验值良好拟合.

2 计算结果

2.1 能谱

图1 的实验能谱

理论计算得到的能谱与实验能谱的对比图为

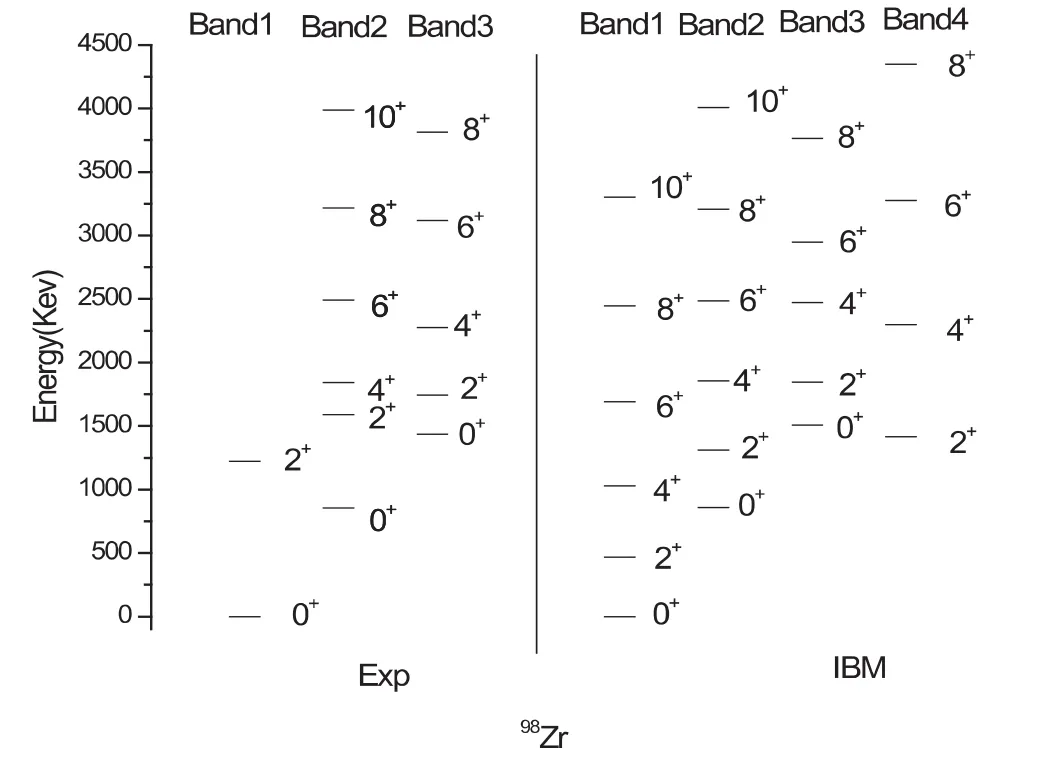
图2 的理论能谱与实验能谱

2.2 参数

得到以上能谱所用的参数为：

表1 的哈密顿参数

表1 的哈密顿参数

EPS ELL QQ OCT HEX CHQ-0.3901 0.0092 -0.0438 0.0593 0.0049 -1.5980

2.3 波函数

主要状态的波函数的结构为：

2.4 电磁跃迁

表2 的电磁跃迁

表2 的电磁跃迁

跃迁能级 B(E2) 跃迁能级 B(E2) 跃迁能级 B(E2)21+→01+ 21.5696 22+→02+ 12.4804 24+→03+ 4.7098 23+→11+ 29.5229 31+→13+ 22.8614 41+→21+ 29.5559 42+→22+ 16.8138 43+→23+ 17.0739 44+→24+ 5.0221 43+→41+ 15.4456 51+→31+ 17.0788 61+→41+ 32.4357 62+→42+ 17.9246 64+→43+ 22.1803 63+→44+ 6.9730 64+→61+ 10.3508 71+→51+ 21.0443 81+→61+ 32.5311 82+→62+ 16.9602 83+→63+ 3.4003 84+→64+ 23.3241 84+→81+ 7.3655 91+→71+ 20.8522 101+→81+30.6896 102+→82+14.8110 103+→83+ 7.2371 104+→84+22.0295

3 结论