基于Matlab的小波变换图像压缩算法研究

关雪梅

（辽宁对外经贸学院 基础课教研部，辽宁 大连 116052）

1 引言

随着信息化技术的快速发展，各行各业越来越多的数字信息需要被存储，被保留，海量数据处理面临着很大的难题，因而越来越多的学者开始着手于数字信息压缩处理的研究，数字图像压缩技术也是研究的热点之一.图像压缩技术是图像处理领域中需要研究的一个非常重要的问题，数字图像在传输处理的过程中会出现各种冗余的信息，数字图像压缩技术的目的就是保留图像的有用信息，消除图像中存在的冗余.小波变换技术进行图像压缩一般采用的是多尺度分析方法，可以对每个层次的系数进行变换的处理，这样就可以得到极高的压缩比.

Matlab是一种用于数学计算和计算机图像处理的应用软件，它具有图像信息处理、矩阵运算、数值分析等多种功能，用户界面和设计环境友好，为工程的应用和科学理论研究做出了巨大贡献，是一种非常好的程序开发工具.本文主要是在Matlab软件环境下采用小波变换的方法进行数字图像压缩处理，既快又准确地完成数字图像的压缩工作.

2 小波分解与小波重构

小波变换是基于时间、空间和频率的一种图像处理的局部变换方法，采用水平移动和伸缩的方法进行函数多尺度运算，可以实现在图像的低频率处使频率进一步细分，图像高频率出使时间进一步细分.通常采用二维离散小波变换进行图像压缩，分别在垂直和水平方向进行高通滤波和低通滤波处理，做下采样，原始图像小波分解图如下图所示：

在上图中A表示低频分量，B表示高频分量，下标1和2分别代表一级或二级分解.

原始的数字图像在经过二维离散小波变换处理后，获得许多具有不同分辨率的子图像，这些子图像含有的频率是不一样的.很多含有高频的子图像数据点都靠近0，而且是越高这种现象越明显.分辨率为n的数字图像通过二维离散小波变换可以将其低频成分逐步分解为分辨率为n+1斜线、垂直、水平的高频部分和低频部分.三个方向的高频部分保持不变，低频部分继续依照上述方法继续分解，从而实现数字图像的多分辨率的分解，分解过程如下图所示：

图2 二维小波变换分解图

由此可推断出小波重构算法，二维小波重构如下图所示：

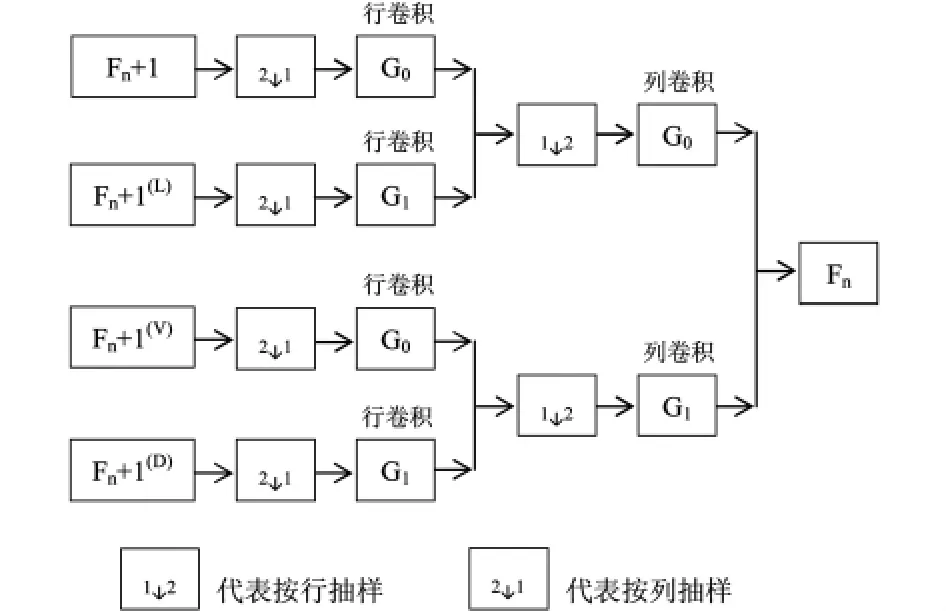
图3 二维小波变换重构图

其中，L0L1分别表示分解的低通和高通滤波器，G0G1分别表示合成后的低通和高通滤波器.

3 小波变换用于图像压缩

数字图像通过小波变换方法进行图像压缩基本设计思想是将原图像进行多分辨率分解处理后，分解成很多频率和空间都不相同的子图像，接着再进行子图像系数编码处理.采用小波变换的方法进行图像压缩处理的重点就是系数编码，对子图像系数进行量化的压缩.由于小波变换自身是不含有图像压缩功能的，所以通过小波变换处理过的数字图像和原图像的数据总量是保持不变的.我们采用小波变换进行数字图像压缩处理是由于最终生成的图像和原始图像不同的特点，在图像的低频部分能量集中表现，图像对角线、垂直和水平部分能量表现较少.而图像在对角线、垂直和水平部分的边界信息比较突出，有很明显的方向性.前者我们可以称之为亮度图像，而后者称之为细节图像.最终可以获得4个子图像，经过分析人的心理和视觉特点，对子图像进行编码量化处理.由于人对亮度敏感的视觉特点，在进行图像压缩处理时尽量避免失真的效果.

Matlab是一种效率很高的数据处理软件，在图像处理、数值运算、自动控制、金融分析等方面应用非常广泛.Matlabe进行数字图像处理的第一步是使用变换的小波基对灰度图像进行处理，接着进行全局范围的阈值压缩处理，之后进行图像分层阈值压缩处理，最后执行小波包全局化阈值压缩，获得最终压缩图像.

4 Matlab实现

数字图像进行小波变换分解后，可以获得若干个分辨率不同的子图像，这些分解后的子图像有不同的频率.拥有高频分量的子图像的数据大部分接近零，清晰度越高效果越明显.往往对一副数字图像来说最有代表性的是它的低频数据，因而图像的压缩方法是经过小波分解后，保留图像的低频数据而去除图像的高频数据.使用Matlab软件进行小波变换图像压缩的具体方法如下：

load p1；%载入图像

subplot(2，2，1)；image(X)；colomat(map)；

title(‘原图像’)；%将原图像显示出来

disp(‘原图像X尺寸：’)；whos(‘X’)；

[m，n]=wavedec2(X，2，‘bior3.7’)；%采用 bior3.7 小波对原图像进行二层分解

f1=appcoef(m，n，’bior3.7’)；%获取小波分结构的一层低频及高频系数

t1=detcoef2(‘h’，m，n，1)；%水平方向（其他方向与此相似）

hh1=wrcoef2(‘h’，m，n，‘bior3.7’，1)；%将第一层水平数据进行重构处理（其他方向与此相似）

f1=appcoef2(m，n，‘bior3.7’，1)；

f1=wcodemat(f1，440，‘mat’，0)；%将小波分解后的第一层低频信息保留并进行图像压缩，同时量化编码

f2=appcoef2(m，n，‘bior3.7’，2)；

f2=wcodemat(f2，440，‘mat’，0)；%将小波分解后的第二层低频信息保留并进行图像压缩，同时显示出来

经过Matlab实验，采用小波分解方法将原图像进行第一次压缩是获取第一层中低频数据，压缩约为三分之一的数据含有量，压缩效果较理想.接着继续第二次压缩，获取第二层低频数据，压缩为十二分之一的数据含有量，压缩效果也还可以.由此可见，采用小波变换方法进行图像压缩处理不需要进行其他操作就可以获得比较满意的压缩效果，是一种非常好的图像压缩方法.

5 结束语

数字图像压缩技术是非常有发展前景的领域，影响着社会多个行业.数字化信息时代必然会产生大量的图文数据，因而人们越来越重视图文压缩算法的研究.采用小波变换方法可以很好地对图像进行压缩，小波变换多频段分解压缩的基本原理符合人类视觉多频率通道的特征，因而可以利用人类视觉上的这一特性进行图像压缩数据处理.本文采用Matlab的相关函数和处理算法来实现小波变换图像压缩，对于一般的图像来说，通过变换可以获取较大的图像压缩比，处理后的图像清晰度高，图像效果好，基于Matlab的小波变换图像压缩算法有很好地应用前景.