一类带时滞的Lotka-Volterra竞争扩散模型周期解的收敛性质研究

陆求赐，王学彬

（1.武夷学院 人文与教师教育学院；2.武夷学院 数计学院，福建 武夷山 354300）

1 引言

Lotka-Volterra模型是一个微分动力学系统，最初由Lotka(1925年)和Volterra(1926年)各自提出，用于模拟生态学中种群的动态关系，之后经济学家用它来描写宏观的增长波动以及描写中观的规模和范围经济层次的市场竞争(见[1]及它的参考文献).同时该模型也用于描述草地生态系统，探讨系统内牧草种群与放牧家畜种群之间的关系，正确指导草地畜牧业可持续发展具有一定意义[2].因此Lotka-Volterra模型在生态学及经济学领域都有着广泛的应用.本文根据Holling–Tanner两种竞争种类相互作用的假设[3]，考虑如下一个带时滞的扩展的Lotka–Volterra竞争扩散模型：

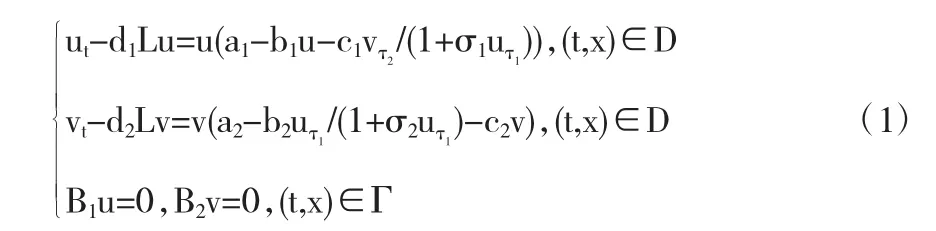
为研究需要，本文还需考虑如下周期性和初值条件：

其中ηi(t,x)，i=1,2是给定的初值函数.

本文在研究时一般是模型问题(1)加上一个条件(2)(当m=1时)或者条件(3)，下面就直接写成问题(1)(2)或者问题(1)(3).

2 预备知识

引理1令λi(ai)和øi(t,x)，i=1,2是如下问题的特征值和它正的对应的特征函数：

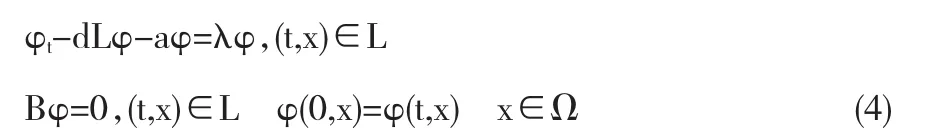
其中 L=Li，B=Bi，a=ai，d=di，i=1,2. 根据标准的抛物方程理论，容易从上面的问题(4)的讨论中看出：如果λi(ai)≥0，i=1,2的话，问题(1)仅有一个平凡解(0,0).而如果 λ1(a1)＜0且λ2(a2)≥0(或者 λ1(a1)＞0 且 λ2(a2)＜0)的话，则问题(1)也有半平凡的T-周期解(即周期为T的解，下同)(U,0)(相对应于(0,V))，其中U和V是对应于问题(1)中不含时滞项的如下问题的正的T-周期解：

由此，可得到如下引理：

引理2问题(1)(2)的一个正的T-周期解的存在的一个必要(非充分)的条件是 λi(ai)＜0,i=1.

定义1(比较原理) 如果)满足下式，则称)是问题（1）的上解：

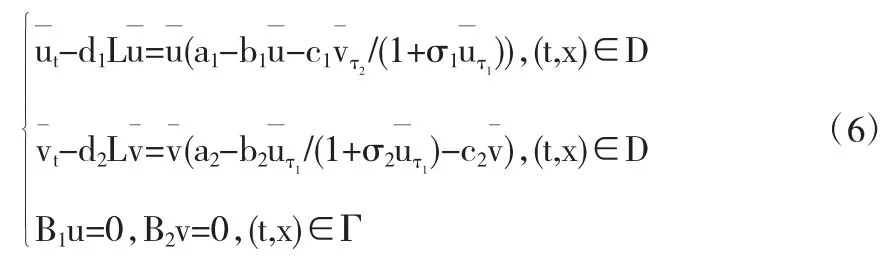
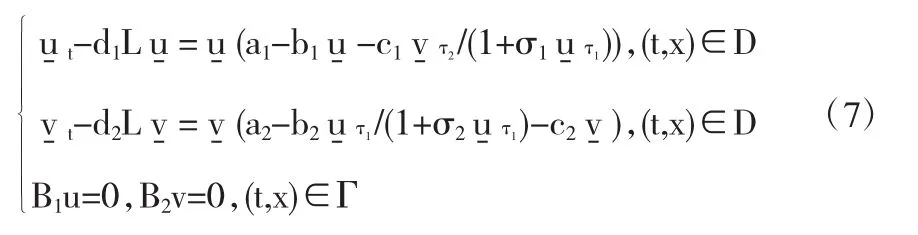
定义 2(解的收敛性) 令(u(t,x；η1)，v(t,x；η2))是问题(1),(3)具有(η1,η2)其中 ηi(0,x)≢0,i=1,2 的解，而且如果满足下式：

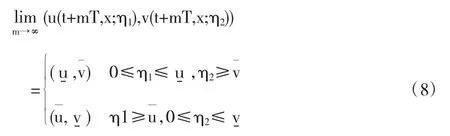
则称解(u(t,x；η1)，v(t,x；η2))具有收敛性.

3 主要结论及证明

定理 1 令(u(t,x；η1)，v(t,x；η2))是问题(1)(3)的具有(η1,η2)其中ηi(0,x)≢0，i=1,2的解，并且满足下面条件：

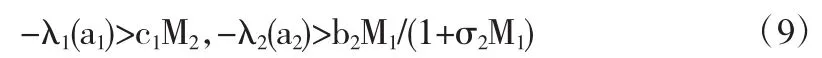
这里c1=c1(t,x)，b2=b2(t,x)为上是光滑的T-周期函数，M1,M2满足下面关系：

那么有：

（2）问题(1)(3)的解(u(t,x;η1),v(t,x;η2))具有收敛性质(8)；

证明（1）要证明问题的存在性，我们需要考虑下面抛物边值问题：

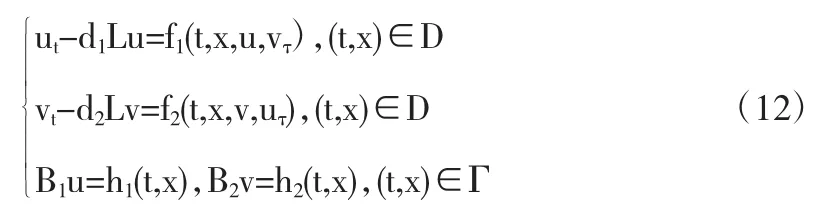
现在令w=M-v(M为一个充分大的常数)来做转换，那么问题(1)可以转化为问题(12)具有 u=(u1,u2)≡(u,v)，f=(f1,f2)，(h1,h2)=(0,Mβ)的形式，其中 β=β(t,x)为 Γ 上的 Holder连续的函数，而且(f1,f2)具有如下形式：

容易看出上面的函数(f1,f2)在S×Sτ上是拟单调非增的，其中S×Sτ=R+×[0,M].因此，对于一个正的T-周期解的存在性能够从上面的转换问题中发现一对标准的上下解，我们找到如下形式的一对解：

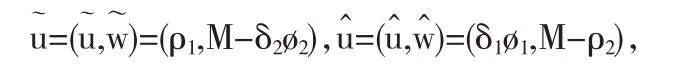
这里 ρi与 δi(i=1,2)为正的常数，其中 ρ2＜M，且 ρ2、δi(i=1,2)足够小.

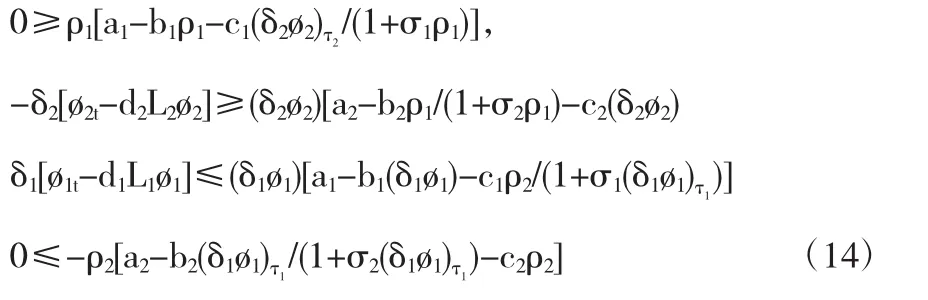
再根据特征值问题(4)及标准的抛物方程理论，则上面的不等式(14)对于一些充分小的δ1,δ2还是会成立的，如果下面的式子(15)成立的话：

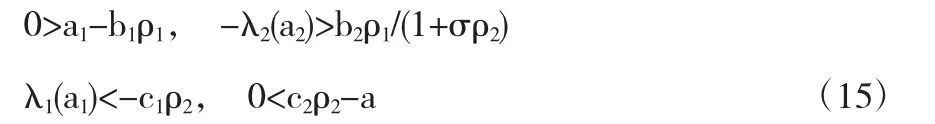
又因为条件(10)成立，这就证明了在条件(9)下，问题(1)(2)的转换问题有一个最大化的T-周期解和一个最小化的T-周期解(u,w)，使得：

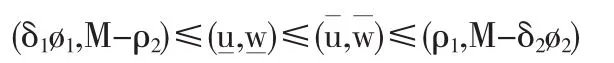
而且，根据文[4]中的定理3.1，初边值问题(1)(3)的解u≡(u,w)具有形如(η1*,η2*)≡(η1,M-η2)的收敛性质，现在通过转化v=M-w，则与（其中是周期性边值问题(1)(2)的一对正的T-周期解，而且满足下面的关系：

（2）根据上面步骤(1)的证明，进一步地有，对于任意在D0(i)=[-τi,0]，i=1,2 上满足 δ1ø1≤η1≤ρ1，δ2ø2≤η2≤ρ2关系的(η1,η2)，初边值问题(1)(3)的解是由(u,v)≡(u,M)给出，并且在 D上满足关系 δ1ø1≤η1≤ρ1，δ2ø2≤η2≤ρ2.

对于任意非负且具有 ηi(0,x)≢0,i=1,2 的(η1,η2)，一个在(u,v)与问题(5)的(U,V)(与(η1,η2)一样)之间的比较表明：在[t0,+∞)×(对于某些 t0≥0)上有(u,v)≤(U,V).由于(U,V)＜(ρ1,ρ2)而且(δ1,δ2)＞(0,0)可以被选任意小，我们可以看出存在 t*＞0 与(δ1,δ2)＞(0,0)，使得

δ1ø1≤η1≤ρ1，当 t*-τ1≤t≤t*时

δ2ø2≤η2≤ρ2，当 t*-τ2≤t≤t*时（x∈Ω）

再根据文[4]中的定理3.2，解(u,v)具有收敛性质：

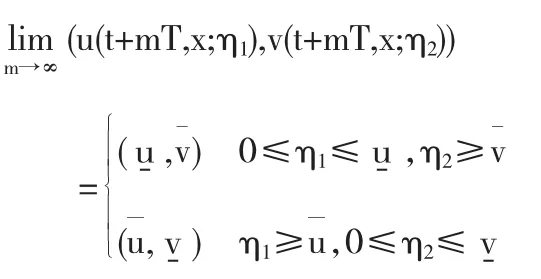
（3）u(t+mT,x;η1)和 v(t+mT,x;η2)的极限可以分开证明，根据上下解的性质和解的收敛性质，这里先证=u*(t,x)成立：

考虑到当 0≤η1≤u 时，u(t+,x;η1)可作为问题(1)(3)的一个上解，现令

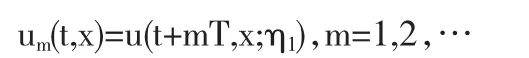
则有 um(t,x)=u(t+mT,x;η1)≤(t+mT,x;η1)=(t,x)，m=1,2，…

另一方面，根据文[4]中的引理3.2有u(t+mT,x;η1)≥(t,x)，因此可以得到：

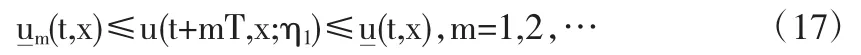
我们再考虑到当 η1≥u 时，u(t,x;η1)可作为问题(1)(3)的一个下解，则有

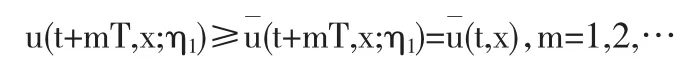
根据上下解的性质有u(t+mT,x;η1)≤(t,x)，因而可以概括得到：