基于LINDO的会议筹备问题多阶段决策模型

宿 曈

（西北民族大学 数学与计算机科学学院，甘肃 兰州 730000）

1 问题的提出（2009年全国大学生数学建模竞赛题D，数据从略，文字有修改）

某市一家会议服务公司负责承办某专业领域的一届全国性会议，会议筹备组要为与会代表预订宾馆客房，租借会议室，并租用客车接送代表.由于预计会议规模庞大，而本市适于接待这次会议的几家宾馆的客房和会议室数量均有限，所以只能让与会代表分散到若干家宾馆住宿.为了便于管理，除了尽量满足代表在价位等方面的需求之外，所选择的宾馆数量应该尽可能少，并且距离上比较靠近.

筹备组经过实地考察，筛选出10家宾馆作为备选，它们的名称用代号1至10表示，10家宾馆有关客房和会议室的规格、间数、价格等情况及其相对位置均已知.

虽然本届会议代表返回了会议回执，但从以往几届会议情况看，有一些发来回执的代表不来参会，同时也有一些与会的代表事先不提交回执，因此筹备组面临的第一项任务是预测参会人数.

尽管客房房费由与会代表自付，但是会议筹备组要为与会代表预订宾馆客房，如果预订客房的数量大于实际用房数量，筹备组需要支付一天的空房费，而若出现预订客房数量不足，则将造成非常被动的局面，引起代表的不满.预订宾馆客房的数量是筹备组要解决的第二项任务.

按照会议安排，会议期间有一天的上下午各安排6个分组会议，筹备组需要在代表下榻的某几个宾馆租借会议室.这是筹备组要解决的第三项任务.由于事先无法知道哪些代表准备参加哪个分组会，筹备组还要向汽车租赁公司租用客车接送代表.现有45座、36座和33座三种类型的客车，租金分别是半天800元、700元和600元.如何租赁汽车是筹备组要解决的第四项任务.

本文利用本次会议与会代表的回执信息和历届会议的历史数据，就会议筹办中诸环节的决策分四个模块——预测参会人数、预订宾馆客房、租借会议室、租赁汽车等方面给出多阶段决策模型，利用动态规划解法，就上述问题在各阶段上或用多目标规划，或用单目标规划，并利用优化软件Lindo给出各阶段的最优解，从而得到整体最优解.

2 模型假设与简化

1.参会人员的个人特征为性别，仅用于安排住宿，而与其他方面毫无关系.故在估计参会代表的男女比例时，以收到回执的男女代表人数进行估算.

2.本届会议的参会代表与历届参会代表可以看作是来自同一母体的不同样本，样本容量不同，故可考虑用往届与会代表的统计数据来估计本届参会代表的情况，如发来回执但不参加会议的代表数的概率等.

3.所讨论的母体中每一个体是否参会是独立的，设本次参会人数为ζ,它是一个服从参数为λ的Poisson分布p(λ)，其中λ是预测的参会代表的平均人数.

4.为讨论简化，以点来代表宾馆，以宾馆7为原点，以宾馆6和7所在直线为横轴（由6指向7的方向为正方向），以宾馆7和5所在直线为纵轴（由7指向5的方向为正方向）建立平面直角坐标系，则各宾馆位置如下：宾馆1(300,0)，宾馆 2(450,0)，宾馆 3(1000,-200)，宾馆 4(950,0)，宾馆 5(0,300),宾馆 6(-300,0)，宾馆 7(0,0)，宾馆 8(0,-200)，宾馆9(-150,-200)，宾馆 10(-1000,0).

另外定义两宾馆i(xi,yi)，j(xj,yj)间距离为：

于是对于宾馆之间的距离可整理出来（此处略）.

5.假设本市同价位的客房间服务、设备配置等无差异，不同宾馆间容纳人数相同的会议室间服务、设备配置等也无差异，只是租赁价格不同.

6.本次会议纯属学术会议，不涉及其他部门的其他事务，也不考虑机场、车站等与入住宾馆间的远近、便利等其他因素，只考虑入住的床位与入住后参加分组会议的便利情况.

7.本届会议均可预定各宾馆所有的客房和会议室.也假设市内交通畅通无阻，不考虑红绿灯等其他影响交通的因素，并且代表上下车、车辆停靠等不花费时间.

8.下文用到的一些符号及说明ti——预订i宾馆的情况，则

xij——预订i宾馆j种客房的数量，i=1，2，…，10，j=1，2，…，16，xij≥0 为整数

cj——j类客房可容纳的最大人数

pj——j类客房每天的价格（单位：元/间·天）

qij——客房xij的数量，其中i=1，2，…，10，j=1，2，…，16

Q——本次会议需要预订客房的人数

wij——i=1，2，…，10，j=1，2，…，9时j类客房可以安排一人住宿

通过前面分析，我们的任务是利用某次会议与会代表的回执信息，预测参会人数，为与会代表预定适量的宾馆客房、租借适量的便利的会议室、租赁适量的某种规格的汽车接送代表，因此我们认为这是一个多阶段决策问题，构造一个多阶段决策的数学模型，在各阶段上或用多目标规划，或用单目标规划，并利用优化软件Lindo给出各阶段的局部最优解.

3 会议筹备的多阶段决策模型及求解

根据我们的目标，要求预订的宾馆数尽可能少，有目标约束

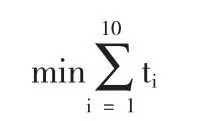
又要求预订的宾馆在距离上尽可能靠近，有目标约束

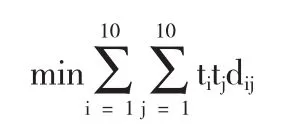
而参会代表希望客房价位比较合理，有目标约束

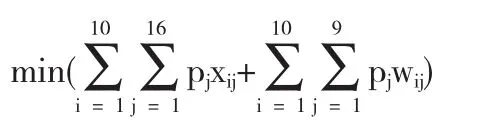
于是，我们的数学模型为下列多目标规划模型：

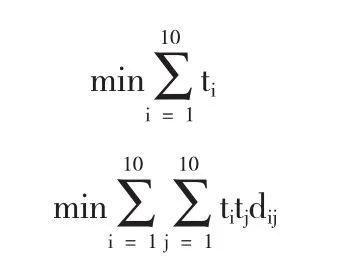
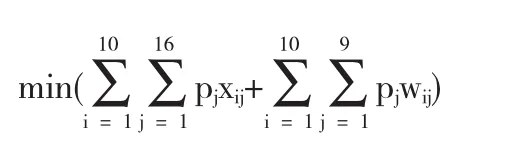
约束条件为

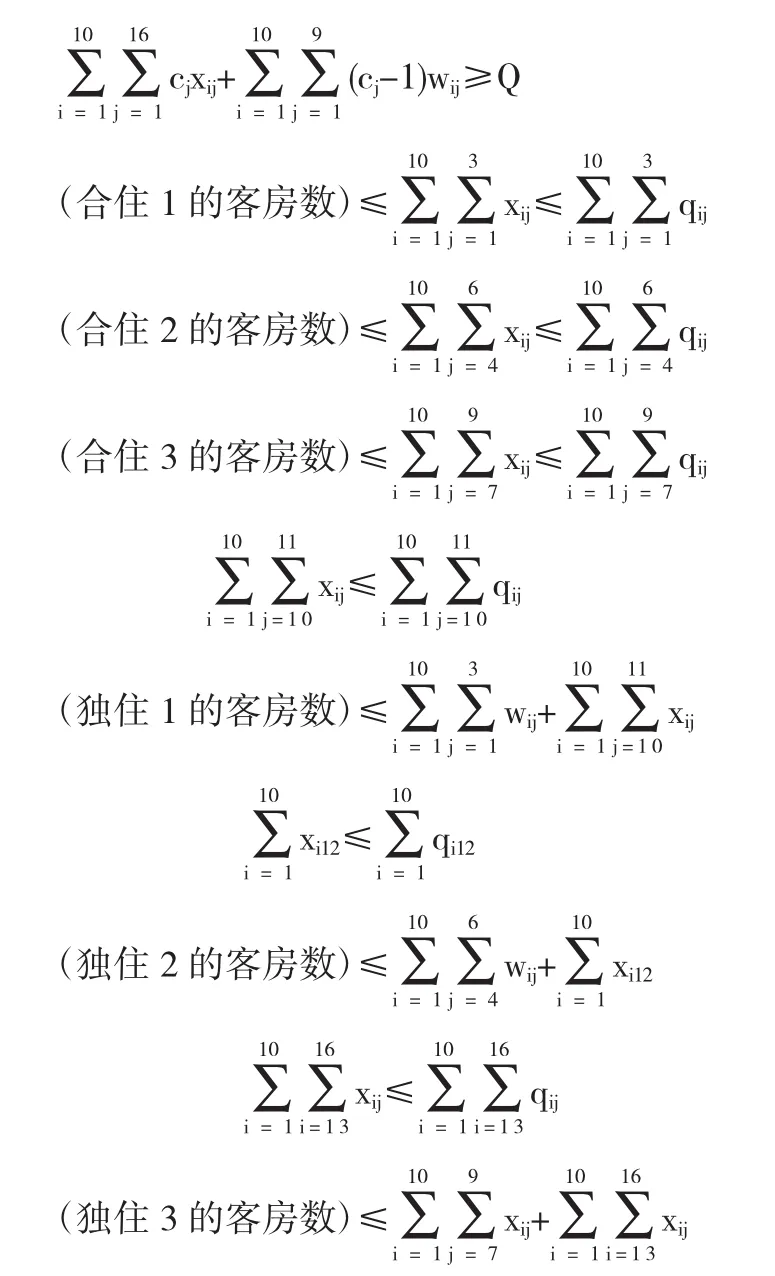
0≤xij≤qij，为整数，i=1,2,…，10，j=1,2,…,16

wij≥0，为整数，且 xij+wij≤qij，i=1，2，…，10，j=1，2，…，9，ti=0 或，i=1，2，…，10

第一阶段决策——确定参会人数

求解多目标规划模型有很多的方法，根据我们研究问题的特点，我们选用分层序列法，即将目标函数按其重要程度排成一个次序，然后在前一个目标函数最优解的基础上，求后一个目标函数的最优解，每次求解一个单目标规划模型.为解此模型，我们先来估计参会代表的人数.

根据本类会议往届参会代表的统计情况，我们用加权平均的方法估计本届会议中提交回执但不与会的人数比例r1及不提交回执而与会的人数比例r2，从而预测参会代表的平均人数.

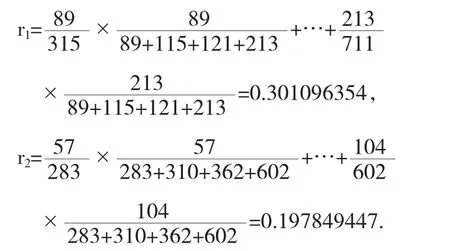
故本届会议中提交回执但不与会的人数估计为755r1=227.3277476≈227，而不提交回执而与会的人数设为x，则有

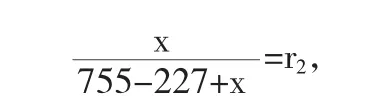
则x=130.2305504，于是估计本届会议与会人数为755–227+131=659人.

根据假设3，预测的参会代表的平均人数λ=659，参会人数ζ服从参数λ=659的Poisson分布，由于参会人数较多，根据大数定律的极限定理，ζ近似服从均值为659，方差为659的正态分布.为了节约经费及避免被动，于是我们想以较大的概率（如90%以上）的保证与会代表能够住到预订的客房内，由于Φ(1.29)=0.90147，于是

即ζ=692.1155839.这样需要我们按照693人来预订客房.

第二阶段决策——确定宾馆及客房类型与数量

根据本届会议的回执情况估计各类客房的预订人数.由假设1，对回执中预定各类客户的人数乘以系数并取不小于它的整数即得，于是我们所要求解的问题是确定下列模型中的 ti，wij，xij.

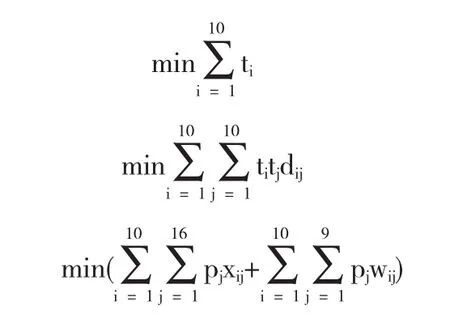
约束条件为

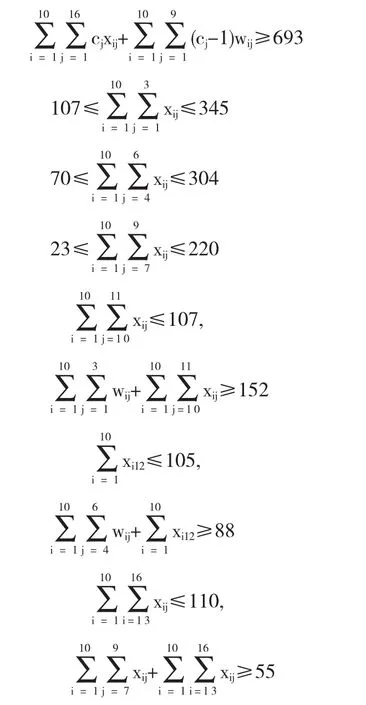
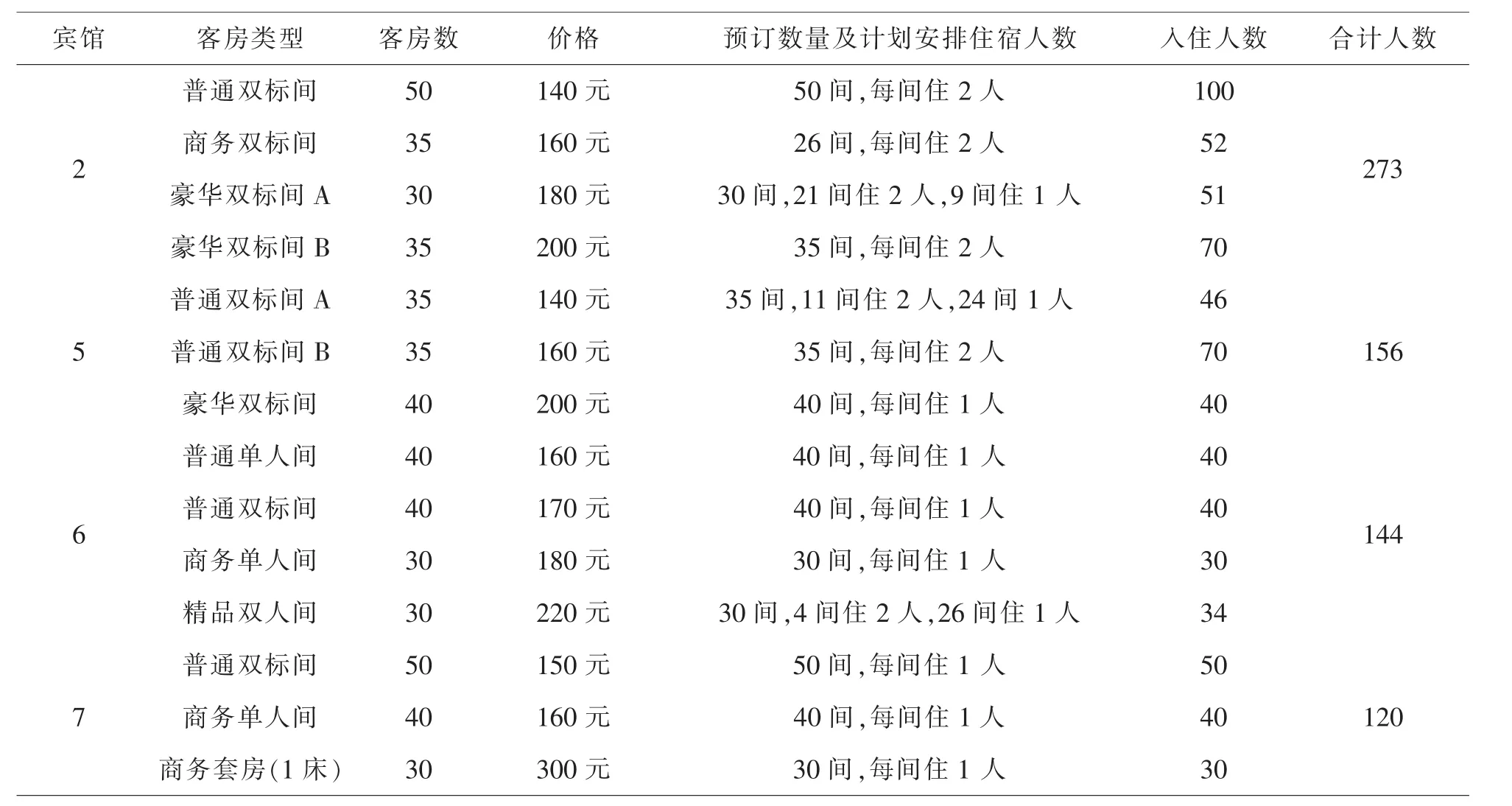
宾馆 客房类型 客房数 价格 预订数量及计划安排住宿人数 入住人数 合计人数普通双标间 50 140元 50间，每间住2人 100 2商务双标间 35 160元 26间，每间住2人 52豪华双标间A 30 180元 30间，21间住2人，9间住1人 51豪华双标间B 35 200元 35间，每间住2人 70 273普通双标间A 35 140元 35间，11间住2人，24间1人 46 5普通双标间B 35 160元 35间，每间住2人 70豪华双标间 40 200元 40间，每间住1人 40 156普通单人间 40 160元 40间，每间住1人 40 6普通双标间 40 170元 40间，每间住1人 40商务单人间 30 180元 30间，每间住1人 30精品双人间 30 220元 30间，4间住2人，26间住1人 34 144普通双标间 50 150元 50间，每间住1人 50 7商务单人间 40 160元 40间，每间住1人 40商务套房（1床） 30 300元 30间，每间住1人 30 120

0≤xij≤qij，为整数，i=1，2，…，10，j=1，2，…，16

wij≥0，为整数，且 xij+wij≤qij，i=1，2，…，10，j=1，2，…，9

ti=0 或 1，i=1，2，…，10

利用Lindo优化软件，可得如下结果，即宾馆选择2、5、6、7四家即可，客房类型与数量如下表：

第三阶段决策——确定宾馆的会议室及数量

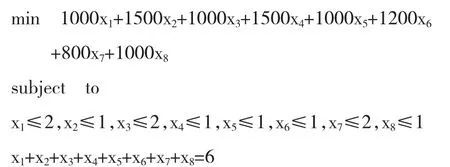
x1≥0,为整数.

利用Lindo优化软件，解得租用会议室的费用为5600元，结果如下：

宾馆 会议室容量 会议室价格 租借数量5 150人 1000元 2 6 160人 1000元 1 7 140人 800元 2 200人 1000元 1

第四阶段决策——确定租借车辆的情况

整理各宾馆中的所住代表人数情况，于是可确定由宾馆i→j的乘车人数.为了让每一个不在所住宾馆参加分组会的人都有车乘，用xij,yij,zij分别表示租借用天宾馆i到j的车型 x（45座）、y（36座）、z（33座）的数量，注意到在宾馆 2没有租用会议室，则可建立如下模型：

利用Lindo求解，可得租借车辆的费用为22000元，具体派车如下：

i→j的派车情况 5 6 7 2 45座1辆 ，33座1辆 45座1辆 45座2辆，33座1辆5 0 33座1辆 45座1辆，33座1辆6 33座2辆 0 45座2辆7 33座2辆 33座1辆 0

4 模型的说明

从模型的建立与求解的过程可知，我们在估计人数，安排住宿方面都达到了代表的要求（以90%的概率），现在只需改进租车方案.从生活经验可知，在450米距离内租车是没有必要的.因此通过计算，宾馆2与7之间、5与7之间、6与7之间是不需用车的，这样我们的方案就可以减少8辆车，一天的租车费用降为8800元，降幅达60%，节约的这部分费用足够租赁本次会议所需的会议室，并且还可节余2000多元.

从所给模型的规模及可解性来看，该模型无论从理论方法上还是技术手段上，在讲究决策科学化，办公自动化的新时代，都为会议筹备人员提供了一种有效的帮助.另一方面，我们也看到：没有高效的办公软件，没有专业的工具软件，对这种规模问题的求解是欠效率的，即使求得结果，也是让人怀疑其正确性的.因此在未来大数据时代、云计算时代，必须具备一定的数据处理能力，所以本模型具有一定的可移植性，具有实用价值和推广价值.