公寓门禁运行流程的Petri网模型优化分析

胡 源，王丽丽，刘祥伟

（安徽理工大学 数学与大数据学院，安徽 淮南 232001）

1 引言

近年来，科学技术的不断进步与发展，公寓自动门禁的功能也日益完善，但是由于现代公寓人员流动环境的复杂性，导致了公寓门禁管理系统在限制人员进出时有着很多缺陷，因此如何设计优化门禁管理系统模型是整篇文章的重点.

目前，国内外许多学者都在行为轮廓以及建模优化方面进行研究.在文献[1]中介绍了Petri网的相关定义和基本概念，并且利用相关的概念定义来对实际生活中的系统进行基于Petri网来建立的模型，并且能够准确地分析业务流程的可达性，通过活动间的关系对系统出现问题的时候进行优化.文献[3]给出了在门禁系统工作时，如何针对异常情况进行问题解决的方法建议.文献[4]提出了在满足门禁系统运行环境正确的情况下，如何规划避免错误行为的问题想法.文献[5]给出了在业务流程建模时，将一个综合模型和结构树通过挖掘其中的模块，将其变化域与责任模型相结合来分析.文献[6]介绍了一种在Petri网中进行可达性检查的技术，利用组合性来提高一些众所周知的例子的性能.文献[7]给出了一个在存在内部连通网络的情况下，如何设计门禁运行系统的想法.文献[8]提出了一种诊断过程模型之间行为差异的技术.给定两个过程模型，它确定它们是否在行为上是等价的，如果没有，它会描述它们在行为关系方面的差异:如因果依赖或冲突,在一个模型中而不在另一个模型中.该方法作为原型实现，在业务流程模型和BPMN中作为输入流程模型，并以自然语言生成差异语句.

本文以基于Petri网的公寓门禁运行流程为例，建立源使用流程模型.同时以Petri网的基本定义与相关概念为基础，对源模型进行优化，实现用户方便快捷开启门禁的同时，能够最大化地保障用户安全的相关问题.

本文的第二节介绍Petri网相关概念；第三节建立公寓门禁运行流程模型并通过分析源模型中活动间的交互关系以及存在的问题对该模型进行优化；第四部分模型正确性分析和验证；第五部分总结全文，展望未来工作.

2 基本概念

定义1（流程模型Petri网）[1]一个流程模型Petri网PN=(P,T,F,C)是一个四元组，满足以下条件：

（1）P是有限库所集，T是有限变迁集；

（2）P≠Ø，T≠Ø 且 P∩T=Ø；

（3）F=(P×T)∪(T×P)表示 PN 的流关系且(P∪T,F)是强连通图；

(4)dom(F)∪cod(F)=P∪T 其中

dom(F)={x∈P∪T|∃y∈P∪T,(x,y∈F)}；

cod(F)={x∈P∪T|∃y∈P∪T,(y,x)∈F}.

（5）C={ang,xor,or}是流程网的结构类型.

我们用X=P∪T表示所有的节点，用F+表示流关系F的不自反传递闭包.对x∈X,*x={y|y∈P∪T∧(y,x)∈F}表示 x 的前集，x*={y|y∈P∪T∧(x,y)∈F}表示x的后集.

定义2（变迁发生规则）[2]一个四元组PN=(P,T;F,M0)称作Petri网，当且仅当：

（1）N=(P,T,F)为一个网；

（2）M:P→Z*为标识（或状态）函数，M0对于变迁是初始标识；

（3）变迁发生规则：

1）变迁t∈T可以发生，当且仅当对∀s∈*t:M(s)≥1，记作 M[t＞；

2）在标识M下使能的变迁t发生后，得到一个新的标识M'（记为M[t＞M')），则有，

定义3(可达性)[6]设PN=(P,T;F,M)是一个流程模型 Petri网.如果存在 t∈T，M[t＞M'，则称 M'为从M 直接可达.如果存在变迁序列 σ=＜t1,…,tn＞,n∈N和标识序列M1,…,Mn∈M使得

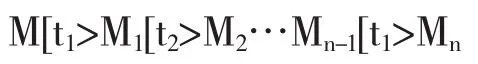
则称Mn为从M可达的.从M可达的一切标识的集合记为R(M).约定M∈R(M).

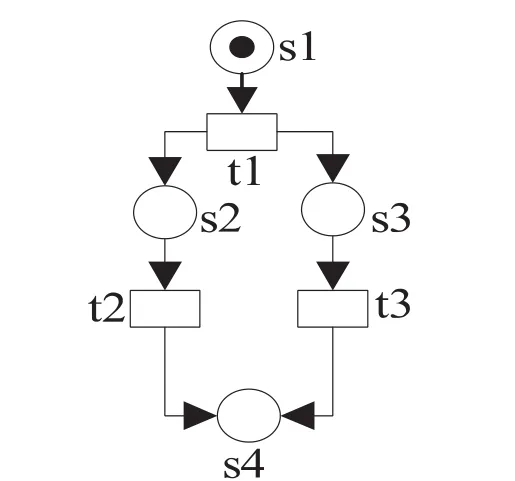
图1

如图1基于Petri网可达性建立模型，记M0[1,0,0,0],M1[0,1,1,0],M2[0,0,0,1]在初始状态M0下，变迁 t1，t2，t3都是使能的，即 M0[t1＞M1[t2,t3[M2.

定义4[1]（行为轮廓）设(N,M0)是一个网，初始标识为M0.对任给的变迁对(t1,t2)∈(T×T)满足下面关系;

（1）若 t1≻t2且 t2≯t1，则称严格序关系，记作t1→t2；

（2）若 t1≯t2且 t2≻t1，则称严格逆序关系，记作t1→-1t2；

（3）若 t1≯t2且 t2≯t1，则称排他关系，记作 t1∥t2；

（4）若 t1≻t2且 t2≻t1，则称交叉序关系，记作t1×t2；

（5）所有关系的集合叫作网系统的行为轮廓，记作

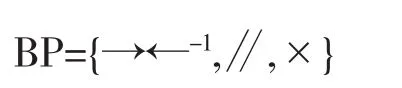
3 基于Petri网的门禁运行流程建模优化分析

本部分首先基于Petri网建立源使用流程模型，其次分析源模型中所存在的问题，进而通过对该模型增加库所或变迁的方式进行模型优化，使其具有适用性和有效性.

本文通过介绍门禁系统运行流程，介绍并说明了Petri网建模的优化性.在实际生活中，门禁系统应用于多个生活场景，例如：大学校园宿舍楼都安装了门禁系统，以控制非正常学生进出公寓，也预防了一部分的安全隐患问题.然而，实际的门禁运行流程存在诸多不完善的地方.如图2所示为门禁运行流程源模型图.

图2 门禁运行流程源模型图

表1 图2变迁符号的含义

用户准备进入公寓，在门禁系统上刷入住卡片，门禁系统识别卡片信息后上传至后台数据库并与数据库内用户信息进行匹配，若与数据库内信息相匹配，则系统认定为此公寓住户，并反馈开启门禁的指令至系统，随后系统便打开门禁，住户即可进入公寓.若上传信息与数据库内用户信息不匹配，则系统认定为非此公寓住户，并反馈错误信息，禁止系统打开门禁，刷卡者无法进入公寓.图2所示模型基本能够实现完整的门禁运行流程，但是存在如下一些问题:门禁使用方法局限、运行方式单一、开关闭系统不完善等问题.同时对于一些限定时间进入的公寓系统此模型并不太适用.例如某公寓限定晚十一点之前可通过门禁进入，即过了晚上十一点，即使刷卡信息正确，但是门禁系统仍不打开.我们针对如上问题对模型进行优化，如图3.

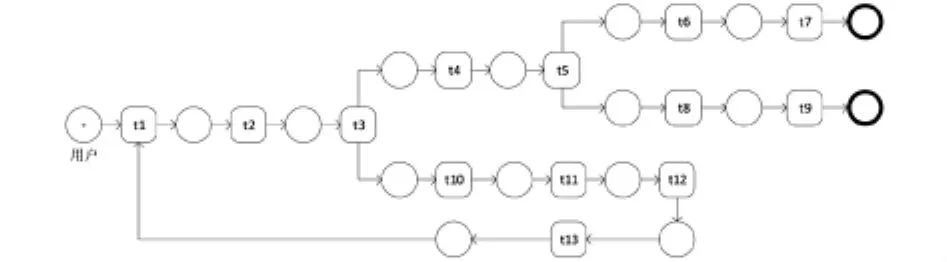
图3 门禁流程模型优化图

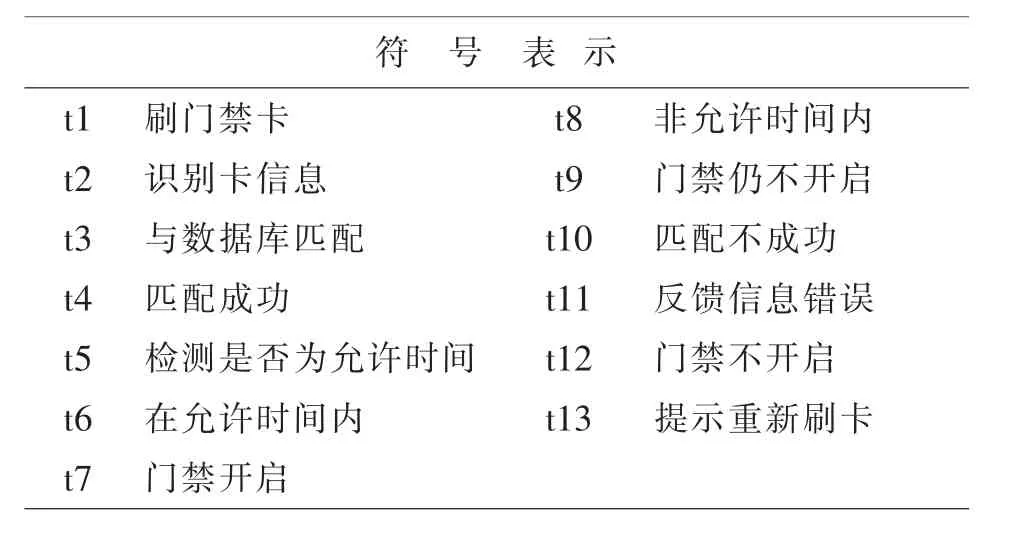
表2 图3变迁符号的含义

图3为门禁系统运行流程模型优化图，针对图1所出现的问题进行模型优化.在该模型中，存在允许通过时间段的情况下，在允许门禁开启的时间范围内，通过刷取正确信息的门禁卡，即可打开门禁，住户即可进入公寓.解决了开关闭系统不完善，运行方式单一的问题；同时在非允许开启门禁的时间段内，若刷取了正确的门禁卡，系统仍然不开启门禁.同时为了避免正确住户刷错了门禁卡需要重新刷取正确门禁卡的情况，也进行了模型的优化.通过让住户重新刷取正确门禁卡即可打开门禁系统，使得住户进入公寓，这解决了门禁使用方法局限的问题.

4 模型正确性分析和验证

本文第三部分详细介绍了在门禁运行使用流程中，存在如下问题：使用方法局限、运行方式单一、开关闭系统不完善等问题；当存在限定时间范围时，门禁系统运行处理各类问题情况等.图3门禁系统运行流程模型优化图针对如上问题进行了解决.

与图2相比，图3增加了s1=t5(t6+t7)+t5(t8+t9)这一变迁序列,帮助解决了限定时间范围内门禁系统通过与否的情况.同时s2=t3t10t11t12t13t1变迁序列改善了住户刷错门禁卡的情况，通过重新刷取正确的门禁卡来进入公寓.通过增加上述控制环节，使得源模型得到有效地优化.

5 结束语

本文基于Petri网构建的门禁系统运行模型给出了门禁运行系统优化模型，通过分析原有模型在系统运行中存在的不足，通过增加库所和变迁的方式对其进行优化.解决了用户在实际生活中使用门禁系统出现的运行方式单一，使用方法局限，门禁开关闭系统不完善等一系列问题.

本文基于Petri网所建立的优化模型也有一定的局限性.比如在非允许开启门禁时间段中，正确住户想进入公寓的情况，针对这一问题，没有给出具体说明及解决办法.未来我们将针对这些问题来一一进行解决.