五种类型不定积分问题的求解

唐梦鑫，朱 华

（攀枝花学院，四川 攀枝花 617000）

1 引言

微积分学的创立极大地推动了数学的发展.过去很多用初等数学无法解决的问题,运用微积分,问题往往迎刃而解,显示出微积分学的非凡威力.不定积分在微积分中占有至关重要的地位,而不定积分的计算对于大多数初学者来说是一个难点,笔者结合自身所学和实际所遇到的问题,将不定积分求解问题归为五种类型,并举例加以说明.

2 基本定义及性质

2.1 若在某个区间I上,函数F（X）和f(x)满足以下关系

则称F(x)是f(x)在这个区间I上的一个原函数.

2.2 函数f(x)的原函数全体称为这个函数的不定积分,记作

3 五种类型的不定积分

3.1 简单函数不定积分

直接用积分公式或者运算性质求解不定积分,或者将被积函数经过恒等变形 (三角变形,代数变形),代换(三角代换,整体代换,倒代换)后再利用积分公式或者运算性质求解.

例1计算

解

3.2 有理函数不定积分

由代数学基本定理可知:每个次数≥1的有理系数多项式都能唯一的分解成不可约的有理系数多项式的乘积.在求复杂的有理函数不定积分时,可将复杂的不定积分分解成简单的不定积分后再求解.

例2计算

解根据代数基本定理可将x2+3x-10分解成(x-2)(x+5)的形式.

解得:A=B=1.

3.3 无理函数不定积分

例3计算

解令,则有

由于

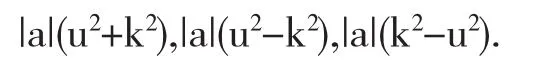
因此上述无理根式的不定积分也就转化为以下三种类型之一:

当分别令 u=ktant，u=ksect，u=ksint后, 它们都转化为三角有理式的不定积分.

例4

解被积函数的存在域为-∞＜x＜+∞,因此,令x=atant,并限制.从而

代入得

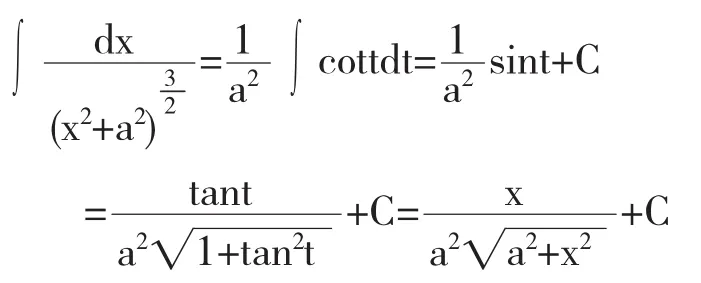
3.4 三角函数不定积分

对于三角函数不定积分的求解,最通用的方法就是万能公式法,但由于万能公式过于复杂,所以除非万不得已一般不采用万能公式.最常用的方法就是将其通过诱导公式恒等变形,再利用换元法,积分法进行求解.

例5计算

解

3.5 超越函数的不定积分

所谓的超越函数就是指:将三角函数,反三角函数,对数函数,指数函数等初等函数中的一个或多个函数混合成一个函数.在解超越函数不定积分时最基本的方法就是分部积分法,将一个超越函数不定积分分解成多个不定积分分别求解,再利用不定积分的线性性质求和.

例6计算

解

4 总结

观察对比以上五种类型的不定积分,我们可以发现它们都有共同点:无论是何种类型的不定积分,做何种变换,其目的都是将繁琐的不定积分等价转化成最简单的不定积分,再套用公式求解.