混合指数分布的矩估计

王秋爽，徐圣楠

（吉林师范大学 数学学院，吉林 四平 136000）

1 引言

混合指数分布是寿命分析中的重要统计模型.混合指数分布模型，广泛应用于生存分析、生物医学统计、故障诊断、金融、可靠性分析等领域，受到统计学家和实际工作者的广泛研究.关于混合指数模型国内外已有很多研究，如Mc-Clean针对分组数据的混合指数分布的参数进行估计.Jones等研究了截尾数据下混合指数分布的贝叶斯估计.朱利平等基于EM算法讨论了完全数据和截尾数据下混合指数模型的参数估计.赵亚林对单参数混合指数分布的参数估计方法进行了相关探讨.田玉柱等基于EM算法，利用极大似然估计方法，对混合删失样本下的参数进行估计.韩静针对利用EM算法进行参数估计的缺陷，提出了采用退火遗传算法（SAGA）对双参数混合指数分布模型的参数进行优化估计.雷庆祝等利用贝叶斯（EB）估计,研究强混合样本下刻度指数分布族的参数.经过对上述文献的研究，得出如下结论：EM算法虽然可以对混合分布在正常工作条件下的参数进行估计，却可能会收敛到局部最优值.针对混合分布的参数估计，直接利用极大似然估计方法进行研究，在求最大似然估计量时，往往要解一个似然方程（方程组），计算量较大，同时结果又不是很理想，有的时候比较难解，甚至根本就解不出有限形式的解.退火遗传算法容易过早收敛，产生早熟现象.为了克服以上算法的不足之处，寻求一种新的估计方法来实现混合指数分布模型参数的最优估计显得尤为重要.

矩估计作为常见的参数估计方法，其思想是利用样本矩去替换相应的总体矩.只要总体相应的矩存在，矩估计方法对任何总体都可以进行估计，并且不需要知道总体具体分布的数学形式.部分文献已经开始尝试利用矩估计法来估计混合分布的参数：如尹剑等研究了二元极值分布混合模型的矩估计及渐近方差，并将其与极大似然估计的渐近方差进行比较,结果表明，矩估计是一个较好的估计.李建丽等研究了混合几何分布的矩估计.矩估计作为重要的估计方法，利用矩估计来研究混合指数分布参数的文献却并不多见，鉴于此，本文基于矩估计方法，对混合指数分布进行参数研究，极大地简化了计算过程.

2 混合指数分布的矩

设随机变量X服从如下概率密度函数

其中，λ1＞0，i=1,2 是未知参数，α∈(0,1)表示第 1 个成分在该混合分布中的比重，此概率密度函数是两个指数分布的加权平均，本文即对该分布进行研究.

定理1设X服从概率密度函数为式（1）的混合指数分布，则有：

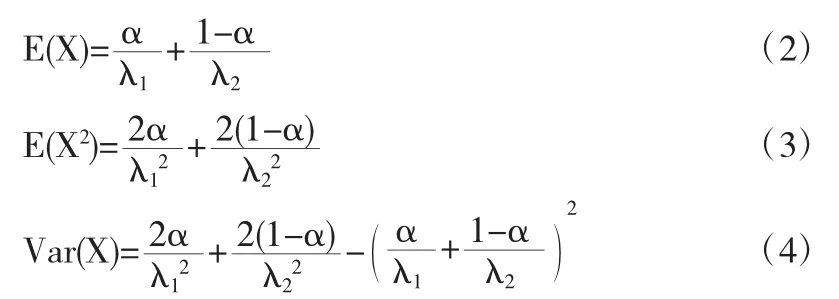
证明设X～Exp(λ)，可知指数分布的期望、二阶矩，E，根据 Var(X)=E(X2)-(E(X))2，利用期望、方差的性质10可得混合指数分布的期望、二阶矩、方差为：

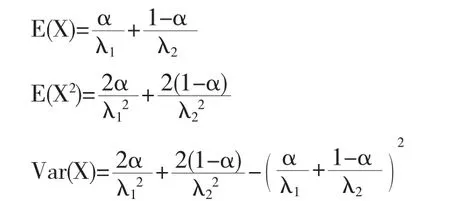
定理2设X服从参数为λ的混合指数分布，则X的k阶矩为：

证明利用数学归纳法证明11.

假设对于k-1(k≥2,k∈Z)定理成立，即

E(Xk-1)=，则：X的k阶原点矩：

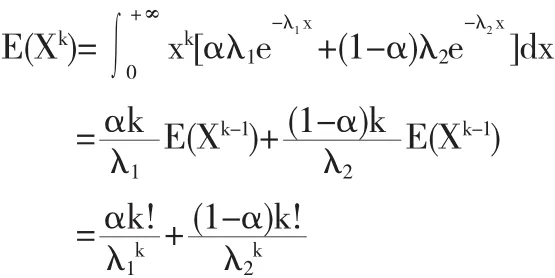
由此，可得混合指数分布的多阶矩为：

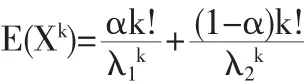
3 混合分布的矩估计

3.1 具有一个未知参数

定理 3若 λ1和 λ2已知，α 的矩估计为且是α的无偏估计.

证明用替换式（2）中的 E(X)，则有

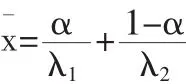
定理 4若 α 和 λ1已知，λ2的矩估计为

定理5若 α 和 λ2已知，λ1的矩估计为

定理3和定理4的证明方法，同定理2，此处省略.

3.2 具有两个未知参数

定理6如果λ1已知，参数α、λ2的矩估计分别为：

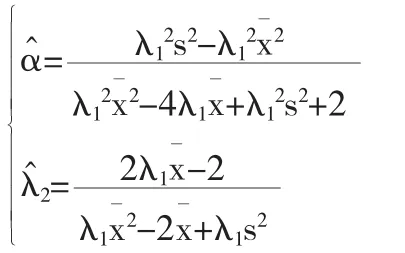
证明用分别替换（2）、（4）中的 E(X)、Var(X)，联立方程组：

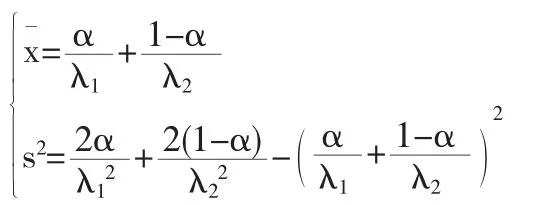
借助MATLAB软件，求解该方程组，解得α、λ2的矩估计分别为：

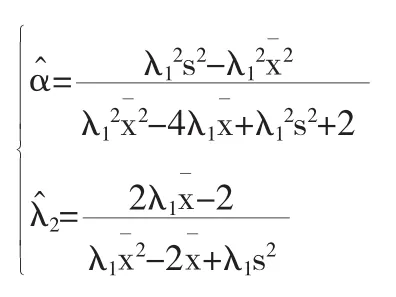
定理7如果λ2已知，参数α、λ1的矩估计分别为：

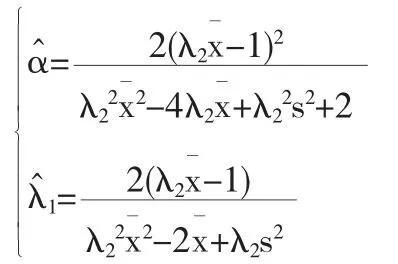
证明过程同定理6，此处省略.

3.3 具有三个未知参数

当α、λ1、λ2三个参数均未知时，可以将样本均值、样本方差、样本多阶矩分别替换定理1中对应的期望、方差、二阶矩，定理2中的多阶矩来进行估计，经过尝试发现，将联立的方程进行直接求解并不容易，很难得出可行解，建议在三个参数均未知时，多种方法结合求未知参数.

4 总结

本文构造了混合指数分布这一数学模型，利用矩估计法，首先对混合指数分布的均值、方差、多阶矩进行求解，再利用这些结果建立参数估计方程（方程组），在计算具有一个未知参数的混合指数模型时，利用概率论的基础知识，进行了详细的推导，并针对估计出的参数进行了无偏性检验，验证了参数的有效性.在两个参数未知的情况下，联立方程组对未知参数进行估计，并借助MATLAB软件求解，省去了繁琐的求解过程.该方法既可以弥补传统优化模型容易陷入局部最优解的局限性，又可以改善退火遗传算法容易早熟的不足之处.文章中提出的方法具有普遍的适用性，适用于各种仪器、电工电子元件的可靠性寿命分布的参数估计.