不同筋材刚度下加筋土挡墙离心模型试验

， ，,

(华中科技大学 土木工程与力学学院，武汉 430074)

1 研究背景

加筋土挡墙作为一种新型挡土结构，与传统挡土墙相比，具有力学性能优、造价低、地形适应性好等优点。随着加筋土技术发展和推广，其逐渐广泛应用到公路、桥台、堤坝等工程领域。世界各国也相应地编制了各种加筋土挡墙设计规范和指南，但这些规范指南总体上偏于保守[1-2]。为了简化设计计算，规范[3-9]都基于极限平衡法和土压力理论，没有考虑筋-土相互作用，更没有说明正常服役状态下筋材内力如何计算，不能反映非极限状态下加筋土挡墙结构内力的真实分布情况。

为了研究加筋土挡墙中筋材内力如何分布，常常借助于大型现场试验和土工离心试验，而目前加筋土结构离心模型试验的难点，在于模型筋材的选取与筋材应变的测量。常规方法是直接在筋材上贴应变片。由于离心模型试验根据加速度对原型要进行缩尺，至少缩小20倍以上，但常规土工格栅单根肋宽都不超过3 cm，严格进行缩尺后肋宽不足1.5 mm，格栅的整体外形几乎跟窗纱一样，造成了贴应变片测量的困难，同时应变片的胶黏剂又会造成“窗纱”局部刚度过大。对于上述难题，国内外大量学者对格栅应变的测量方法进行了大量探索。

Sharma等[10-11]、俞松波等[12]针对加筋土挡墙离心模型试验中筋材应变难以准确测量的情况，提出了在模型格栅浇筑环氧树脂带，通过应变片测环氧树脂变形来间接获得模型格栅受力情况。

Raisinghani等[13]在加筋边坡离心模型试验中，通过在筋材横肋端部连接彩色塑料标记点，利用数字图像技术观测标记点的位移来间接计算筋材的真实应变。

基于上述测量方法，国内外学者做了大量加筋土结构离心模型试验。徐超等[14]通过圬工与加筋土组合式挡墙离心模型试验论证了间接加筋作用及密筋状态下加筋土挡墙的工作机理。Costa等[15]采用无纺布加筋土挡墙，对比某个加速度下长期加载和该加速度下短期加载下的性能，研究加筋土挡墙性能与时间的相关性。朱海龙等[16]采用不同拉伸强度和不同网格尺寸的网格式材料作为加筋材料，对加筋土挡墙离心模型的破坏形式进行了研究。Balakrishnan等[17]对反包式加筋土挡墙采用不同刚度筋材进行离心试验研究其工作性状。

本文采用自制的高密度聚乙烯(HDPE)格栅，筋材应变测量方法则在常规方法的基础上做了一定的取舍和调整，对不同筋材刚度的砌块式加筋土挡墙进行了2组土工离心试验，研究了试验过程中土工格栅应变、面板水平位移及土压力分布情况。

2 加筋土挡墙离心模型试验

2.1 试验设备

本次试验采用长江科学院CKY-200土工离心机，其有效容量200g-t；最大加速度200g；有效半径3.7 m；模型箱内部尺寸为100 cm(长)×40 cm(宽)×80 cm(高)。

图1 CKY-200土工离心机Fig.1 CKY-200 geotechnical centrifuge

2.2 试验方案概况

设计了2组不同格栅刚度的加筋土挡墙离心模拟试验，模型缩尺比例1∶20，2组试验对应的离心机试验模型参数如表1所示。

表1 试验模型参数Table 1 Parameters of test model

2.2.1 试验土样

试验土样采用粉砂，其级配如图2所示。测得的平均含水率为1.04%，最小干密度为1.09 g/cm3，最大干密度为1.58 g/cm3。对该土样分别进行了100，200，400 kPa围压下的三轴固结排水试验，测得黏聚力cd=0，内摩擦角φd=37.5°(见图3)。

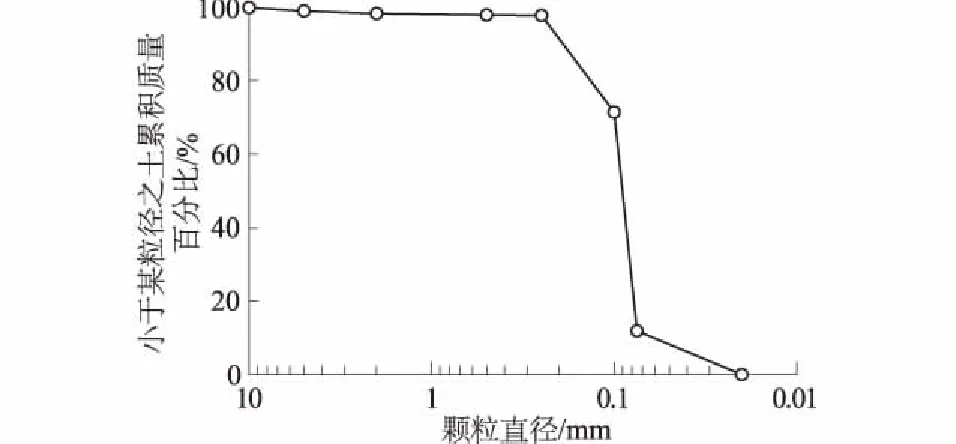
图2 砂土的级配曲线Fig.2 Grain size distribution curve of sand soil

图3 砂土的强度包络线Fig.3 Strength envelope of sand soil

2.2.2 试验模型筋材

采用HDPE土工膜自制而成的土工格栅，其厚度为1.0 mm，平面尺寸分别如图4所示。为了能够在格栅纵肋上贴应变片，纵肋宽度设计为5 mm，并没有严格按照比例进行缩尺，2种格栅进行拉伸试验，拉伸速率为0.2%/min，其拉应力-应变关系如图5所示。T1格栅和T2格栅应变2%的割线刚度分别为88.9，57.2 kN/m。

图4 格栅局部尺寸Fig.4 Local dimensions of geogrid

图5 T1和T2格栅应力-应变曲线Fig.5 Stress-strain curves of geogrids T1 and T2

2.2.3 挡土墙模型面板

采用铝合金加工而成砌块式面板，相邻砌块之间通过直径1.8 mm钢丝连接。砌块弹性模量为7×104MPa，密度为2.81 g/cm3，尺寸为10 mm(宽)× 15 mm(高)。

2.2.4 模型箱

为了反映加筋土挡墙平面应变情况，应尽量减小模型箱两侧壁与模型之间的摩擦，为此本试验在侧壁粘贴双层聚四氟乙烯(Teflon)薄膜，如图6所示，并在2层薄膜之间涂抹润滑油。

图6 模型箱侧壁上聚四氟乙烯薄膜Fig.6 Teflon film on the lateral face of model box

2.2.5 加筋土挡墙模型装配

模型尺寸如图7所示，首先进行地基的制备，地基土分3层填筑，每层5 cm高，采用人工静力压实，控制其密度为1.44 g/cm3，相对密度Dr=0.784；地基制备完成后，先用木板做成加筋土挡墙的水平支护，然后每安装一层挡土墙面板，就进行一层填土压实，填土密度控制在1.42 g/cm3，相对密度Dr=0.749，每两层面板后部安装一层土工格栅，格栅长度为20.5 cm，竖向间距3 cm，依次往复直至填筑达到设计图中高度30 cm；最后为防止模型在吊装过程中受到扰动，必须等放入离心机吊篮后，方可拆除水平支护。

图7 加筋土挡墙模型示意图Fig.7 Sketch of reinforced soil retaining wall model

2.3 试验监测及布置

2.3.1 试验监测装置

本次试验监测项目为:筋材应变、面板水平位移、加筋土挡墙顶部填土竖向沉降、挡土墙面板后方及潜在滑动面处的竖向土压力，该潜在滑动面是根据文献[8]和文献[9]假定的。其监测装置采用离心机专用的精密传感器：位移计分别为量程30～80 mm和40～160 mm的激光位移计，其测量精度为0.01 mm。型号SAK120-1-C11-P003M- V2M应变片用于测量应变，为降低离心机运转过程中的电子信号干扰，应变片采用了半桥连接。土压力盒为降低尺寸及重量对被监测模型内部应力场的影响，采用了中国工程物理研究院总体工程研究所生产的微型土压力盒，尺寸10 mm(直径)×2 mm(厚度)，量程分别是500，200 kPa。

图8 传感器布置示意图Fig.8 Arrangement of sensors

2.3.2 试验监测装置的安装布置

土工离心试验模型监测点的布置如图8所示。

(1)土压力盒：在面板上布置2组土压力盒(EV1和EV4)分别测量墙高H=45，165 mm处面板后部的竖直土压力；在规范中的潜在破坏面处布置3组土压力盒(EV2，EV3，EV5)分别测量H=45，105，165 mm潜在破坏面处的竖直土压力。

(2)激光位移计：H=67.5，157.5，232.5 mm布置3个激光位移计(LDS1，LDS2，LDS3)测量面板水平位移。

(3)应变片：在10层土工格栅中选取其中5层——第1、第2、第4、第6、第8层，对应的墙高分别为15，45，105，165，225 mm，并且在这5层格栅的中间纵肋上均匀布置4个应变片(如图9所示)，共计20个应变片。

图9 土工格栅上的应变片Fig.9 Strain gauges on the geogrid

本试验应变片贴法与常规方法有所区别，其步骤如下：先砂纸打磨并酒精清洁，再用百得(Pattex)PSK6C胶水将应变片粘在格栅上，并用Teflon膜摁压应变片约2 min直至胶干，Teflon膜作为保护层保留在应变片上，再用绝缘胶布覆盖。采用Teflon做保护层，而不用硅胶，这是因为Teflon非常光滑，对应变片变形几乎没有影响。

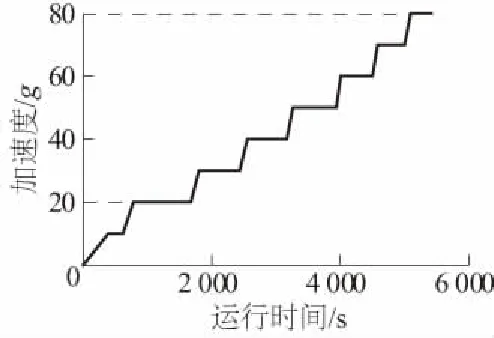
图10 离心试验加载过程Fig.10 Loading process of centrifugal test

2.4 试验加载过程

试验加速度从0加载

到80g(如图10)，每加载10g稳定5～10 min进行监测记录，然后继续加载。本次土工离心试验缩尺比例1/20，故在20g时进行较长时间约15 min的监测。

3 试验结果

2组不同筋材刚度的加筋土挡墙模型在土工离心机加速度从0加载到80g过程中均没有出现破坏。在离心机停止运行后从2组模型均观测到，在顶部加筋区与非加筋区交界处(距离面板背面约20 cm)的填土出现了平行于面板的微裂纹带(图11(a))，而且在距离面板后部约1 cm处也出现了平行于面板的微裂纹带(图11(b))。试验完成将逐层挖开的过程中发现加筋区中靠近面板区域(距离面板0～8 cm)出现凹陷，由于模型箱侧壁的摩擦效应，使得中部填土沉降大于模型箱侧壁处填土沉降(图12)。

图11 顶部填土出现裂纹Fig.11 Cracks on the crest backfill soil

图13 T1和T2筋材最大应变随墙高分布Fig.13 Distribution of peak strain for reinforcements T1 and T2 versus elevation

3.1 筋材应变

从筋材最大应变随墙高分布(图13)可以看出，应变沿面板高度呈不均匀分布，顶部筋材应变最小，顶部向底部逐渐增大，最大应变出现在加筋土挡墙中下部，在最底部突然减小，这与文献[18]和文献[19]中现场试验监测统计结果非常相似。同时低刚度筋材变形均大于相同加速度下相应位置高刚度筋材的变形。其中最底部(靠近地基区域)筋材应变突然减小，这是由于底部砌块与地基之间的摩阻力限制了底部面板的位移，底部面板位移受限致使该区域土体侧向变形受到约束，由筋土变形协调理论[20-21]可推知筋材应变也将会减小。

T1，T2筋材应变的水平分布分别如图14和图15所示。

图14 T1筋材应变水平分布Fig.14 Horizontal distribution of strain of reinforcement T1

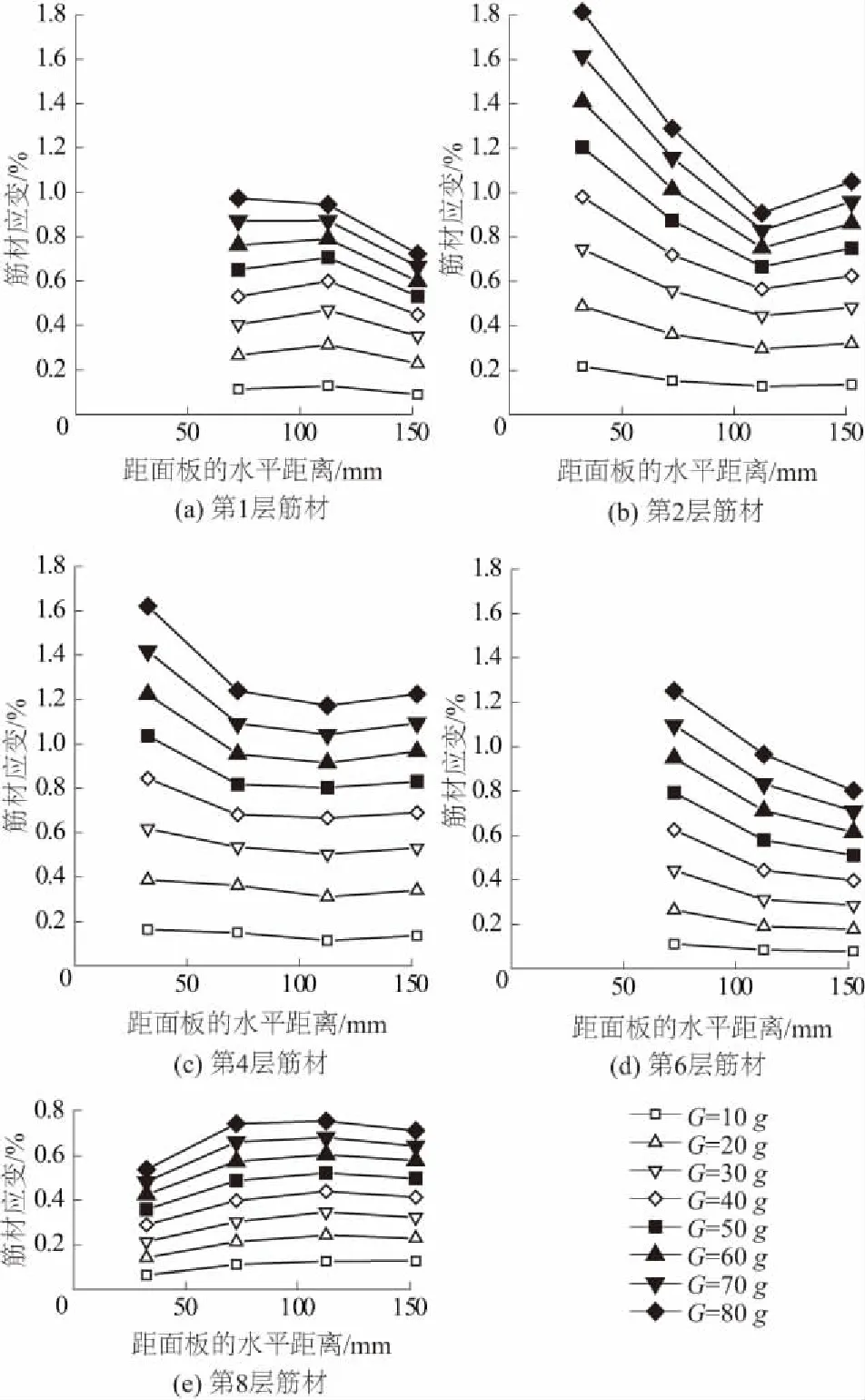
图15 T2筋材应变水平分布Fig.15 Horizontal distribution of strain of reinforcement T2

图14、图15中筋材应变的水平分布表明，在低重力场下(10g至20g)筋材应变沿水平方向呈均匀分布，并且随加速度增加逐渐出现不均匀分布；而在高重力场时(50g及以上)处于潜在破坏面(由图8虚线标示)附近监测点筋材应变值明显大于同高度的其他位置，在该点出现峰值。同时对比T1，T2筋材可以看出随加速度增大，T2筋材更早出现峰值点，而且T1筋材仅中下部的几层筋材应变才出现峰值，其他层基本呈均匀分布，说明相同重力下加筋土挡墙筋材刚度越小，越容易发挥筋材应变，也越早形成潜在滑动面。

图16 不同加速度下各监测点的竖向土压力分布Fig.16 Distribution of vertical earth pressure of monitoring points under different accelerations

3.2 竖向土压力

由于文章篇幅有限，且各监测点的竖向土压力值随加速度增大而均匀增大，规律性很强，这里仅列举了重力场20g、80g的竖向土压力分布(如图16所示)。竖向土压力沿墙高分布与土自重应力分布趋势一样——顶部到底部逐渐增大，顶部最小、底部最大。当加速度相同时，潜在滑动面附近的监测点土压力显然大于相同高度面板区域的竖向土压力，且潜在滑动面处测得土压力接近竖向土压力理论值，而面板处测量值远小于理论值。对于上述现象，笔者认为：第一，在面板区域面板对填土产生竖直向上摩阻力，削弱了竖直向下的填土自重应力的作用；第二，从图12可以看出，面板区域填土沉降形成了凹陷区，该凹陷区使得格栅类似网兜一样分担了一部分填土竖向应力，并间接传递给面板，最终使得向下传递的竖向土压力变小。

图16中不同筋材刚度情况下，位于潜在滑动面处竖向土压力基本相同，可以看出筋材刚度的不同对竖向土压力分布及大小几乎没有影响。

结合图16各监测点的土压力分布与图14(c)、15(c)中第4层筋材应变水平分布可以看出，靠近面板处应变片并非位于潜在滑动面区域，且该处土压力远小于潜在滑动面土压力，但筋材应变又远大于潜在滑动面处应变，说明靠近面板的筋材应变不能简单地用土压力理论来解释，还应考虑不均匀沉降引起的面板与加筋土间的拉拽作用等其他因素。

3.3 面板水平位移

图17 H=232.5 mm处面板水平位移Fig.17 Horizontaldisplacement of facing when H=232.5 mm

图17中表示了重力场20g到80g过程中T1，T2筋材上部面板监测点(墙高H=232.5 mm)的水平位移，可以看出：水平位移随加速度均匀增大；当采用筋材刚度不同时，加速度较小时面板顶部位移基本相同，但加速度70g以上时才开始出现差异。 对于上述现象解释是：受到相同重力时，低刚度筋材要产生更大的变形才能满足筋、土、面板受力平衡，这一点从图13中TI，T2筋材应变的对比可以看出，但图14(e)、15(e)中顶部筋材应变非常小，顶部筋材应变没有完全发挥出来，再加上面板与面板之间的约束作用、地基对面板整体的约束作用，因而顶部面板水平位移非常近。

4 结 论

(1)整体来看，当采用低刚度筋材时，筋材的变形更加显著，但不同筋材刚度对竖向土压力的分布及大小基本没有影响。

(2)对于面板竖直的加筋土挡墙，其筋材最大应变发生在面板中下部，该分布趋势与文献[18]和文献[19]现场试验及统计的结果非常相似。筋材沿水平方向的变形分布，在低重力场时基本均匀分布，但重力场较大时出现明显的不均匀分布，而峰值点基本位于规范中潜在滑动面附近。

(3)潜在滑动面处竖向土压力测量值很接近填土自重应力理论值，面板处竖向土压力测量值明显小于理论值，而在中下部面板连接区域筋材应变也出现了峰值，说明面板处筋材应变不能简单地用传统的土压力理论来解释，还应考虑不均匀沉降引起的面板与加筋土间的拉拽作用等其他因素。