纯电动拖拉机机电耦合系统非线性振动分析
严国军, 杨 彦, 顾建华, 姚月琴,祁 淼,4
(1. 盐城工业职业技术学院 机电工程学院,江苏 盐城 224000; 2. 东南大学 机械工程学院,江苏 南京 210000; 3. 南京理工大学 控制工程学院,江苏 南京 210000;4. 江苏大学 汽车工程学院,江苏 镇江 212000)
0 引 言
在我国,电动农业机械还处于研究阶段。无论从市场需求,还是能源发展方向等方面考虑,电动农业机械都是我国新农村建设和现代农业发展的需要。我国“十二五”规划曾明确提出:“提高设施装备水平,提升产业发展质量,促进设施农业可持续发展”。随着新能源车辆的发展,作为农业大国,纯电动拖拉机正在慢慢替代传统燃油拖拉机,并且应用在农业的各个方面。
纯电动车辆动力传动系统中普遍存在机电耦合现象,研究机电系统耦合振动,可减小系统非线性特性的影响。纯电动车辆动力传动系统的扭转振动问题在电磁激励和外部激励的作用下变得复杂与突出。在机电耦合方面,林利红等人对纯电动车辆动力传动系统进行机电耦合动力学分析和实验研究,建立了系统的机电耦合振动仿真模型,仿真分析了由于电流调节器参数、阻尼、谐波扰动、间隙以及负载扰动等因素引起的机电耦合振动动态过程,并将物理实验研究与理论分析结果进行对比和验证[1]。在车用电机非线性扭转振动方面,陈星等人采用多尺度法研究了纯电动车辆动力传动系统的扭转振动系统特性,仿真结果表明合理的设计和控制电机的电磁参数和机械参数,可以解决电机扭振系统出现的跳跃分岔等非线性特性现象[2-3]。
针对低速重载起步工况下纯电动拖拉机机电耦合传动系统受到非周期冲击干扰力作用,分析扭转角与电磁转矩的耦合影响。为此笔者通过建立纯电动拖拉机机电耦合传动系统的非线性扭转振动模型,求解无扰动Hamilton系统的平衡点;利用Melnikov法求解分岔阈值曲线,分析电机控制参数对纯电动拖拉机机电耦合传动系统非线性动力学行为的影响;基于Melnikov理论分析研究传动系统的分岔和混沌特性,从而求解系统稳定性运行边界条件。
1 机电耦合扭转振动模型
1.1 电机模型的建立
不同情况下,永磁同步电机的稳定运行时的相量如图1。

图1 永磁同步电机相量Fig. 1 Phasor diagram of permanent magnet synchronous motor

由图1得到如下关系式:
(1)
通过求解式(1)可得到电机定子电流的直、交轴分量:
(2)
定子相电流:
(3)
而电机的输入功率:
P1=mUI1cosφ
(4)
当忽略定子电阻,由式(4)可得到电机的电磁功率:
(5)
则电机的电磁转矩:
(6)
式中:m为电机相数;Ω为机械角速度,且ω=pΩ,其中,ω为电机的电角速度,p为电机的极对数;E0为空载反电动势,可由式(7)计算得到。
(7)
式中:f为电源频率;Kdp为基波绕组系数;N为每相串联匝数;Φ10为永磁体基波磁通;Am为永磁体面积;Br为永磁体剩磁;σ0为空载漏磁系数;bm0为永磁体空载工作点假设值;KΦ为气隙磁通波形系数;αi为计极弧系数;αp为极弧系数,δ为气隙长度,D为定子内径。

Te=b1sinθ+b2sin 2θ
(8)
由图1可知,θ=φ+ψ,因此可得到sinθ和sin 2θ三角函数展开式。
利用sinx≈x-1/6x3,cosx≈1-1/2x2,泰勒展开的近似式将含φ的三角函数展开并化简,即可得到作用于转子的电磁转矩:
Te=k0+k1φ-k2φ2-k3φ3
(9)
式中:k0=b1sinψ+b2cos 2ψ;k1=b1cosψ+2b2sinψ;k2=1/2b1sinψ+2b2sin 2ψ;k3=1/6b1cosψ+4/3b2cos 2ψ。
1.2 机电耦合扭转振动模型
通过分析车载永磁同步电机机电耦合扭转振动特性,将转子系统和传动系统进行简化,可以等效为二质体机电耦合转子模型[4-5],如图2。图中永磁同步电机转子与机械转子之间弹性联轴器联接,电机机座可视为刚性。图中Te是电磁转矩,TL是负载转矩。

图2 二质体机电耦合转子系统Fig. 2 Two plastid electromechanical coupled rotor system
根据牛顿定律,二质体转子系统扭转振动动力学方程为:
(10)

(11)
当转子系统处于稳态运行时,式(10)通过方程变换并消除得到公式中的静态项:
(12)
则机电耦合扭转振动动力学方程可转化为无量纲形式:
(13)
式中:v=J1/J2;r=1/(1+v);μ=(1/J1+1/J2)C;β=k2r2/J1;γ=k3r3/J1;η2=ω0-k1r/J1,ω0为不考虑机电耦合时转子系统的机械固有频率,可由式(14)进行计算:
(14)
从式(14)可看出,动力学方程具有平方项和立方项,方程为典型的非线性动力学方程。因此,考虑到机电耦合效应,传动系统转子扭转振动方程将有明显的非线性特征。
2 系统平衡点分析
选取的拖拉机电机额定功率为7.5 kW,额定电压为96 V,其他相关电机参数如表1。

表1 电机参数表Table 1 Motor parameter list

式中:ε为小参数,且0<ε≪1。
无扰动系统的势函数在研究非线性动力学行为中具有十分重要的作用,因此需要讨论无扰动系统的函数。当ε=0时,排除阻尼项和扰动项,函数方程变为无扰动系统:
(16)
在排除阻尼项和扰动项后,转子动力学系统为Hamilton系统,其Hamilton方程为:
(17)
式(17)对应的势函数为:
(18)
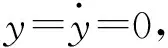
Hamilton系统平衡点稳定性分为如下几种情况:
1)情况A
当β2≤4γ(1-κ),Hamilton系统只有一个平衡点P0(0,0):
①情况A1:当κ<1时,P0是中心点。
②情况A2:当κ>1时,P0是鞍点。
2)情况B
当β2>4γ(1-κ)和4γ(1-κ)>0时,有3个平衡点,分别为P0(0,0),P1(x1,0),P2(x2,0):
①情况B1:当γ>0时,P1(x1,0)是鞍点,P0(0,0)和P2(x2,0)是中心点。当β=0.8,κ=0.35,γ=0.2时,可以得到势函数和相轨迹如图3(a)和图3(b),从图3(a)和图3(b)中可看出存在横截同宿轨道。
②情况B2:当γ<0时,P1(x1,0)是中心点,P0(0,0)和P2(x2,0)是鞍点。当β=0.8,κ=1.65,γ=-0.2时,可得到势函数和相轨迹如图3(c)和3图(d),从图3(c)和3图(d)中可以看出存在横截异宿轨道。
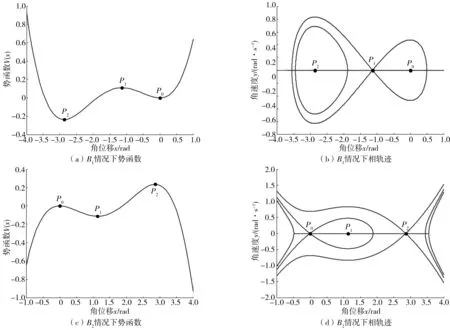
图3 B1和B2情况下Hamilton系统势函数和相轨迹Fig. 3 Potential functions and phase trajectories of Hamilton systems in the case of B1 and B2
3)情况C
当β2>4γ(1-κ)和4γ(1-κ)<0时,有3个平衡0点,分别为P0(0,0),P1(x1,0),P2(x2,0):
①情况C1:当γ>0时,P0(0,0)是鞍点,P1(x1,0)和P2(x2,0)是中心点。当β=0,κ=1.5,γ=0.2时,可得到势函数和相轨迹如图4(a)和图4(b),从图4(a)和图4(b)中可以看出存在横截同宿轨道。
②情况C2:当γ<0时,P0(0,0)是中心点,P1(x1,0)和P2(x2,0)是鞍点。当β=0.8,κ=1.65,γ=-0.2时,可得到势函数和相轨迹如图4(c)和图4(d),从图中可以看出存在横截异宿轨道。

图4 C1和C2情况下Hamilton系统势函数和相轨迹Fig. 4 Potential functions and phase trajectories of Hamilton systems in the case of C1 and C2
综合以上分析可知:情况A中只存在一个平衡点,将不做讨论;情况B和C均具有3个平衡点,而在情况B1和C1中,对较小的扰动幅值,Hamilton系统具有封闭轨道,此时将产生横截同宿轨道,可能导致同宿混沌;在情况B2和C2中,增加激励幅值,将会产生横截异宿轨道,可能导致异宿混沌。
从图3和图4中可以看出,考虑机电耦合作用的Hamilton系统是双势对称或不对称波动系统原型,同时由于机电耦合动力学方程系数的复杂多变,所以机电系统扭转振动将会表现出复杂的非线性动力学行为。车用永磁同步电机传动系统为获得更高的传动范围和高功率密度,通常设计和控制于弱磁效应,因此,笔者只讨论ψ>0的情况。当内功率因数角ψ在[0,π]内变化时,Hamilton系统的情况如图5。分析图可知,系统只存在B1和C1两种情况,笔者将以C1为例进行进一步讨论(B1可采用相似的过程进行计算讨论)。

图5 机电传动系统的平衡点的稳定性分类Fig. 5 Stability classification of the equilibrium points ofelectromechanical transmission system
已知例C1中,P0(0,0)是鞍点,P1(x1,0)和P2(x2,0)是中心点。系统Hamilton量为:
(19)
当H(0,0)=0时,存在两条连接鞍点(0,0)的同宿轨道{q0(t)}。同宿轨道求解过程如式(20):
(20)
由式(20)可得:
(21)
积分得:
(22)
当t=0,x0=±1时,c=0。整理后得两条同宿轨的参数方程为:
(23)
3 混沌阈值
当扰动项增加到Hamilton系统时,封闭的同宿轨将被破坏,此时可能会导致分岔,全局同宿分岔预示着混沌运动。Melnikov方法可以估算存在同宿分岔的参数空间,并可以转化为混沌,从而确定机电耦合扭转振动混沌运动的阈值[6-7]。因此,在分析同宿分岔时,将系统(15)写成状态方程的形式为:
(24)
Melnikov方法实际上是通过计算双曲不动点的稳定和不稳定流形之间的距离来确定系统是否存在横截同宿点。根据Smale-birkhoff同宿理论,当μ≠0,f≠0,且足够小时,系统(15)可能存在Smale马蹄存在意义下的混沌。根据Melinkov理论,Melnikov方程为:
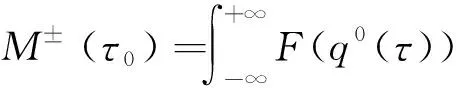
(25)
式中:q0(τ)=(x±,y±),代表Hamilton系统的同宿轨道;F∧G=f1g2-f2g1。
将式(24)代入式(25)中,初始条件为t=0,x0=±1,y0=0时,y±(τ)是时间τ的奇函数。则可得到:
(26)
式中,I1和I2分别为部分积分:

所以,对于一定频率,当满足式(27)时,系统可能产生Smale马蹄变换意义下的混沌。
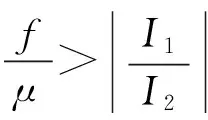
(27)
式(26)第一项积分I1可通过数学软件计算直接求得I1=0.372 7;第二项积分I2在求解过程相当复杂,所以采用数值积分法,通过采用数值积分法画出混沌阈值曲线,然后根据阈值曲线同样能够对系统做定性和定量分析。Melnikov函数数值积分法求解过程如下:
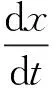
(28)

对式(28)分离变量,并对两边同时积分,得到:
(29)
将式(28)和式(29)代入I2中得到:
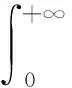
(30)
式(30)可以计算得到对应ω值的I2值,代入式(31)即可得出随ω变化的Melnikov阈值曲线。以f作为控制参数时,Melnikov阈值曲线如图6。在一定条件下,在f-ω平面上存在混沌区域。当f在该区域取值时,系统存在Smale马蹄变换意义下的混沌。

图6 同宿分岔的阈值曲线(μ=2.5)Fig. 6 Threshold curve of homoclinic bifurcation (μ=2.5)
4 数值计算分析
利用Runge-Kutta法对扰动系统(15)进行数值仿真,来进行验证上述用Melnikov方法做出的判断是否正确,从而对得到对应的时域波形、相轨迹、庞加莱截面图和幅值谱进行分析。图7为μ=2.5,ω=1.0,ε=0.1,时,F=εf,以f为控制参数时的系统分岔图,初始条件为x=0,y=0。
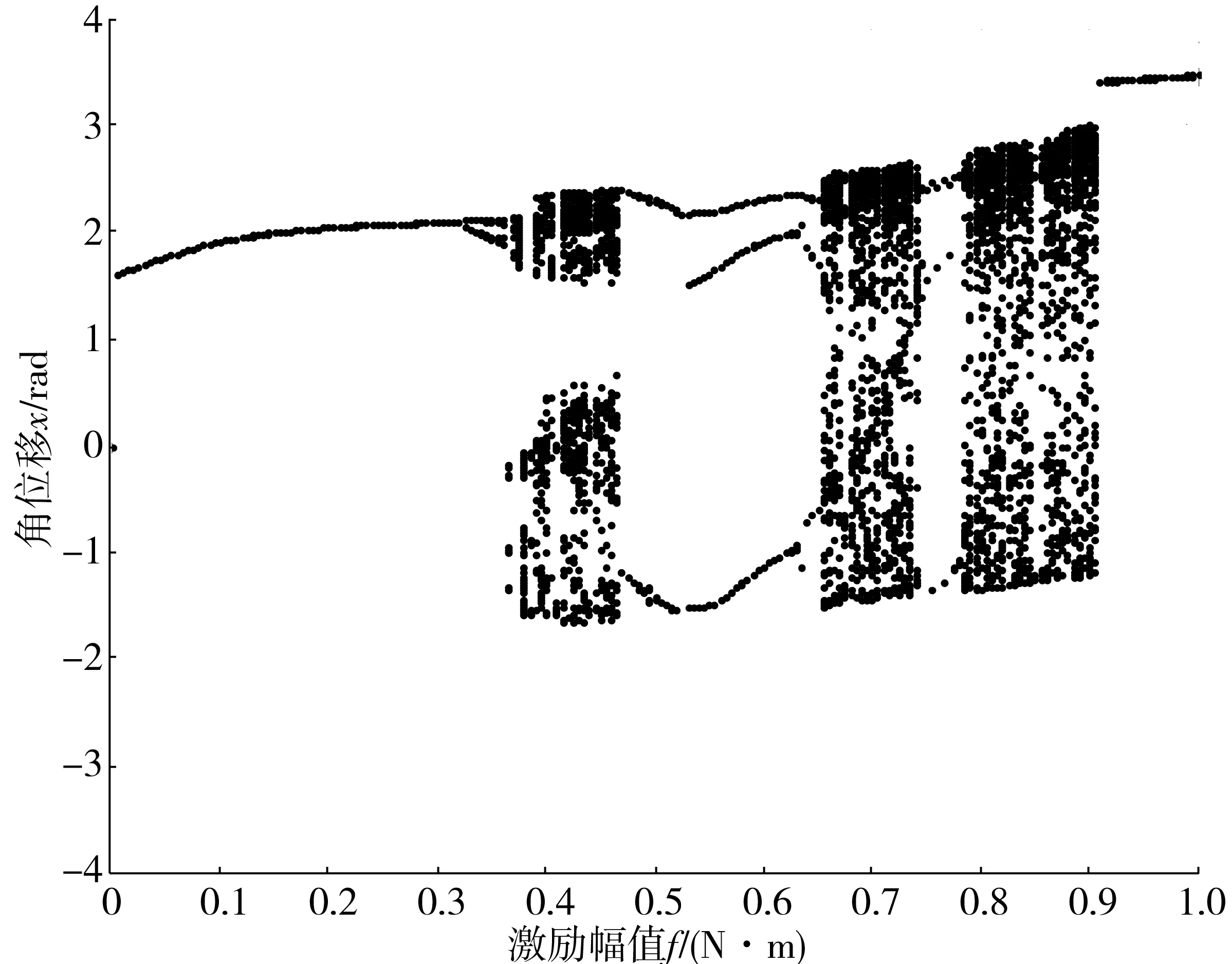
图7 f为控制参数时的系统分叉Fig. 7 Bifurcation diagram of the system when f is thecontrol parameter
从图7中可以看出,当f为控制参数时,机电耦合非线性扭振系统表现出复杂的非线性振动现象[8]:当激励值f较小时(f<3.6),系统为1周期振荡;当激励值f增大到3.6~3.8区间,2周期振荡取代1周期振荡;当f>3.8时,控制参数f进一步增加,系统在倍周期分岔后进入混沌运动;当f>3.8时,机电耦合系统表现为周期运动与混沌运动交替存在。
便于更好的理解,选取3组数值对周期运动变为混沌运动的过程进行具体分析系统,分别选取控制参数f=2,f=3.2,f=4,如图6(b)。当ω=1.0时,控制参数f由0逐渐增加,横截同宿点横截交叉发生于f≥3.6处。图8~图10表示了3种情况下时域波形、相轨迹、庞加莱截面和幅值谱。f=2对应的点处于阈值曲线之下,没有达到混沌运动的前提条件,如图6。
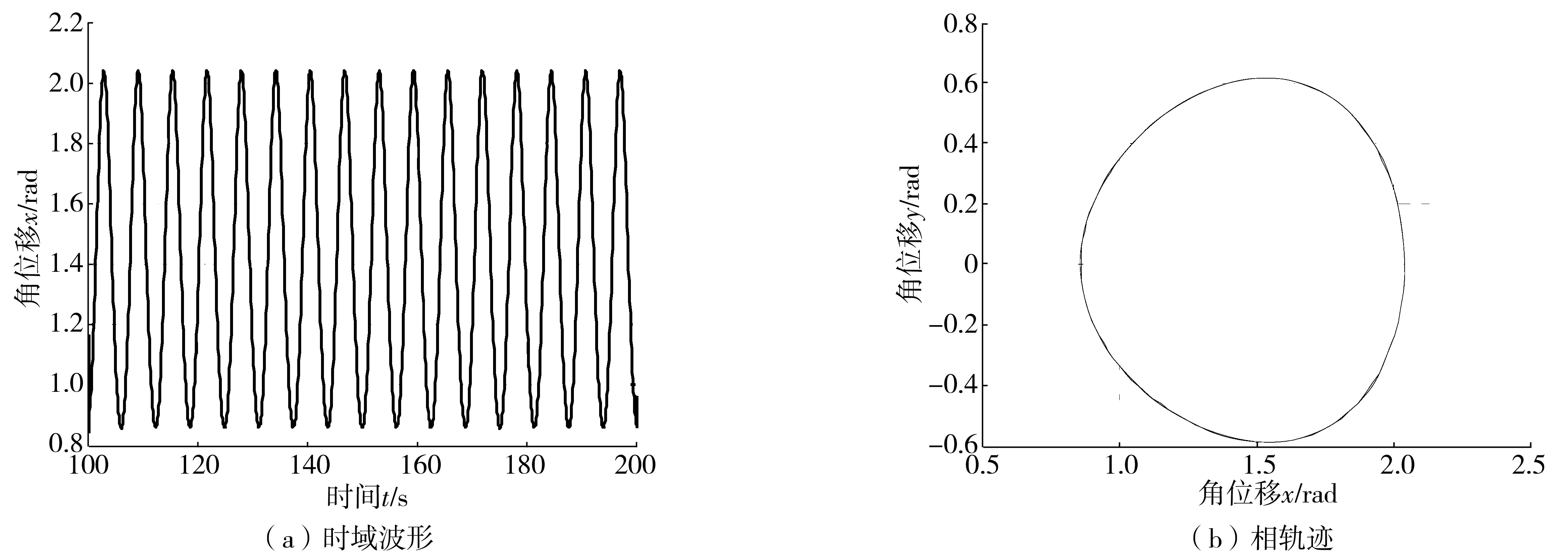
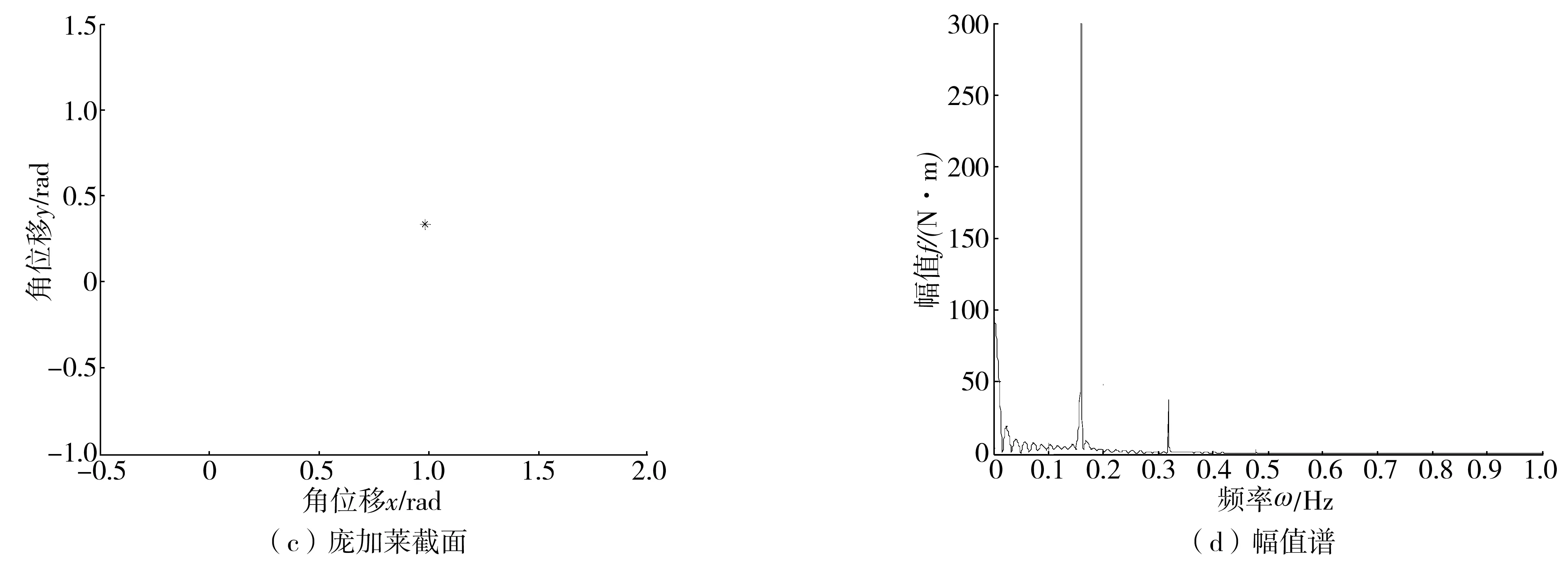
图8 f=2时1周期运动Fig. 8 1 period motion graph when f=2

图9 f=3.2时2周期运动Fig. 9 2 period motion graph when f=3.2

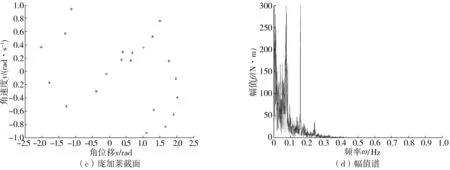
图10 f=4时混沌态Fig. 10 Chaotic state graph when f=4
由图8可以看出,f=2时,机电耦合扭转系统为1周期运动;当f开始增大并超过临界阈值,系统开始失去稳定性,并存在发生混沌运动可能性。从图9可以看出,f=3.2时,此时运行工况点处于阈值曲线之上,系统运动为2周期运动,系统发生倍周期分岔,但并未发生混沌运动。从图10可以看出:f=4时,运行工况点处于阈值曲线之上,进入如图7中的混沌区域,其计算结果如图10;时域波形并无周期性,相轨迹为多个交叉的环形圈,庞加莱截面图具有杂乱无章的多个点,频谱分析结果具有能量集中区域,这种现象表明该情况下系统发生混沌运动[9-10],这与我们之前Melnikov方法解析得到的结果是一致的。
5 结 论
以永磁同步电机的机电复合传动系统为研究对象,考虑机电耦合关系,建立永磁同步电机的电磁转矩模型,并通过非线性动力学理论得到电磁参数作用下的机电耦合参数振动界限以及规律。分析得到如下结论:
1)产生非线性振动的主要原因是由于车用永磁同步电机扭转角引起的电磁激励。
2)考虑机电耦合作用,扭转振动系统的固有特性与电机的运行状态以及结构参数相关,且在某些情况下,固有频率有较大的降幅。
3)考虑到车用电机采用弱磁控制,并且固有频率受到内功率因数角的影响,因此车用永磁同步电机需要合理控制内功率因数角的范围。
4)纯电动拖拉机机电耦合传动系统的控制参数激励值f逐渐增大时,系统具有周期、拟周期和混沌等复杂的动力学行为。当出现非线性振动时,机电耦合传动系统受到非周期冲击干扰力作用,产生较大强度动载荷并引起非线性扭振,严重影响纯电动拖拉机机电耦合传动系统可靠性和耐久性。因此,应避免纯电动拖拉机在低速重载工况下长时间运行。

