预应力混凝土连续梁桥动力特性及影响因素分析

任 翔，谭 潇，宋 飞，齐海鹏，马 敏

(西安科技大学 建筑与土木工程学院，陕西 西安 710054)

0 引 言

近年来，桥梁荷载试验已成为桥梁结构状态评定最直接的方法，被广泛应用于新建桥梁交、竣工验收中。而桥梁动载试验的目的是通过在脉动荷载和跑车荷载下测试结构的自振频率、阻尼比等动力特性来对桥梁状态进行评定。大量动载试验表明，动载试验实测的桥梁频率普遍高于理论计算结果[1-5]，尤其是结构动态评定中特别关注的结构一阶频率(基频)。针对此问题，不少学者进行了研究。夏樟华等[6]研究了结构中预应力张拉力大小、钢束形状及布置位置对动力特性的影响，得到结论：预应力张拉力大小对频率有一定的影响，钢束形状、布置位置则影响较小；郑尚敏等[7]研究了体外预应力的张拉力、锚固位置及钢束截面面积对自振频率的影响，得出3个因素均对自振频率影响较小的结论。这些研究多集中于研究预应力张拉力大小、钢束形状、钢筋布置位置对梁动力特性的影响。笔者以一座新建连续梁桥成桥荷载试验为背景，首先对比分析桥梁结构一阶频率实测值和理论计算值的差异，然后分别研究主梁纵向普通钢筋、预应力钢筋、护栏、混凝土动弹性模量等4个因素对结构一阶频率的影响，获得各影响因素对结构频率影响的显著程度，为准确地计算桥梁动态响应及评定桥梁动态响应提供了重要的参考依据。

1 工程概况

研究的新建预应力混凝土变截面连续箱梁桥主桥跨径组合为(48 + 80 + 48)m，横断面为单箱单室结构，边支点及跨中截面梁高2.3 m，主墩中心处梁高4.8 m，单幅箱梁截面顶板宽 12.75 m，标准厚度为 0.28 m；翼缘悬臂长 3 m，厚度从端部18 cm线形渐变为腹板根部60 cm；底板宽6.75 m。箱梁采用纵向、竖向预应力体系。主桥下部结构采用钢筋混凝土矩形实体式桥墩，钻孔灌注桩基础。上部结构采用C50混凝土，下部结构采用C40混凝土。桥梁立面布置如图1。

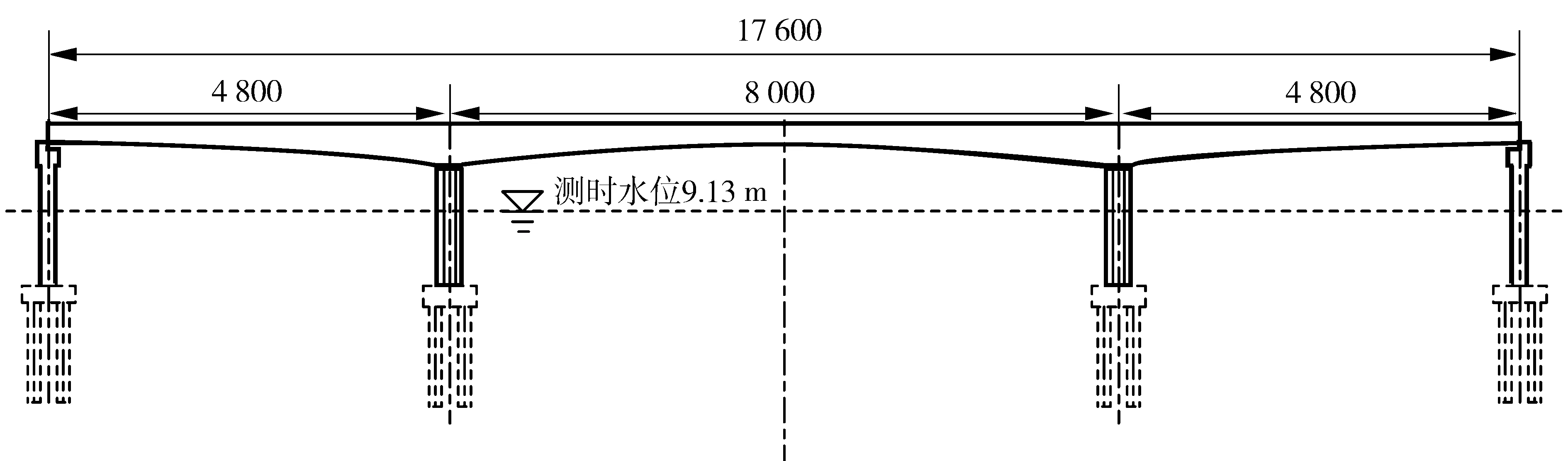
图1 主桥立面布置(单位：cm)Fig. 1 Layout of main bridge elevation

2 荷载试验方案及结果

自然环境激励技术是一种有效的利用自然环境激励响应提取结构振动脉冲响应的技术[8-9]，在中断交通通行的条件下，基于风和地面微振等环境因素的激励，测试桥梁结构频率、阻尼等动力特性。对新建桥梁进行现场动载试验测试，激振方法为自然环境激励法，试验一阶频率及振型的采集使用DH610高精度超低频加速度传感器，其结构动态试验测试传感器的布置示意如图2。

图2 测点纵向布置(单位：cm)Fig. 2 Vertical layout of measuring points

桥梁自振频域曲线测试结果(中跨跨中测点)见图3，一阶振型见图4。

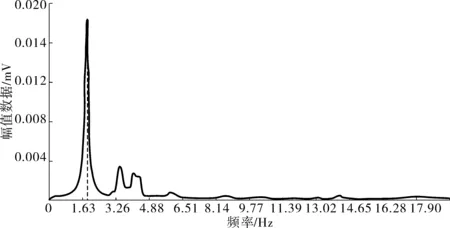
图3 自振特性测试频域曲线Fig. 3 Frequency domain curves of natural vibration characteristictest

从桥梁动态测试结果可以看出，一阶频率为1.760 Hz，一阶振型为对称竖向弯曲振动。

3 有限元模型

采用有限元软件Midas Civil 建立空间动力分析模型(图5)，全桥共采用梁单元61个，边界条件按照设计图纸中支座的类型和布置就行设置，将二期荷载和自重转换为质量进行模态分析。模型中未考虑普通钢筋、预应力钢筋、护栏和混凝土动弹性模量的影响。

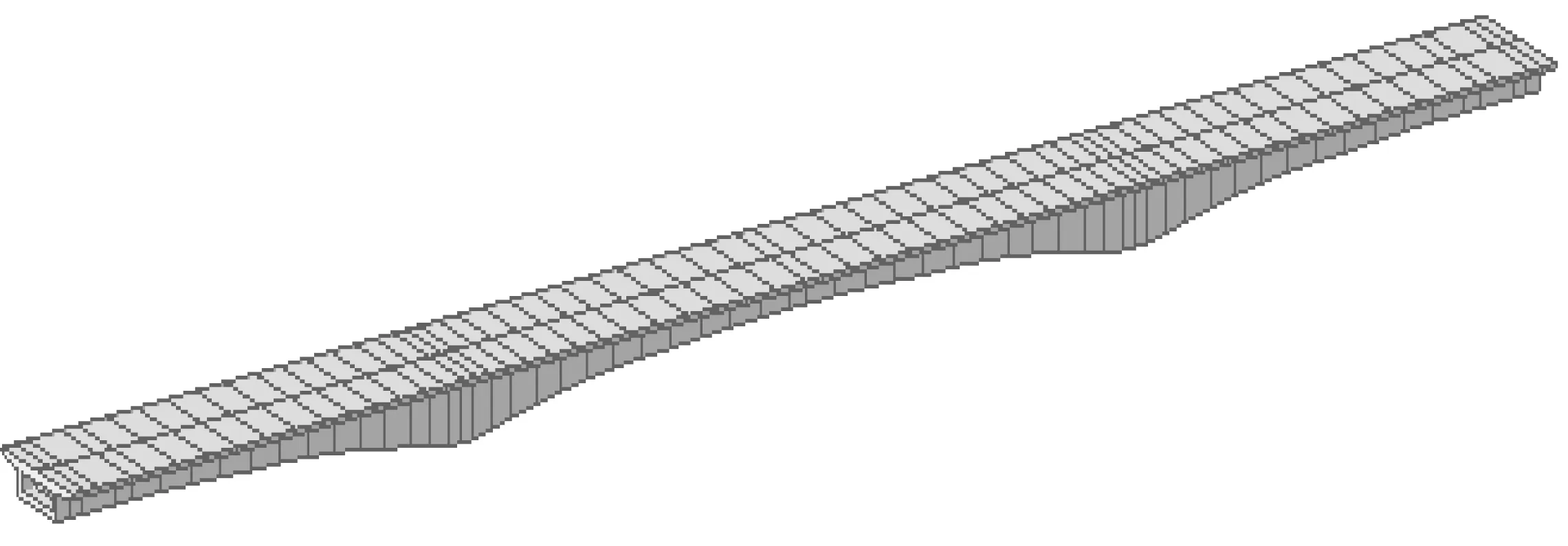
图5 三维空间模型Fig. 5 3-D model

从图6可知，桥梁理论计算一阶频率约为1.395 Hz，周期为0.717 s，其振型与实测振型一致。

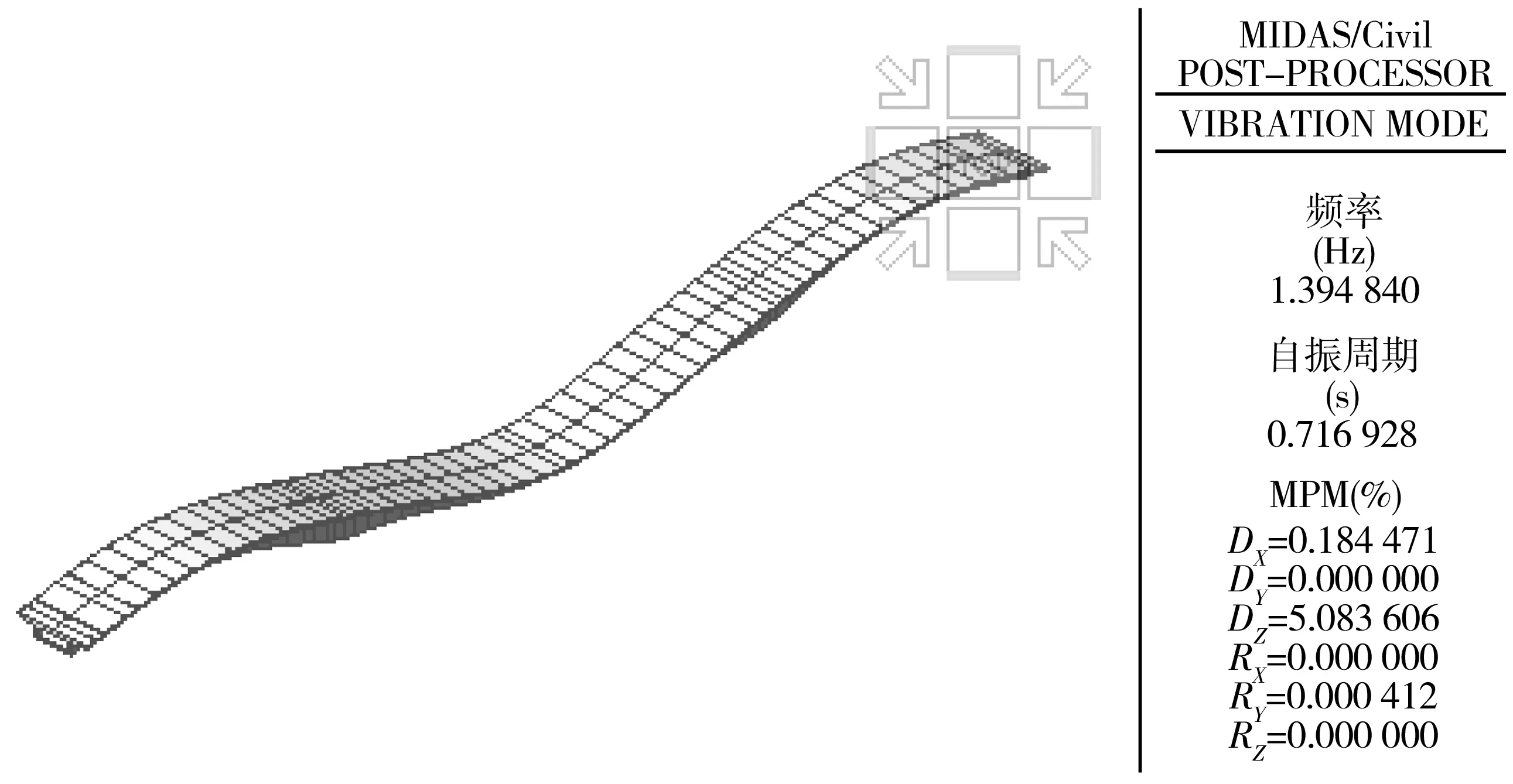
图6 一阶振型Fig. 6 Vibration type of first-order frequency

4 动力特性影响因素分析

桥梁一阶频率实测值为1.760 Hz，理论计算值为1.395 Hz，二者偏差约为21%，偏差较大。为了探明实测一阶频率和理论计算频率偏差产生的原因，建立6种不同的计算模型，其中模型1为对比分析的基准模型，而模型2～模型6分别考虑普通钢筋、预应力钢筋、护栏及混凝土动弹性模量等4个影响因素对桥梁动力特性的影响，详见表1。

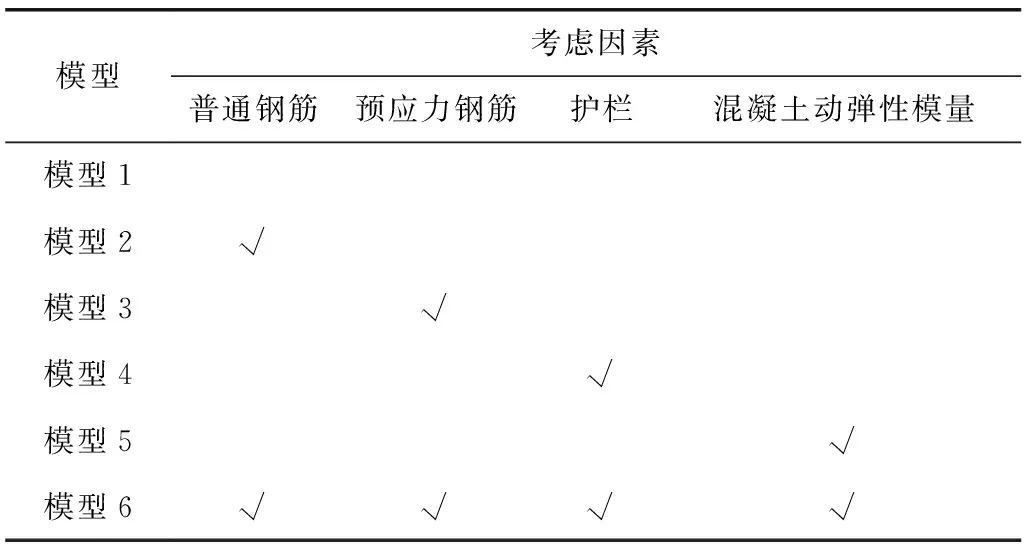
表1 模型设置Table 1 Model setting

4.1 普通钢筋的影响

分析中，仅考虑了纵向普通钢筋对结构动力特性的影响。为了简化建模过程，采用调整截面刚度的方法来考虑纵向普通钢筋的影响，即将实际面积的钢筋换算成一定面积(换算截面)的混凝土材料，根据换算后的截面来调整模型刚度。

钢筋的刚度按式(1)等效为混凝土刚度：

Ieq=Icon+Ascx2=Icon+αESAsx2=Icon+αESIs

(1)

式中：Ieq为将钢筋等效换算成混凝土截面惯性矩；Icon为换算前原混凝土截面惯性矩；Asc为换算钢筋截面面积；αES为换算系数，αES=Es/Ec(Es为钢筋弹性模量；Ec为混凝土静弹性模量)；Is为钢筋对截面中性轴惯性矩；As为钢筋截面面积；x为钢筋形心和钢筋等效为混凝土截面的形心到截面中性轴距离。

换算截面如图7。

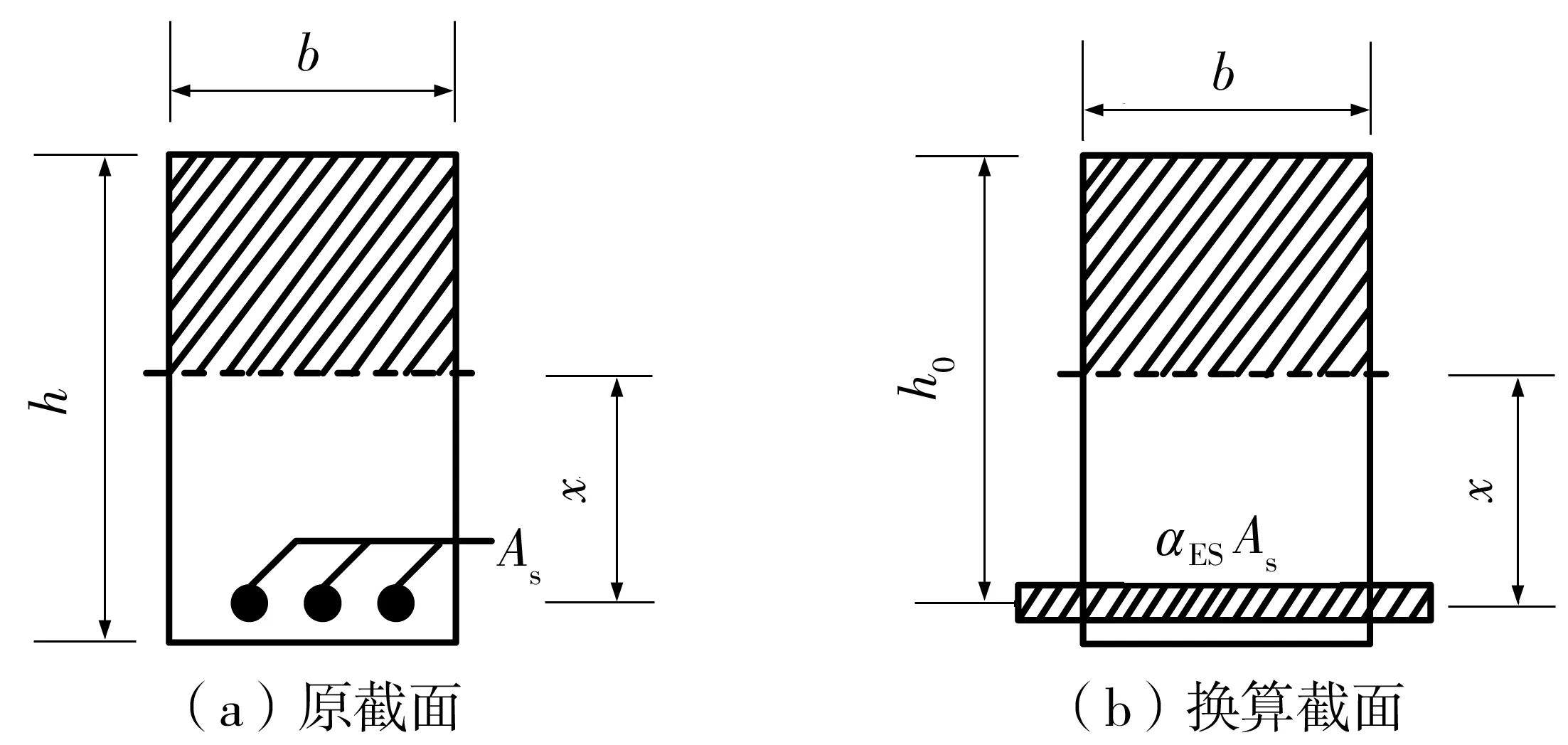
图7 截面换算Fig. 7 Section conversion

由图8可见，考虑了纵向普通钢筋影响后结构的一阶频率为1.416 Hz，与模型1一致。

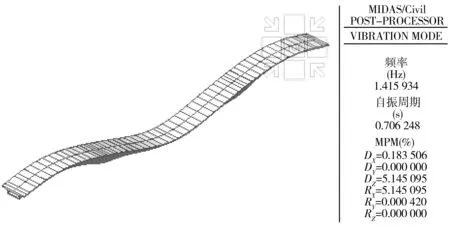
图8 模型2的一阶频率及振型Fig. 8 First-order frequency and vibration type of model 2

4.2 预应力钢筋及张拉力的影响

通过在模型中添加预应力钢筋、张拉预应力的方式来考虑预应力钢筋对桥梁动力特性的影响。由图9可见，考虑预应力钢筋影响后结构的一阶频率为1.413 Hz，振型与模型1一致。

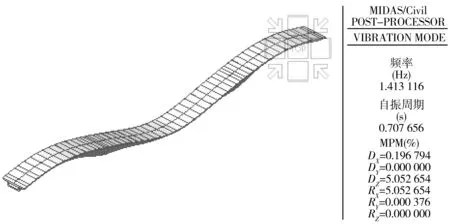
图9 模型3的一阶频率及振型Fig. 9 First-order frequency and vibration type of model 3

4.3 护栏的影响

为了避免桥梁变形造成桥面系护栏破坏，通常桥面系护栏在沿桥走向上分段预留竖向缝，护栏自身刚度对桥梁竖向刚度影响较小，因此，仅考虑护栏的质量对桥梁振动频率的影响。由图10可见，考虑了护栏质量影响后的结构一阶频率为1.384 Hz，一阶振型与模型1一致。

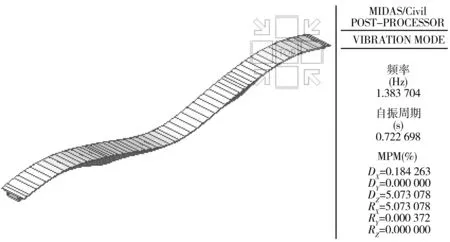
图10 模型4的一阶频率及振型Fig. 10 First-order frequency and vibration type of model 4

4.4 混凝土动弹性模量的影响

桥梁结构设计时，采用混凝土静弹性模量进行结构计算，而工程结构动力特性分析中，混凝土的动弹性模量要比混凝土静弹性模量大很多，因此，采用混凝土动弹性模量进行结构计算更为接近实际状态。同时，对桥梁进行动力特性分析时，需要将混凝土静弹性模量转换成动弹性模量，其相互关系的公式为[10]：

Ej=κEd

(2)

式中：Ej为混凝土静弹性模量；Ed为混凝土动弹性模量；κ为换算系数，当混凝土粗骨料粒径分别为5～20 mm、5～30 mm时，κ分别为0.901、0.857。

模型1中，C50混凝土静弹性模量为3.45×104MPa，而现场实测的桥梁主梁混凝土静弹性模量Ej=4.3×104MPa，远大于C50混凝土静弹性模量。根据式(2)得到主梁混凝土动弹性模量Ed=4.77×104MPa，因此模型5采用根据现场实测混凝土静弹性模量计算得到的混凝土动弹性模量4.77×104MPa。

图11为模型5的结构一阶模态，可以看出，考虑混凝土动弹性模量后结构一阶自振频率为1.634 Hz，一阶振型与模型1一致。

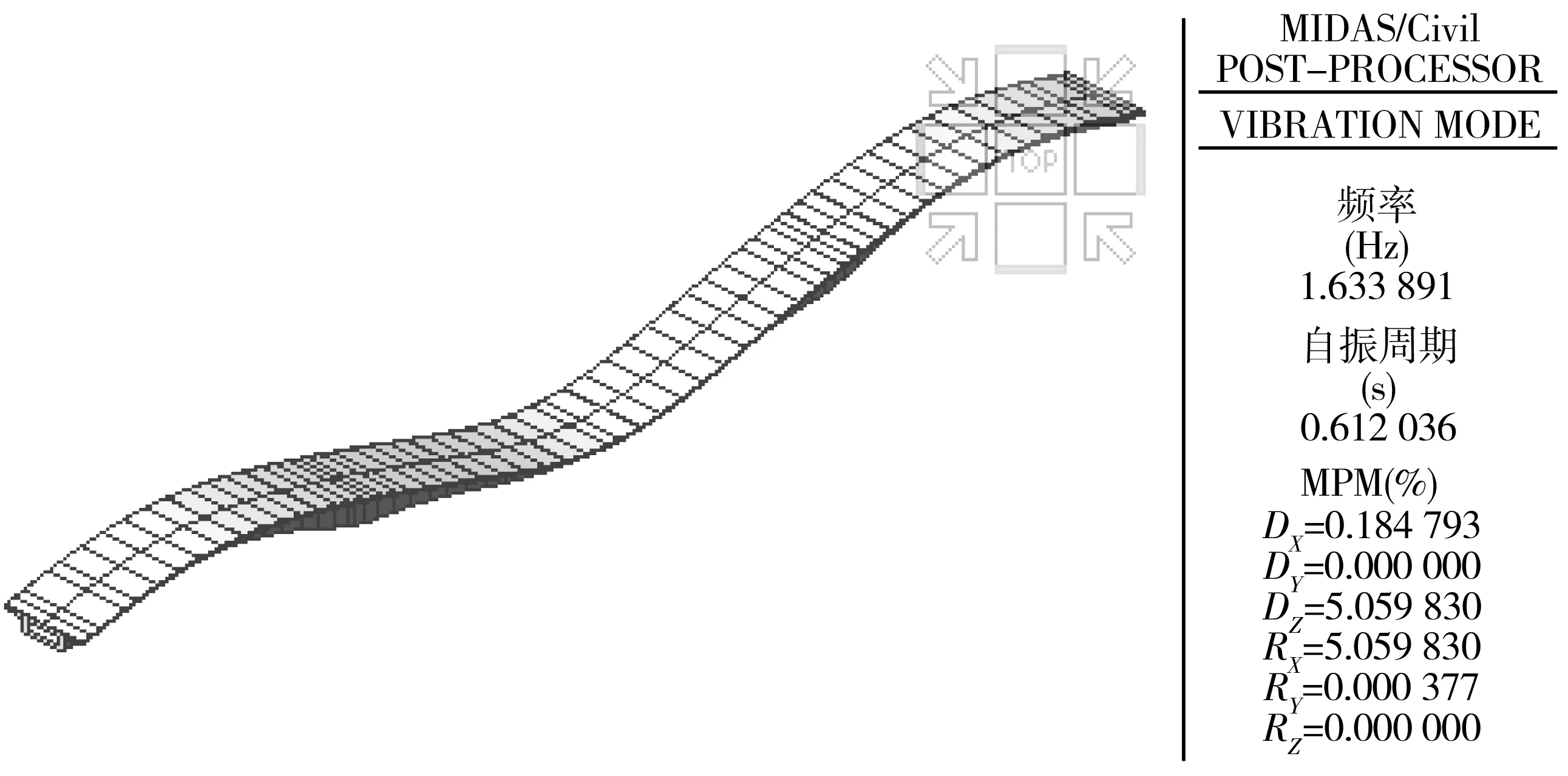
图11 模型5的一阶频率及振型Fig. 11 First-order frequency and vibration type of model 5

4.5 4因素综合影响

将普通钢筋、预应力钢筋、护栏以及混凝土动弹性模量同时计入有限元模型中进行计算，综合考虑4个因素后，结构的一阶频率为1.684 Hz，振型与模型1一致。

4.6 对比分析

以模型1计算结果为基准，模型2～模型6计算结果与其进行对比，找出影响桥梁结构一阶频率最为显著的因素。图12显示了所有模型的一阶频率计算值和实测值。

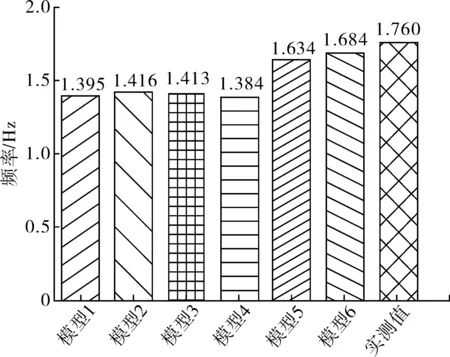
图12 一阶频率的计算值与实测值Fig. 12 Calculated and measured values of first-order frequency

由图12可见，模型1～模型6的一阶频率计算值均小于实测值，模型5和模型6的一阶频率计算值与实测值较为接近，二者仅差7%，表明混凝土动弹性模量是影响桥梁动力特性最为显著的因素，其余因素影响较小。该结论也由模型6的计算结果得到了证实。

5 结 论

1)在桥梁结构动力特性理论分析时，未计入混凝土动弹性模量是引起桥梁一阶频率计算值和测试值偏差较大的主要原因之一。考虑混凝土动弹性模量影响后的理论计算结果与实测值偏差较小。

2)建议利用桥梁动荷载试验结构基频评定结构刚度时，应在有限元模型中计入混凝土动弹性模量，且在新建桥梁动态试验中，应测试混凝土的实际强度间接获得混凝土弹性模量，转化成动弹性模量后计入有限模型，更为接近实际状态，分析结果更为准确。