基于损伤性能函数的桥梁结构损伤识别

陈东军，李天华，彭 凯，张可佳，林洁琼，白文英

(1. 重庆交通大学 土木工程学院，重庆 400074; 2. 新疆城建试验检测有限公司，新疆 乌鲁木齐 830000; 3. 中建新疆建工路桥工程有限公司，新疆 乌鲁木齐 830054)

0 引 言

结构局部损伤会导致结构单元/构件的刚度下降，引起识别出的结构动力特性如自振频率、模态振形等发生相应变化，从而可以通过结构动力特性的测定实现结构动力损伤识别[1]。根据对结构损伤识别过程中随机因素的不同处理，结构动力损伤识别可以大体分为确定性方法和不确定性方法。目前结构动力损伤识别大多是在确定性动力激励条件下基于模态分析、模型修正或时域数据分析的确定性方法[2-3]。

事实上，由于外部荷载、结构自身几何物理性质、测试系统、环境因素以及分析模型等均不可避免地包含随机性，结构损伤识别必然带有不确定性，使得确定性识别方法对于结构早期损伤、局部损伤识别的可靠性和鲁棒性难尽人意[4]。G. W. HOUSNER 等早已指出[5]：基于概率统计原理的结构健康监测的不确定性方法研究，可望为解决大型土木工程结构健康监测问题提供普适性手段。因此，结构损伤识别的不确定性方法研究具有重要的发展前景和价值，近年来取得了一些进展：L. PAPADOPOULOS等[6]为改进结构损伤识别的鲁棒性，基于随机有限元模型，考虑由于测试过程试验误差导致的模态频率和振型的不确定性，采用Monte-Carlo随机模拟方法计算待识别参数误差的协方差矩阵，根据识别参数的概率密度函数定义结构损伤的概率因子及其置信区间；Y. XIA等[7]考虑实测结构动力响应数据及有限元模型的随机噪声效应，提出基于频率变化的随机损伤识别模型，其中结构在完好状态和损伤状态下的刚度参数统计特征采用摄动法计算并用Monte-Carlo方法进行校核，然后基于两种状态下刚度参数的概率密度函数来估计结构的损伤概率；T. SAITO等[8-9]采用结构在完好和损伤状态下的实测振动数据，建立了结构损伤存在性、位置和程度的概率性估算方法框架，并通过人为引入不同损伤状态的5层钢框架的振动台白噪声激励试验对该方法进行了验证；D. WANG等[10]采用基于相关性分析的算法估计Lamb波激励下铝板中损伤存在的概率；K. ZHANG等[11]为了避免确定性损伤识别方法中由于测试过程随机性导致的损伤误报，提出未知激励下不确定性结构损伤识别的概率方法，该方法肇始于基于动力响应敏感性的结构物理参数和激励输入确定性损伤识别方法，其结构损伤概率由损伤状态下识别出的结构刚度参数小于完好状态下对应参数的概率来定义；I. BEHMANESH等[12]采用贝叶斯(Bayes)有限元模型修正方法研究Dowling Hall人行桥的概率损伤识别，该桥加装有持续的环境激励下加速度响应监测系统，数据每小时记录一次或由振动触发记录，结构损伤通过在桥面局部附着混凝土块进行模拟，识别结果与实际情况吻合较好；R. PASQUIER等[13]比较了贝叶斯推断和误差域模型证伪(Error Domain Model Falsification, EDMF)方法进行结构参数识别的鲁棒性和外插精度，结果表明在系统误差存在的条件下前者优于后者；I. BEHMANESH等[14]基于结构不同振动模态对模型误差敏感性的差别，针对结构损伤识别的模型修正法提出了选取最优模态子集和最优模态残余权重以减小模型误差影响的方法。

综上可见，现有基于概率的结构损伤识别研究成果，主要针对试验测试过程、结构有限元模型等方面的随机性及其效应开展研究，涉及的荷载形式主要有确定性激励、白噪声和环境激励等，而真实服役荷载条件下的不确定性结构损伤识别研究还较少报道。事实上，直接基于运行状态下的结构振动测试和损伤识别具有直接利用使用荷载的有效激励、不必中断服役、结构运行状态直接真实、测试成本低廉等优点，理论和应用上均更加便于在线健康监测[3，15]。为此，笔者在前述研究基础上，提出利用随机行车激励下的实测桥梁动力响应开展结构损伤识别的概率方法，对结构加速度响应进行时域分段频谱分析，采用概率统计方法获得频谱统计特征，并基于可靠度理论构建表征结构性态演化的损伤性能函数，最后利用损伤性能函数计算结构损伤概率，数值算例所得结果与结构损伤状态前后发展趋势定性一致。

1 带裂缝混凝土板的动力响应计算

1.1 两跨连续梁板桥模型

为模拟随机参数行车激励下的桥梁结构动力响应，选取较为简单的板梁桥作为研究结构对象，并通过在其控制截面引入裂缝来模拟结构损伤，对比开裂前后结构动力响应特性的变化，开展结构动力损伤识别。为方便研究，取2 m × 40 m的两跨连续梁板，其断面宽10 m、高1 m，梁板混凝土材料弹性模量为8 × 1011Pa，泊松比取0.2，材料密度取2 250 kg/m3。采用ANSYS分析软件，采用Solid45实体单元建立梁板有限元模型。带裂缝梁板纵向剖面、横断面分别如图1(a)和(b)，无损伤、2 m和8 m长裂缝对应的a值分别取0、2和8，裂缝高度h=0.5，有限元模型如图2。动力模拟中暂不计入阻尼影响。

常用的混凝土板裂缝有限元数值模型有[16]：离散裂缝模型、弥散裂缝模型和断裂力学模型。笔者引入裂缝作为混凝土板的损伤形式，采用较简单的离散裂缝模型，用分离的单元边界模拟裂缝面。如图1(a)，裂缝位置距离板左端21 m；控制点位置靠近裂缝，距离板左端20 m。

图1 带裂缝梁板示意(单位：m)Fig. 1 Schematic of the slab with a crack

图2 梁板的ANSYS有限元模型Fig. 2 ANSYS finite element model for the slab

1.2 随机参数行车激励模拟

桥梁上实际行驶的车辆，其尺寸、载重、速度、运行路线等参数均具有随机性，如再考虑路面的不平整导致车辆对桥梁冲击动力效应的不断变化，则考虑单个车辆一次行驶桥梁全长的过程中车辆对桥梁的动力激励，应视为在时间上连续分布、空间上连续移动的随机荷载。为此，在时间和空间上对此时空变化随机荷载进行离散，即采用幅值随机分布的时空变化脉冲序列在梁板上以一定速度(取10 m/s)通过梁板桥面。匀速移动随机脉冲序列利用Excel软件的随机数自动生成功能产生，取脉冲荷载均值为100 kN，离散系数取0.5。考虑到后续数值计算和数据处理耗时很多，暂考虑生成10个随机序列用于数值模拟。总长度为80 m的模型梁板纵向均匀划分成80个有限单元，则每个单元纵向长度为1 m。设荷载移动速度为10 m/s，则荷载通过一个单元长度所需时间为0.1 s，也即每个离散随机脉冲持续时间为0.1 s。一次行车过程共离散成80个随机脉冲组成的荷载序列，持时共计8 s。随机脉冲序列的典型时域分布如图3。

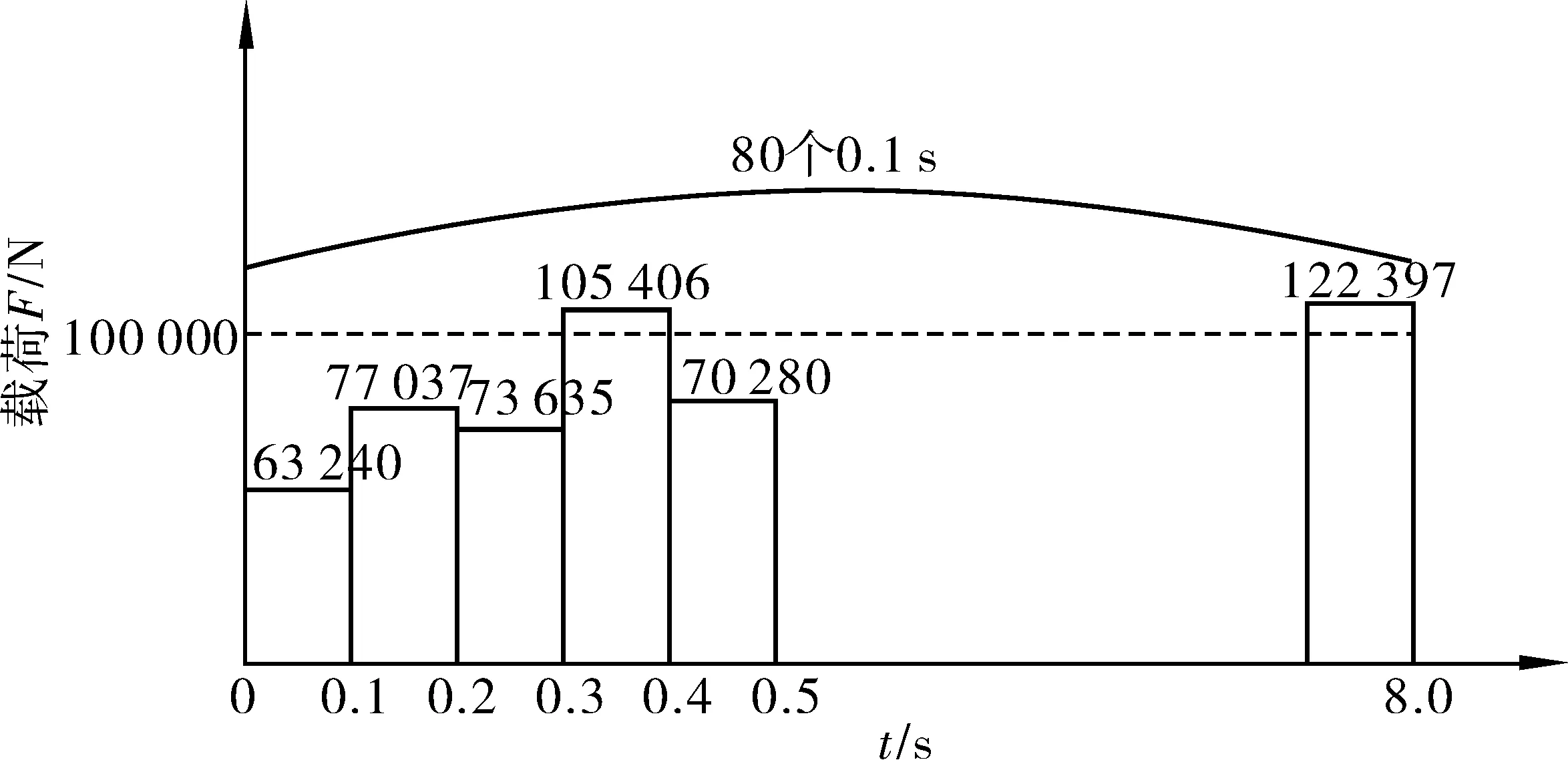
图3 随机脉冲序列Fig. 3 Random pulse sequence

在桥梁横向，车辆的路线位置也具有随机性，可能居中也可能靠边。如图4，分别考虑车辆荷载位于桥面横向不同位置：①荷载中心位于梁板截面对称中心；②荷载中心距离梁板截面中心2 m；③荷载中心距离梁板截面中心4 m。

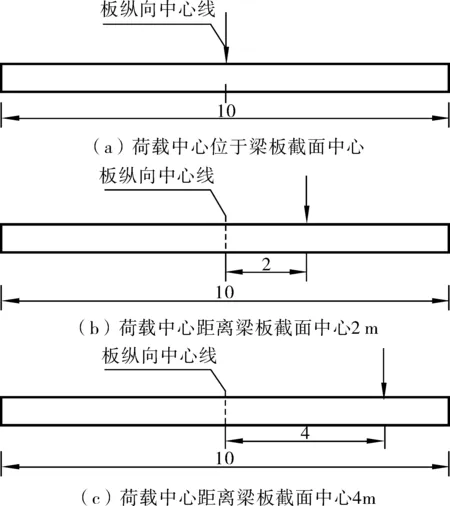
图4 荷载作用位置(单位：m)Fig. 4 Different loading positions

根据前述参数的变化情况，拟定随机行车激励模拟的随机脉冲序列工况示例如表1。表1给出对应随机脉冲序列1的9个工况，则10个时空变化随机脉冲序列一共有90个模拟工况，对应模拟90次参数随机变化的桥梁全长行车激励。

表1 行车激励模拟工况定义示例Table 1 An example of the running vehicle excitation case

注：工况定义编号含义，如工况1-1-1，第一个“1”表示随机脉冲序列1，第二个“1”表示荷载中心横向位置，第3个“1”表示结构开裂状态，依此类推定义10个随机脉冲序列下的工况。

2 梁板桥控制点的频谱响应统计

采用ANSYS数值求解各随机脉冲序列模拟工况下梁板桥结构在控制点位置的行车全程加速度响应时程，典型结果如图5。

图5 加速度时程曲线Fig. 5 Acceleration time-history curve

2.1 加速度微元分段和频率点统计

对每一个工况下求得的桥梁控制点加速度时程曲线以相等间隔(取0.5 s)进行时间分段，共划分成16个时间段，如图6。采用频谱分析软件Seismosignal对各时间微元段加速度时程进行频谱分析，得到其频谱图，如图7。对每个时间段的频谱图，均按幅值由大到小提取前8个频率值。按前述一个随机脉冲序列模拟工况持续时间8 s计，则一次桥梁全长行车激励下采集到的控制点频率值共有16×8=128个。将这一个工况下的128个频率值作为一个样本，然后进行统计分析，找出对行车激励参数随机性不敏感的特征值。从一个工况下各时间段的频谱中选取的频率值样本如表2。

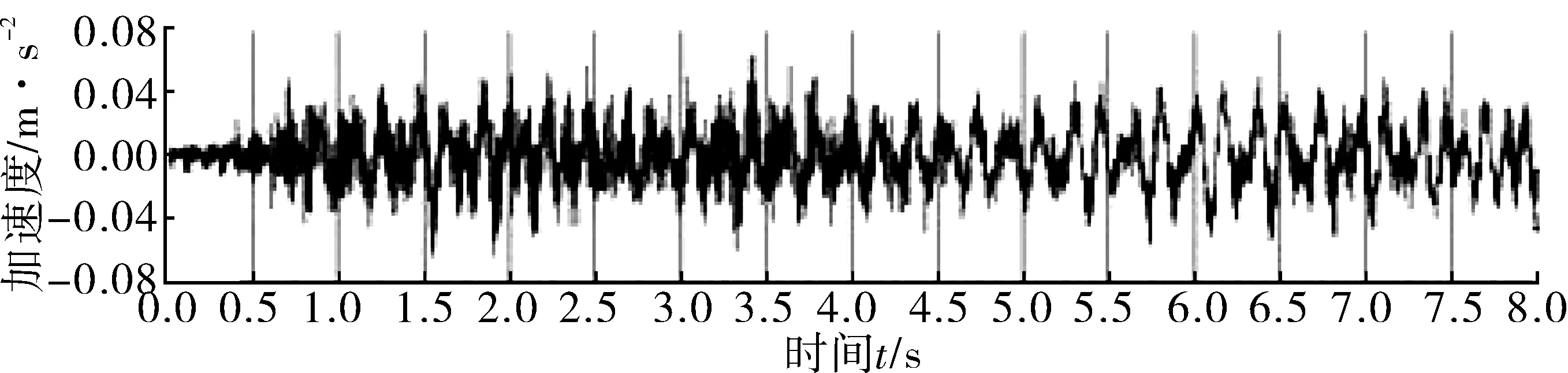
图6 加速度响应时程微元分段Fig. 6 Microelement segmentation of acceleration response time-history

图7 微元分段频谱Fig. 7 Frequency spectrum corresponding to microelementsegmentation

时间段号频率/Hz19.7746.8856.6493.75130.86138.67181.64224.6125.8625.3946.8856.64193.75132.81138.67224.6135.8627.3446.8856.64193.75132.81138.67181.6445.8646.8856.6493.75138.67181.64222.66230.4757.8127.3446.8856.64193.75138.67183.59230.4767.8127.3446.8856.64193.75132.81181.64230.4775.8627.3446.8893.75132.81138.67181.64224.6185.8627.3446.8856.64193.75130.86138.67218.7595.8627.3446.8856.64193.75103.52138.67218.75105.8627.3446.8856.64193.75103.52132.81218.75115.8627.3446.8856.64193.75132.81138.67230.47125.8646.8856.6493.75103.52132.81218.75230.47135.8627.3446.8856.64193.75103.52132.81218.75145.8627.3446.8856.64193.75103.52134.77218.75157.8127.3446.8856.64193.75103.52132.81218.75167.8127.3446.8856.64193.75103.52138.67218.75

由表2可见，不同时间段的频谱中，多个频率值前后多次重复出现。对一个样本中各重复出现的频率值进行重复几率统计(即将其重复次数除以样本量)，在时空变化随机脉冲序列1下分别对工况1-1-1、1-1-2、1-1-3的样本统计结果见表3，表3中只列出重复次数大于2的频率点。

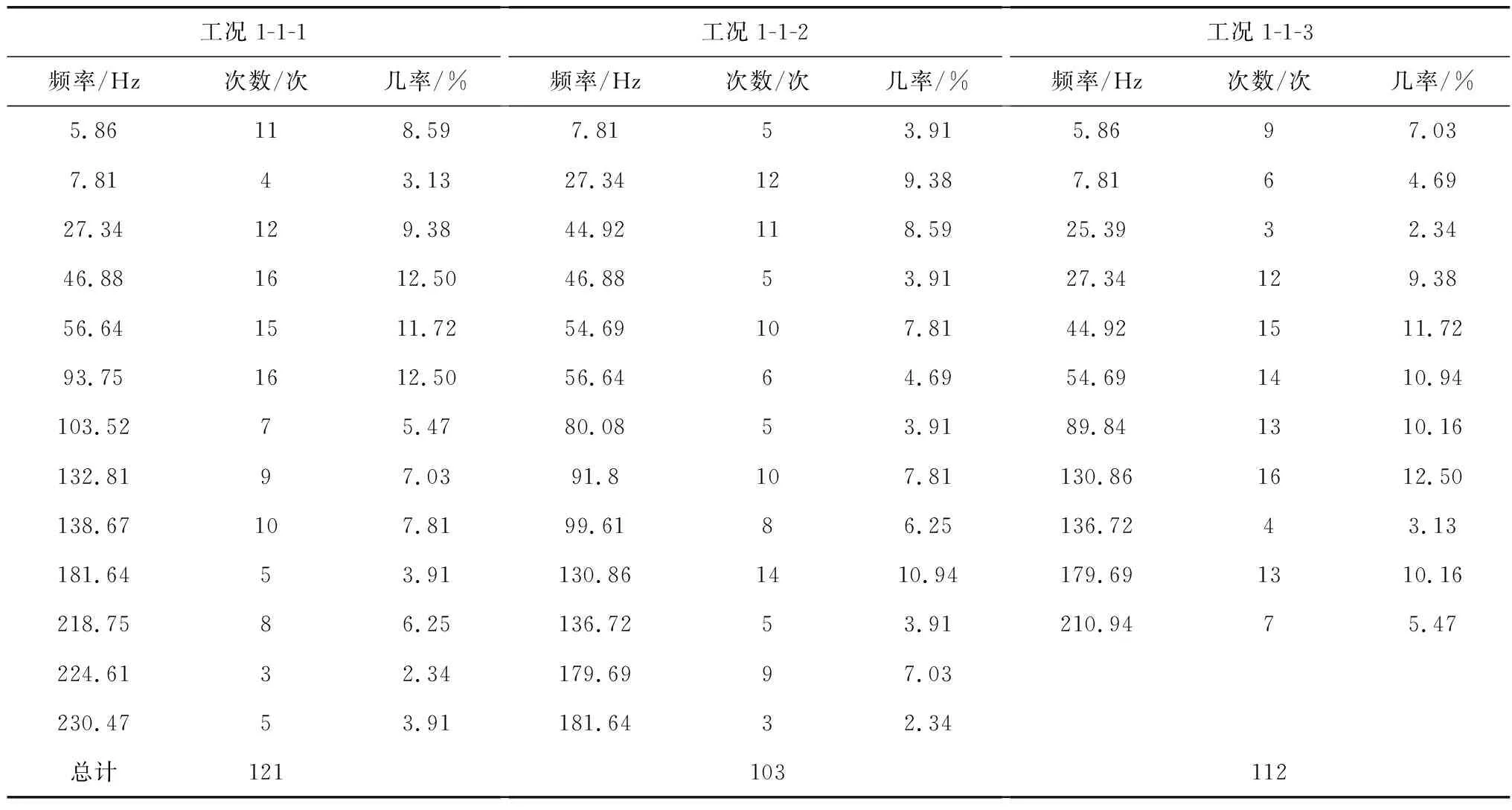
表3 频率重复几率统计Table 3 Probabilities of the repeated frequency values

如前述，桥梁上行车激励可简化抽象为时空变化的随机脉冲序列，结构在脉冲激励后的振动为自由振动。控制点加速度响应频谱体现的是结构的自振特性，而结构自振特性在结构自身几何物理特性保持稳定(即无损伤发生或损伤无发展)的条件下也应稳定不变。因此表2频率值样本中出现了多个前后多次重复的频率值。经与桥梁模态分析结果比对，这些频率值同时也是结构的自振频率值。可见一个样本中多次重复出现的频率值，其稳定性(即重复几率)对行车激励参数的随机变化并不敏感，而主要取决于结构自身几何物理性状和动力特性。另一方面，同一样本中，某一频率值稳定性越高，体现对应阶振型对控制点位置振动响应贡献的显著性越强。

2.2 频率稳定点的提取

将表3中同一频率样本多次重复出现的频率值称为频率稳定点，并将时空变化随机脉冲序列1下的频率稳定点与各自对应的结构自振振型阶数绘制成图，对比3种不同的损伤状态下结构频率稳定点的分布规律，如图8。

图8 频率稳定点分布Fig. 8 Distribution of frequency stable points

从图8可看出，3种结构损伤状态对应的频率稳定点分布曲线大体上根据高度可排序为：结构状态1>结构状态2>结构状态3，且结构状态2相比结构状态3的对应曲线局部(中低频部分)明显要高，说明结构出现局部损伤后，总体而言频率稳定点分布曲线会下移，结构对应阶固有频率会发生不同程度降低。

另一方面，对无损伤、2 m长裂缝和8 m长裂缝3种状态下的桥梁结构进行模态分析，得到对应的前三阶固有频率，见表4。由表4可见，相比无损伤结构，当结构发生上述两种局部损伤时，其前3阶自振频率变化并不明显：两种损伤状态下的自振频率相比无损伤状态的降低比率，对一阶依次为4.1%、6.7%，对二阶依次为2.1%、3%，对三阶依次为0.2%、0.3%。考虑到识别系统的硬件和软件误差，则低阶频率对基于结构自振频率的确定性模态识别而言，其作为损伤指标的有效性存疑。

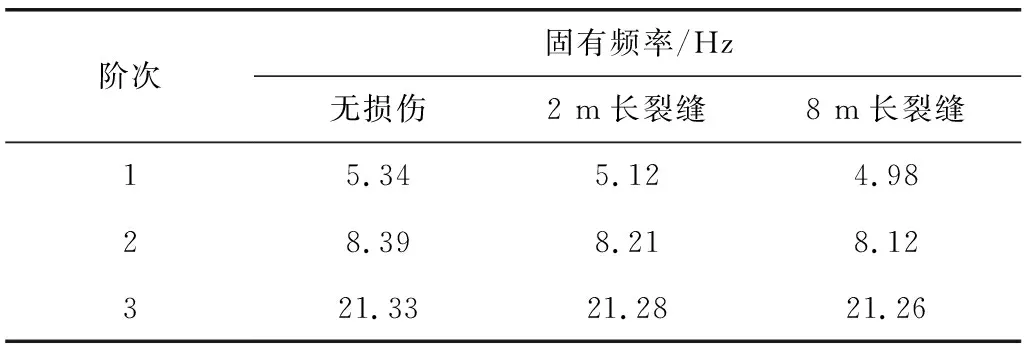
表4 3种状态梁的前三阶固有频率Table 4 The first three order natural frequency of beams under3 kinds of states

3 指征频率统计及性能函数建立

3.1 指征频率统计

根据前述频率值重复几率统计结果，可对一个样本中的实测频率值进行加权统计得到频率加权平均，如式(1)：

em=e1k1+e2k2++enkn

(1)

式中：em为频率加权平均；k1，k2，，kn为频率点重复几率；e1，e2，，en为频率值，n≤8。

表5列出了随机脉冲序列1下结构控制点频率依式(1)得到的频率加权平均。

从表5可以看到，结构从“无损伤”到跨中附近出现“2 m长裂缝”再到“8 m长裂缝”，其指定控制点位置的对应频率加权平均呈现明显的降低趋，其他随机脉冲序列下的这一趋势也稳定存在。可见频率加权平均值的变化趋势对行车激励参数的随机变化并不敏感。因此笔者提出以频率加权平均作为指示结构损伤情况的指征频率，用以代替常规的低阶自振频率。

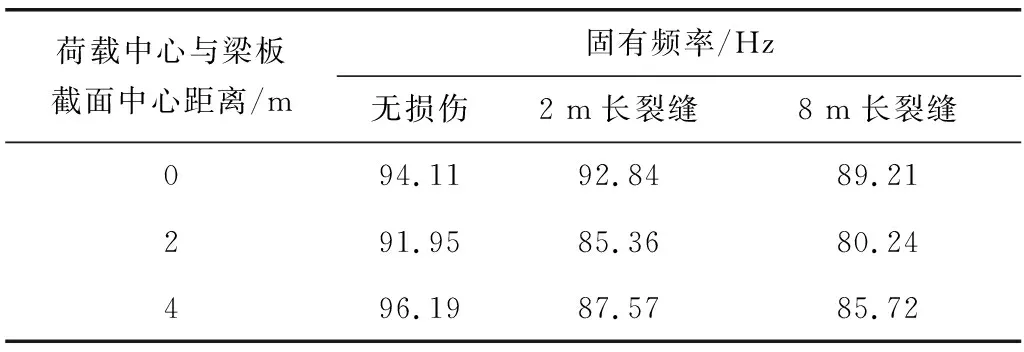
表5 随机脉冲序列1下控制点频率加权平均Table 5 Frequency weighted mean of control points under randompulse sequence 1

3.2 性能函数的建立

同一结构状态下指定控制点的指征频率会随着行车激励参数的随机变化而呈现随机分布的特性。因此，如果将指征频率视为确定量，按常规大小比较的方式来判别结构损伤，将难以得出科学合理的结果。为此，借助结构可靠度理论的相关成果[17]，将控制点指征频率视为随机变量，并将指征频率随结构状态变化而减小(或增大)视为随机事件，根据随机事件发生的概率来判别结构损伤状态，识别结果将更为符合实际。表6所列分别为结构从“无损伤”到跨中附近出现“2 m长裂缝”再到“8 m长裂缝”3种状态下指定控制点的指征频率在对应的30个工况下的取值。

表6 各工况下测点频率概率统计加权Table 6 Statistical weighting of the frequency probability of measuring points under various working conditions Hz

由表6可知，同一结构损伤状态下指定控制点的指征频率随着行车激励参数的随机变化而呈现随机分布的特性。经与常用分布模型比较，指征频率可用正态分布随机变量予以描述。

令“无损伤”、“2 m长裂缝”和“8 m长裂缝”3种结构损伤状态下指征频率随机变量分别为I1、I2和I3，则借助前述可靠度理论[17]建立结构损伤性能函数为：

D=ID-I0

(2)

式中：D为对应损伤状态指征频率ID的结构损伤性能函数；I0为无损伤状态指征频率。ID和I0均为正态分布随机变量，而D为ID和I0的线性函数，因此D也是符合正态分布的随机变量。

对功能函数D做一次观测，可能出现如下3种表征结构损伤状态的情况：

1)D=ID-I0<0,结构发生损伤。

2)D=ID-I0=0,结构状态无变化。

3)D=ID-I0>0,结构得到加固增强。

这样，就可以基于D=ID-I0<0这一随机事件发生的概率进行结构损伤识别。令

PD=P(D=ID-I0<0)

(3)

式中：P为D的概率分布函数；PD为结构损伤概率。定性而言，PD>50%即可视为结构发生了损伤，PD值越大则结构损伤程度越大。

3.3 基于性能函数的损伤概率识别

利用前述建立的损伤性能函数判断结构发生损伤的概率。由表6所列正态随机变量I1、I2和I3的样本值，并根据结构损伤性能函数D与ID的对应关系，可以分别统计I1、I2和I3(此处I1对应无损伤状态，I2和I3分别对应不同损伤状态)的平均值和标准差，进而算得不同损伤状态下D的平均值和标准差，再根据正态分布的性质由式(3)计算出结构损伤概率PD：

(4)

式中：μD、μID、μI0分别为D、ID、I0的平均值；σD、σID、σI0分别为D、ID、I0的标准差；Φ(σ)为标准正态分布函数。

最后得到结构损伤状态2和3相对于无损伤状态1的损伤概率分别为PD2=87.69%，PD3=94.26%。

由式(4)可见，相比结构状态1：“无损伤”，结构状态2：“2 m长裂缝”对应损伤概率为87.69%，可视为发生了明显的损伤；而结构状态3：“8 m长裂缝”对应损伤概率为94.26%，结构损伤概率在结构状态2的基础上又有明显的增大。结构损伤概率的变化趋势与结构实际裂缝的发生和扩展趋势是定性一致的。

4 结 论

考虑行车激励主要参数的随机变化，建立有限元模型计算随机行车激励下混凝土板梁桥结构在指定控制点的结构加速度响应时程。再对加速度响应时程进行微元分段和频谱分析，进而提取表征结构损伤的指征频率。最后借助概率可靠度方法建立结构损伤性能函数，实现结构损伤概率的量化计算。计算结果与结构损伤状态的发生、发展趋势一致。主要结论有：

1)笔者提出的基于性能函数的结构损伤识别方法是一种非确定性方法，相比传统依靠结构低阶模态频率、振形形状和阻尼等确定性识别手段，笔者方法对动力荷载参数随机性不敏感。

2)笔者方法所需人为设计的动力激励成本为零，不会中断和干扰交通，因而损伤识别结果更为接近桥梁结构在运营状态下的真实状态。

下一步研究中，还需结合具体桥梁体系和形式，对结构损伤概率与结构损伤程度之间的量化对应关系进行深入探讨。此外，必要的室内模型实验和现场实桥检测验证，也是亟待开展的课题。