脉冲输入下基于输入整形法的起重机防摇摆方法

，，

(上海海事大学 航运技术与控制工程交通部重点实验室，上海 201306)

0 引言

随着自动化港口的不断建设和船运业的飞速发展，对于起重机的装卸效率的要求也越来越高。在起重机运送货物的过程中，起重机的加减速，风的阻力和负载自身升降都会让吊重产生摇摆[1]，使货物无法及时到达指定位置，这直接影响了起重机的装卸效率。目前，大部分的吊车由人工操作，负载的摇摆和起重机的运行也由司机手动控制，运输的工作效率依赖司机的操作水平，也与码头自动化的趋势相反。所以为了输送效率的提高及码头作业安全，起重机自动防摇摆控制是十分必要的[2]。解决吊重的防摇摆问题对物流运输行业[3]的发展具有积极的意义[4]。

国内外相关行业和学者已经对防摇控制做了大量的研究，提出了许多方法。按照控制系统的不同进行分类[5]，可将防摇控制方法分为两类：机械式防摇控制法和电子式防摇控制法。其中，电子式防摇控制法又分为开环防摇控制和闭环防摇控制。其区别在于开环[6]控制指控制系统中没用使用反馈环节来控制摆角；闭环控制[7]指控制系统中含有传感器来测量起重机的摆角，通过反馈环节控制吊重摇摆的方法[8]。

闭环控制方法中需要利用传感器采集所需要的信息，例如摆角，加速度等。将数据传送至处理器的控制部分，由电脑进行计算，得出最佳参数后，实时改变速度。然而此方法中的控制系统设计复杂，参数也会受到工业环境的影响，在实时改变速度时会加速小车零件的老化。并且该方法需要的测量传感器成本高昂，在实际应用中不易实现，因此限制了该方法在实际生产中的应用。

对于开环控制方法，以加速度输入的种类不同可以分为阶跃输入法和脉冲输入法。对于阶跃输入法，上海振华集团[9]提出了两段加速的控制方法，假设小车系统为无阻尼的二阶系统，输入二段阶跃，在3T/4时刻系统摆角回到0，其中T为系统的振荡周期。在此基础上，郁春丽[10]研究了阶跃输入下，小车系统为有阻尼的二阶系统，并且提出了该系统二段加速，三段加速，……，n段加速控制方法，其中时间最优解在二段加速下达到，摆角在3T/4时刻回到0。对于脉冲输入法，河南卫华集团[11]的研究是：对于起重机系统，采用黑箱法，不分析其具体的物理特征，以小车的加速度作为输入，摆角作为输出，研究了当输入是二个，三个脉冲时，摆角在T/2，2T/3时刻回到0。

本文将河南卫华集团的二脉冲法、三脉冲法推广为n脉冲法，研究了不同脉冲下的二阶带阻尼系统的防摇控制性能，以便为用户提供更多的防摇方法选择。

1 起重机动态模型分析

考虑到起重机运行中的实际情况，将起重设备中的水平运行的小车，连接负载的绳索和吊重看成一个移动的单摆系统，如图1所示。

图1 起重机吊重系统的动力学原理

对以上模型作如下假设：

假设1：小车和负载看作是有一定质量的质点，且起重机静止不产生相对运动。

假设2：绳索的质量忽略不计，且长度不可拉伸。

假设3：不考虑风力和空气阻力对负载的影响。

根据牛顿运动定律可得：

(1)

(2)

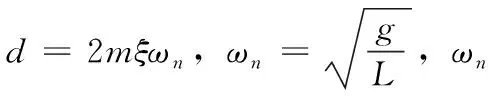
在实际情况下，负载摇摆的角度一般不会超过±10°以内[10]，因此可简化为sinθ≈θ。将式(2)带入式(1)，整理可得：

(3)

(5)

将式(5)进行拉普拉斯变换得：

(6)

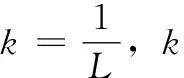
该系统的脉冲响应是：

(7)

2 POSICAST输入整形开环控制方法

O.J.M.Smith教授在50年代提出了POSICAST控制方法，理论的核心是相隔半周期的正弦函数可以相互抵消。输入整形法[12]是一种开环控制方法，其技术是将整形器中的脉冲与初始输入进行卷积计算，将初始输入整形成防摇需要的脉冲，然后控制整个系统。输入整形器[13]实际包含不同个数，不同幅值和时滞的序列。这些参数通过动力学模型得到的脉冲响应组成的超越方程求解获得，通过不同的时间点，给不同幅值的脉冲响应，叠加后的摆角为零。即解下列方程使θ(t)为零：

(8)

其中：ωn为系统固有频率，ξ为系统阻尼比，n为整形器中脉冲的个数，Ai为脉冲响应的幅值，ti为脉冲响应的延迟时间。

3 起重机防摇摆控制方法

本摇摆控制方法的控制原理来自Smith教授的半周期POSICAST方法，即当第一个脉冲输入系统后，延迟半个周期后再输入一个幅值特定的脉冲，去抵消前一个脉冲带来的摆动，在时刻系统的摆角为零。经过进一步的计算发现，脉冲的个数增加时，恰当的选择脉冲的幅值，也可以得到良好的防摇效果。下面给出这些控制方法的详细阐述和理论推导过程

推导过程中涉及到的一些等式如下：

α=ωn*ξ

(9)

(10)

3.1 二脉冲法

理论解释：

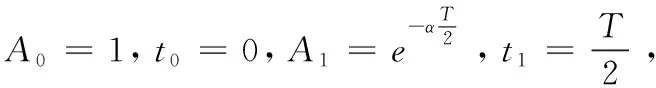
3.2 三脉冲法

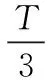
理论解释：

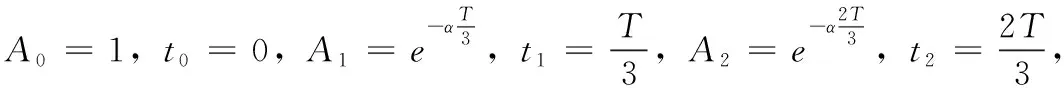
3.3 四脉冲法

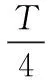
理论解释：

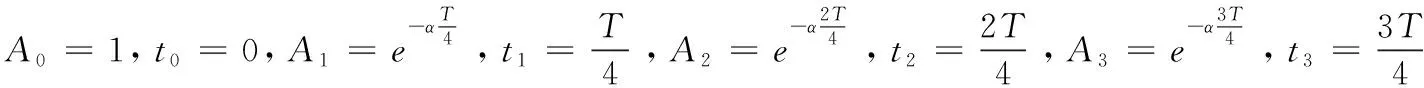
3.4 六脉冲法

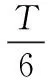
理论解释：

进一步的研究发现，输入任意个数的脉冲，摆角都可以在适当的时刻回到0。

3.5 n脉冲法

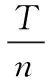
理论解释：

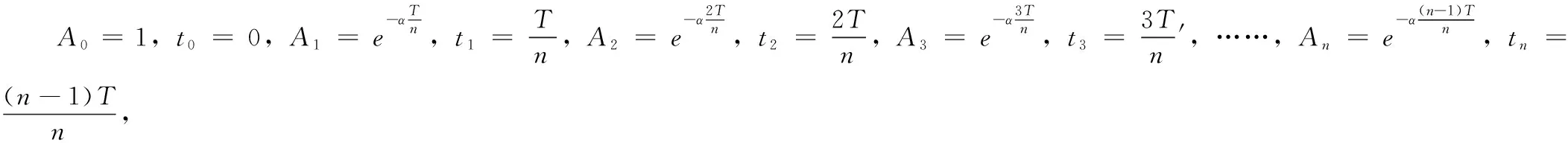
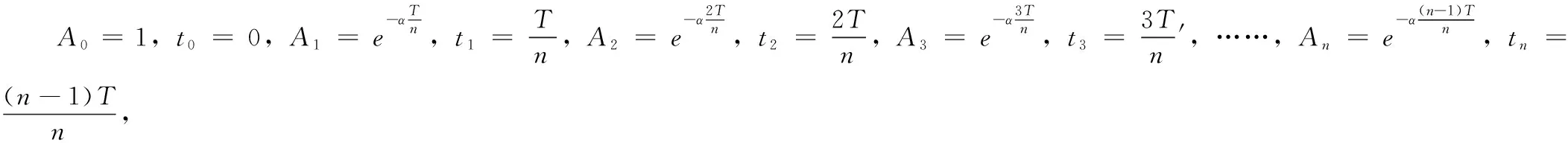
4 基于POSICAST控制方法的仿真验证

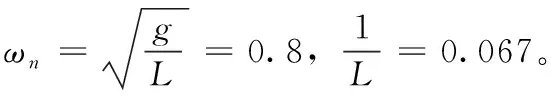
其中:T=7.8 s，α=ωn*ξ=0.0128。

4.1 二脉冲法

该方法中，小车在加速和减速阶段时，负载产生摇摆，在匀速行驶和静止时，负载不产生摇摆。系统的加速度曲线，速度和摆角曲线见图2。本次仿真中，在加速阶段，输入整形器中加速度脉冲的个数为2，脉冲输入的时间间隔相等，脉冲的幅值递减，小车运行中进行两次加速。小车从静止到匀速运动，即从吊重开始摇摆到摆角为零所需时间为3.9 s，等于最后一次脉冲输入的时刻T/2，符合理论计算，运动中小车产生的最大摆角为6.18°。减速阶段小车和吊重的情况与加速阶段一致。

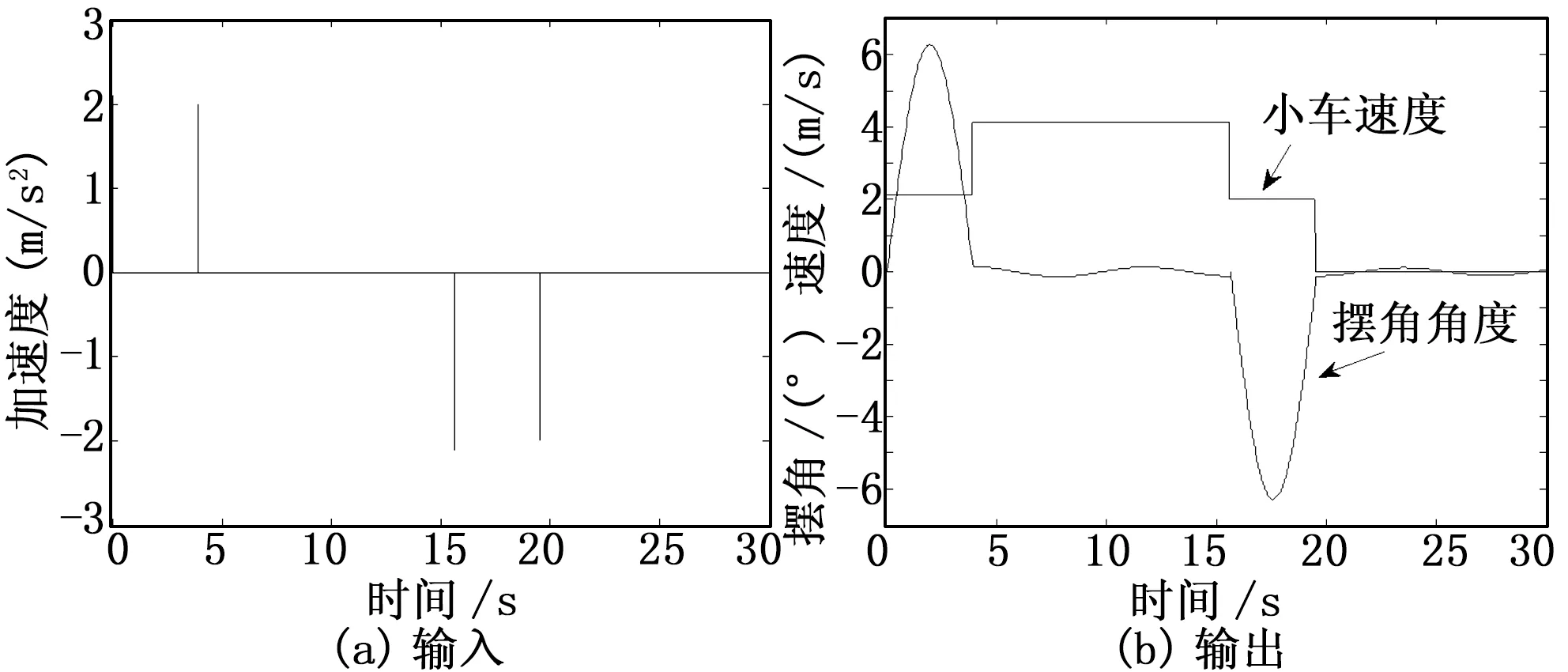
图2 二脉冲法

4.2 三脉冲法

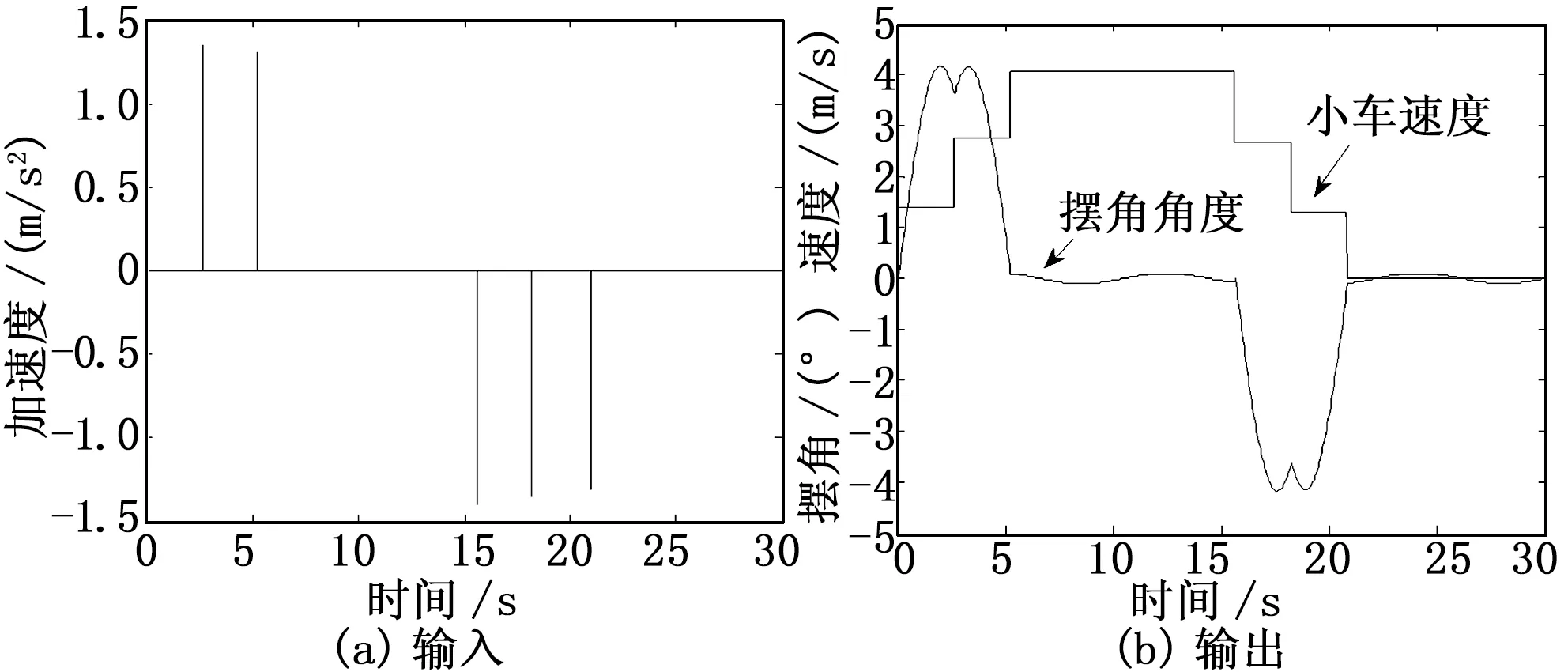
图3 三脉冲法

4.3 四脉冲法

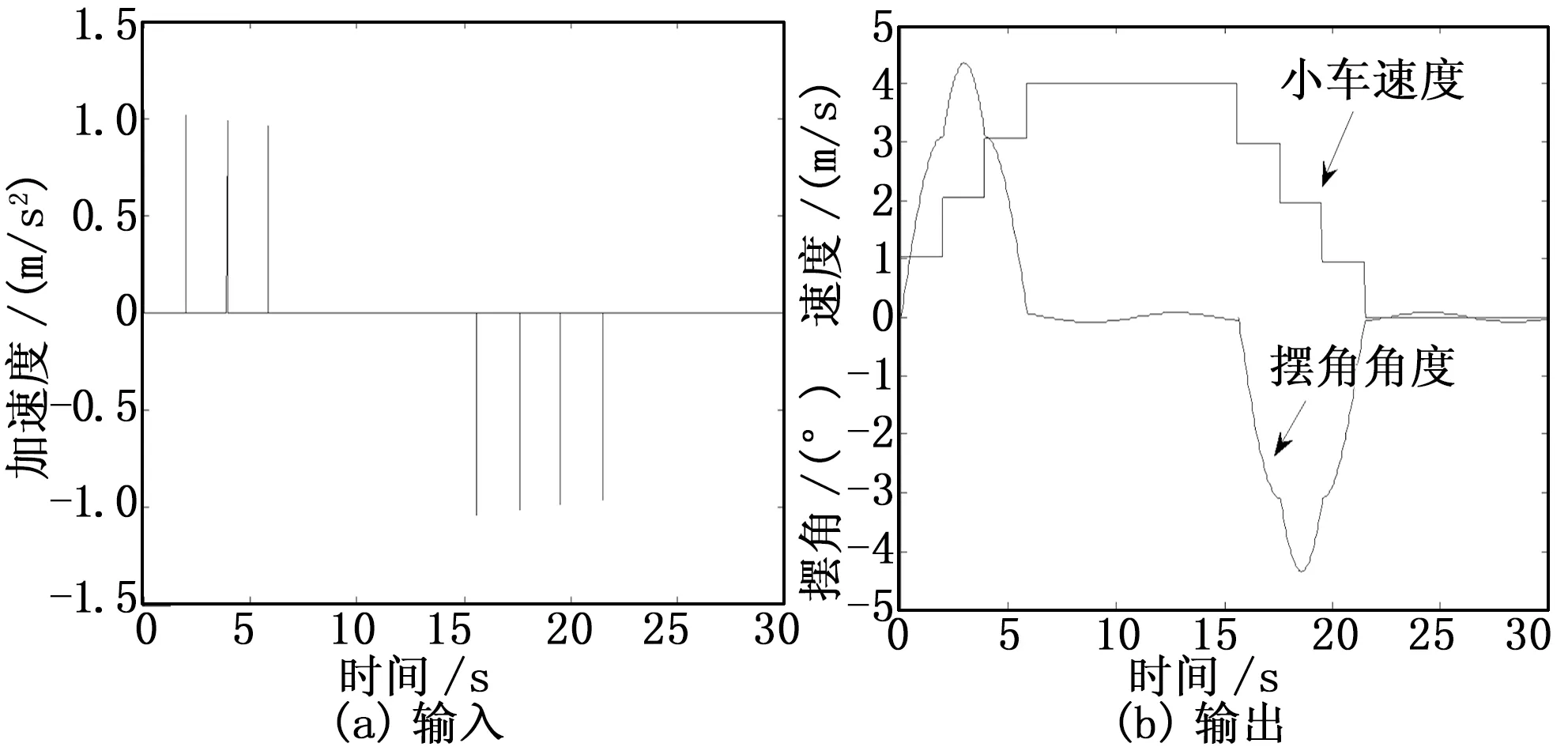
图4 四脉冲法

4.4 五脉冲法

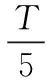
图5 五脉冲法

4.5 六脉冲法

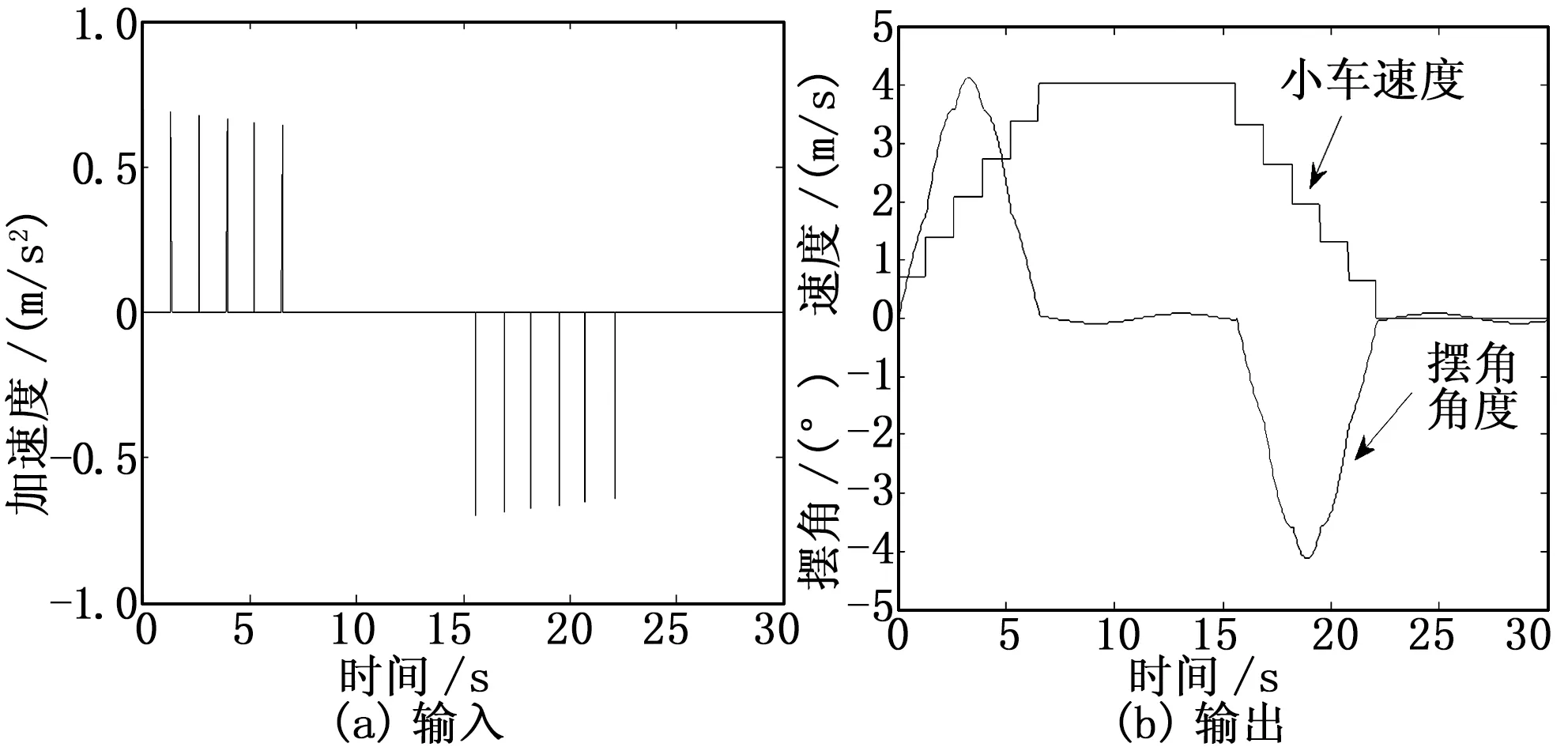
图6 六脉冲法

从以上的仿真可以看出，二脉冲法的摆角回零时间最短，为T/2，但是产生的最大摆角也最大。

4.6 小结

当输入为二脉冲到十脉冲，速度最大值和小车摆角最大值及摆角回零时间见表1。

从表1可以看出二脉冲输入时，负载产生的摆角最大，摆角回到0的时间最短。随着脉冲个数的增加，最大摆角稳定在4°左右，总体的趋势是缓慢减少，而回到摆角的时间渐渐增大，越来越趋近于T。在阶跃输入控制法[10]中最优解是，摆角在3T/4时刻回到0，此时摆角的值最大为7.5°；本方法中的最优解是，摆角回零时间缩短为T/2，此时摆角最大为6°。所以相比于阶跃输入法，脉冲输入法的回零时间减少，最大摆角变小。在实际应用时，可以根据需

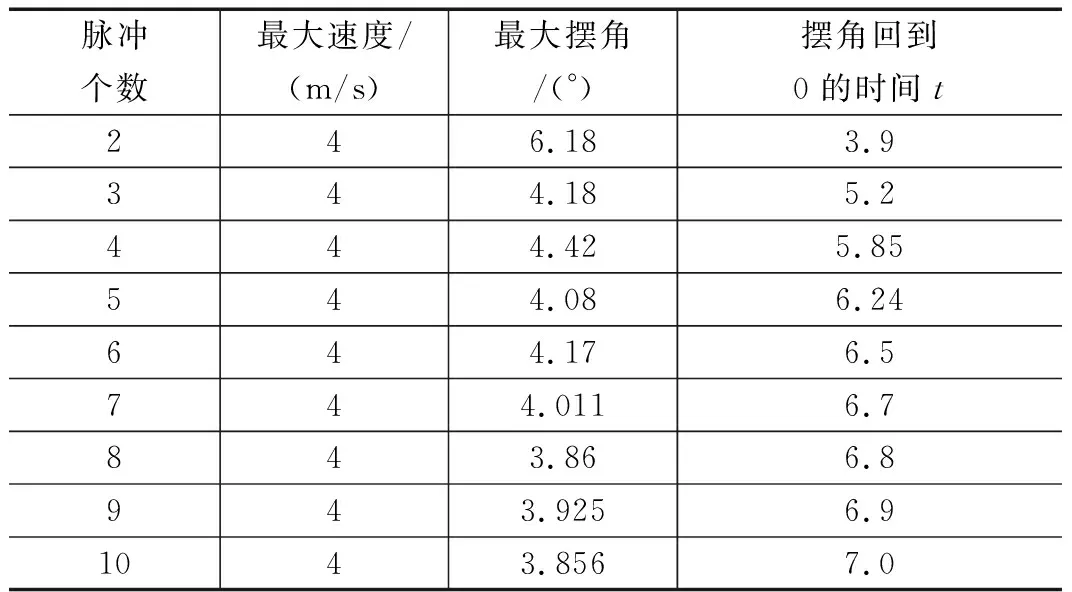
表1 二脉冲法到十脉冲法的防摇特性参数

求和实际情况，选择不同个数的脉冲对应的脉冲输入法，控制摆角在相应时间回到0。

5 总结

本文研究了起重机小车运行时吊重的摇摆问题，通过分析小车的动力模型，分析了加速度与摆角的关系，基于输入整形法，提出了一族脉冲输入下起重机的电子防摇方法。除了理论计算，还在Matlab中进行了仿真验证。仿真结果表明，本方法具有良好的防摇效果。