5G低轨卫星移动通信系统多普勒频偏估计算法

， ，

(中国电子科技集团公司 第五十四研究所，石家庄 050000)

0 引言

随着卫星移动通信系统近些年来的不断发展，军民用户对于新一代的高传输速率、广泛覆盖范围、较低的传输时延以及较强灵活性的5G低轨(LEO)卫星移动通信系统的需求日益增长。相比于地面通信系统，LEO卫星移动通信系统覆盖范围更加广泛，多颗低轨卫星即可实现全球无缝覆盖；而相比于地球同步轨道(GEO)和中轨道(MEO)卫星移动通信系统，LEO卫星移动通信系统又具有较低时延和灵活的网络调度的优点。由于单颗LEO卫星对地面的覆盖范围远小于GEO卫星，需要数十颗甚至数百颗LEO卫星才可以实现全球无缝覆盖。但是低轨卫星由于距离地球较近，信号传输时延得以大大降低，信号功率的衰减也大大降低，较低的卫星信号发射功率即可满足需求，降低了卫星和地面终端的设计成本和复杂度。低轨卫星的传输信号深衰落相比GEO卫星较小，具有更好的性能。而目前低轨卫星移动通信系统的发展已经由话音和短消息向高速宽带业务发展，多媒体宽带通信业务已经成为了下一代低轨卫星移动通信系统的发展需要，这方面具有很大的市场潜力，也是目前卫星移动通信技术研究的一个热点方向。

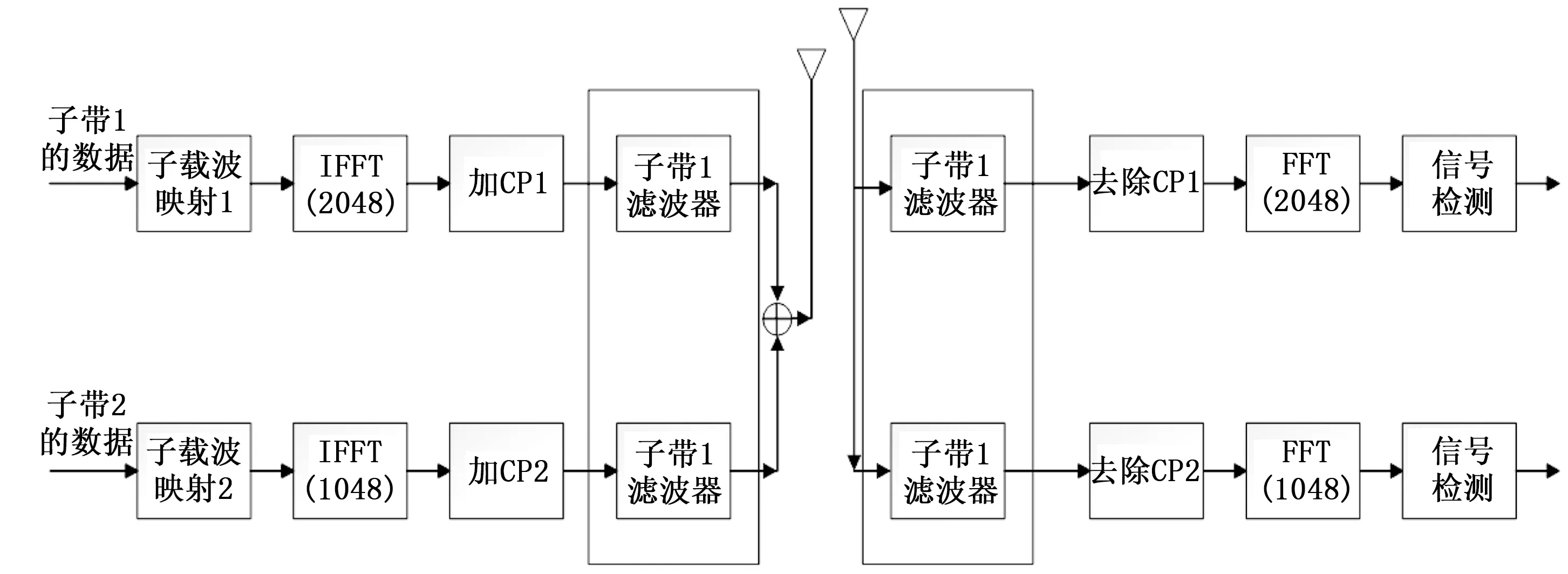
图2 F-OFDM系统框图

而未来的移动通信中，5G的新技术可以满足更加复杂的应用场景和业务，其拥有较高频谱利用率的新型传输技术可以用于新型的5G低轨卫星移动通信系统。其中以华为在OFDM的基础上提出的F-OFDM技术能同时满足下一代卫星要求的高频谱利用率的要求。F-OFDM是一种以OFDM作为基础，将OFDM的子载波划分为若干子带，对其采取滤波来降低带外泄漏的一种新型非正交多载波技术。F-OFDM系统继承了OFDM系统的许多优点，满足了未来5G通信对物理层传输技术的要求。其基本思想是对现有OFDM技术的一种演进，在发送端和接收端将子载波根据需求划分为若干个子带，对每个子带进行滤波操作，使得F-OFDM系统有较高的频谱效率，同时可以灵活应对不同的业务需求。F-OFDM有着比OFDM更低的带外泄露和更高的多用户性能。与其他5G候选波形相比，F-OFDM与OFDM在技术原理上最为接近，最适合完成从4G技术到5G技术的平滑过渡和演进。文献[14]中提出了一种可行的演进方案，在5G实现商用的初期，为了避免大范围更换现有的4G基站等通信设备，将4G网络中作为保护间隔的10%系统带宽使用F-OFDM系统来传输数据。而随着5G技术的进一步推广和4G的逐渐演进，逐步将更多系统资源分配给5G系统中的F-OFDM系统，以此方式逐步完成从4G到5G技术的全面演进，从而将频谱利用率进一步提高。F-OFDM系统本身的前向兼容性和后向兼容性很好，可以和4G技术实现共存，一直到4G技术完成到5G的全面演进[1]。

然而，由于地面移动终端和低轨卫星之间的相对移动速度很大，所以产生了非常大的多普勒频移，低轨卫星移动通信系统的性能受到了严重影响。所以，5G低轨卫星移动通信系统的一项需要解决的重要问题是多普勒频偏的估计和消除。目前对于F-OFDM频偏估计算法的研究文献和资料较少，许多基于OFDM的多普勒频偏估计法应根据F-OFDM的卫星移动通信系统进行进一步研究。

在过去的研究中，多普勒频偏估计方法主要针对OFDM系统设计。文献[2]提出一种利用二阶差分方法来估计多普勒频偏的方法，但这种方法对大多普勒频偏很敏感。文献[3]提出了一种最大似然估计法，估计的精确度很高但是计算复杂度很高。文献[4]提出了一种针对OFDM系统的快速多普勒频偏跟踪补偿法，借助OFDM的循环前缀来实现频偏粗估计，借助子载波导频来实现频偏的精确估计。文献[5]提出了一种最大后验频偏估计法，借助多普勒特性和循环前缀分两步来实现频偏的估计。本文结合了快速多普勒频偏跟踪补偿法和最大后验的估计法，先通过多普勒特性估计整数倍频偏，再借助子载波导频实现频偏的精确估计，计算精度高且复杂度低，与其他现有的频偏估计算法相比具有一定优势。

1 F-OFDM系统模型

在F-OFDM系统中，滤波器处理的对象是每个子载波块，和LTE(Long Term Evolution,长期演进)系统中的资源块(Resource Block，RB)相似。因此，F-OFDM信号的处理是通过资源块作为基本单元实现的。图1是OFDM系统发射端和接收端的框图，图2是F-OFDM系统接收端和发射端框图。

图1 OFDM框图

OFDM符号经过N点IFFT变换以及添加循环前缀(CP)操作后表示为：

(1)

其中：

(2)

Ng是添加的CP的长度，L代表OFDM符号个数，dlm是第l个OFDM符号中映射在序号为m的子载波上的数据，{m′，m+1′,...,m′+M-1}为有效子载波映射范围。

所以，第i个子带的F-OFDM符号可以表示为

xi(n)=si(n)*fi(n),i=1,2...k

(3)

在F-OFDM系统中，发送端对每个子带进行独立的调制和滤波，根据具体的应用环境和场景来灵活分配每个子带的大小。所以子带滤波器的设计也是F-OFDM系统的一个研究重点，必须同时考虑时域特性、频域特性和滤波器实现的复杂度，而其频域特性是子带滤波器设计的最重要问题，需要满足在频域可以实现较好的滤波处理，降低每个子带的带外泄露。同时实现复杂度不能过高，否则F-OFDM将难以在5G中广泛应用。本文F-OFDM系统假设使用理想的低通滤波器进行仿真研究。

si(n)是对第i个子带进行滤波处理之前的数据，fi(n)为第i个子带的滤波器的冲激响应。然后对不同子带产生的数据xi(n)在时域相加之后表示为：

(4)

本文假设信道环境是存在较大多普勒频移的AWGN(加性高斯白噪声)信道，因此，收到的数字信号可以表示为：

r(n)=x(n)*h(n)+z(n)=

(5)

对于低轨卫星移动通信F-OFDM系统，由于会存在较大多普勒频移，各个子载波间会存在严重干扰，系统性能会急剧下降，传输的误比特率提高，必须提出一种适合新传输技术的复杂度低且精确度高的新型频偏估计算法[6-7]。

2 低轨卫星的多普勒特性

LEO卫星在约1000公里高度的圆周轨道以恒定速度围绕地球旋转，在地面位置信息已知的情况下，多普勒频移很容易就可以计算出来。卫星在其轨道任意一点P处的多普勒频移可以由下式分析计算来得出:

(6)

其中:

(7)

rE是地球半径，r是卫星轨道半径，ψ(t)-ψ(t0)]是地球表面沿卫星轨道估计的角距离，θmax表示最大仰角，ωF(t)是卫星的角速度。这里ωF(t)可以近似为一个常数:

ωF=ωs-ωEcos(i)

(8)

这里ωs是卫星运动的平均角速度，ωE是地球旋转的角速度，i是卫星轨道倾角。

假设卫星通信使用S波段的2.4 GHz的频率。通过上两个公式，可以计算出多普勒特性曲线如图3所示。多普勒频移是一个关于卫星移动的角度和最大仰角的函数。可以看出多普勒频移是一个关于时间和最大仰角的S形曲线函数。多普勒特性曲线可以相对地面固定终端的位置得到一个较精确的频移值，但是对于移动终端，其位置的变化会导致其多普勒频移是变化的，多普勒特性便无法再得到一个相对精确的估计值。举例来说，对于低轨卫星移动通信系统，移动终端以0～500公里每小时的速度移动，多普勒特性曲线将会产生1 kHz左右的误差，这将是无法被接受的。因此，新一代F-OFDM低轨卫星移动通信系统需要对多普勒频偏有一个精确的估计值[8]。

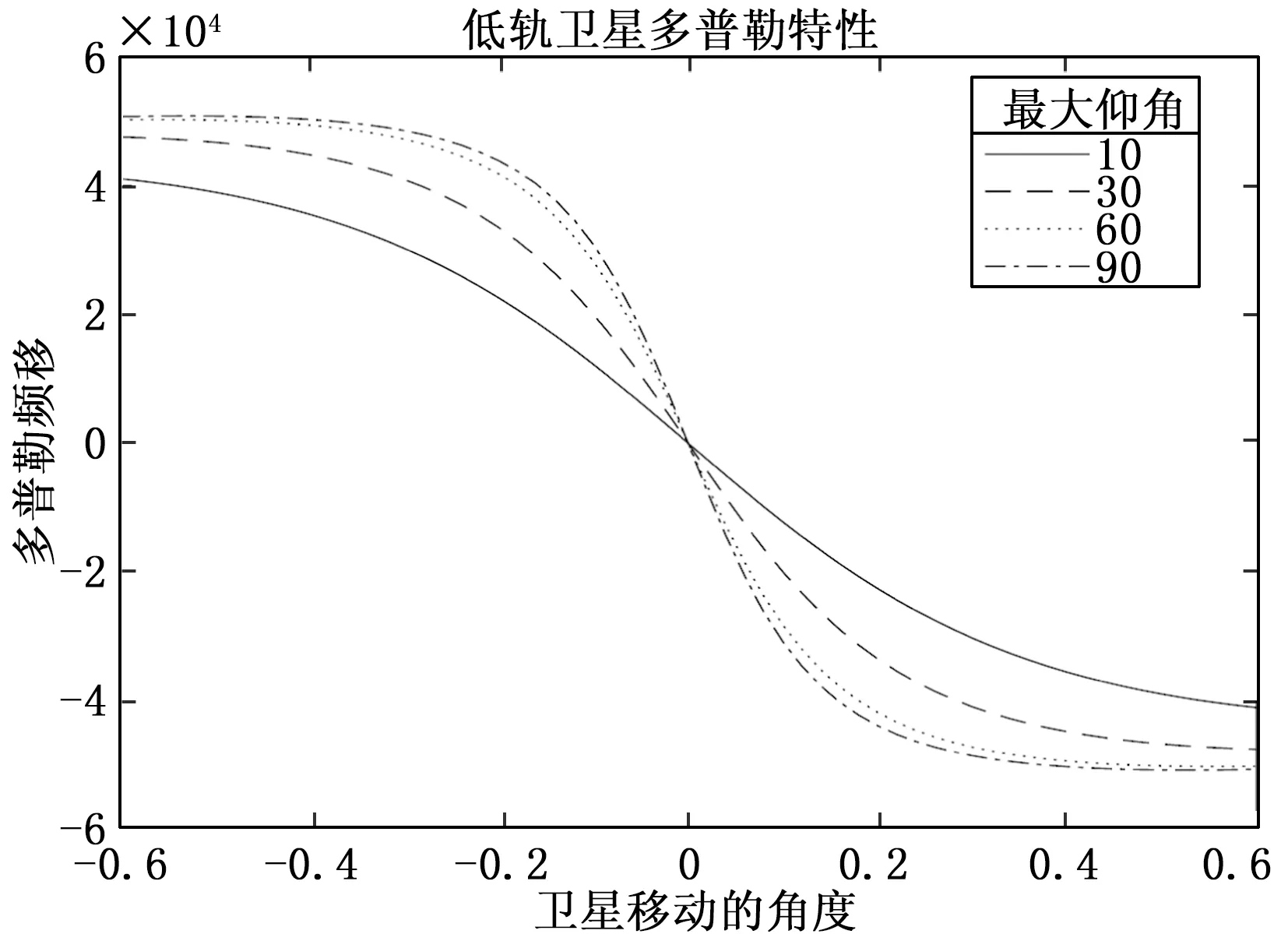
图3 低轨卫星的多普勒特性曲线

3 快速跟踪多普勒频偏估计法

3.1 整数频偏估计

在低轨卫星移动通信系统中，虽然从多普勒特性曲线中估计得到的多普勒频移对于移动终端不够精确，但其误差范围很小(小于1 kHz)，可以被限制在半个载波间隔之内(LTE系统是7.5 kHz)。从多普勒特性中可以得到载波频偏的一个大致范围，如果多普勒特性得出一个估计值67.3 kHz，实际频移可能在66.8～67.8 kHz之间变化，然后归一化频率的变化范围是4.453 3～4.52，则可能的归一化载波频移值是4或5。由此即可从多普勒特性估计出一个整数频偏，可以通过导频估计算法更进一步地估计得出精确的多普勒频偏[9]。

3.2 基于导频的快速跟踪频偏估计算法

导频是在发送端F-OFDM符号一些特定位置的子载波上添加的一些固定数据，文献[10]中提出了利用导频实现频偏粗同步的方法，根据这种方法的思想，可以在F-OFDM系统的一些子载波上添加一些导频符号来实现对多普勒频偏的小数倍估计。

在忽略时间误差和采样时钟误差的条件下，F-OFDM卫星移动通信系统接收机接收的信号可表示为：

yk=xkexp[j(Δθ+θ)]+nk

(9)

其中：Δθ是频偏引起的相位角变化量，而由频偏引起的子载波间干扰被等效为噪声nk。从式中可以看出，多普勒频偏会使接收到的卫星信号产生一个相位旋转ejΔθ，所以基于这一点，可以利用相邻两个F-OFDM符号中的导频相位变化量来估计出小数频偏，即通过求前后两个相邻F-OFDM符号的导频的相关函数来得到多普勒频偏引起的导频的相位变化量[11]：

(10)

然后求平均的导频相位差：

(11)

其中：P是符号中导频位置的集合。由此可得精确频偏为：

(12)

若上述公式中的2个导频符号分别取自第n个F-OFDM符号和第n+D个F-OFDM符号，假设多普勒频偏随时间的变化率较低，此时第n个符号和第n+D个符号之间的频偏可以近似认为是不变的，可以得到精确的小数频估计值为：

(13)

4 系统仿真

分别采用基于循环前缀的最大似然估计的方法和上面所述的基于导频的方法进行频偏估计，使用MTALAB搭建了使用F-OFDM传输技术的低轨卫星移动通信系统，对它们在AWGN信道下的性能进行了仿真。仿真采用的参数为：子载波数N=600，子带数L=12，每个子带50个子载波，每个子带插入一个导频符号，信噪比12 dB，使用QPSK调制，子载波间隔为15 000 Hz。仿真图中，横坐标是加入频偏的真实值，单位是赫兹(Hz)，纵坐标是估计所得频偏的相对于真实频偏的误差。基于循环前缀的最大似然估计频偏的方法的仿真结果如图4所示，基于上面所述的导频子载波估计频偏的方法仿真结果如图5所示。

由下两图可明显看出，与过往OFDM系统经常使用的基于循环前缀的最大似然频偏估计算法相比，上面所述的基于导频子载波的频偏估计方法在1 kHz的频偏范围内都能得到更精确的频偏估计值，再结合第一步中的通过低轨卫星多普勒特性所得到的能精确到1 kHz左右的频偏粗估计值，便可以快速得到低轨卫星和地面终端在某一时刻时的精确的多普勒频偏值。同时在图5中可以看到，子带中插入导频间隔的F-OFDM符号数越小，对时变的频偏的估计精度越高，而频偏随时间变化较缓慢时，可以增大插入导频间隔的F-OFDM符号数，从而提高系统性能。同时在精度满足估计需求条件下，与计算复杂度很高的基于循环前缀的最大似然频偏估计方法相比，基于卫星多普勒特性和导频的快速多普勒频偏估计算法的计算复杂度大大降低。

图4 ML频偏估计算法的估计误差

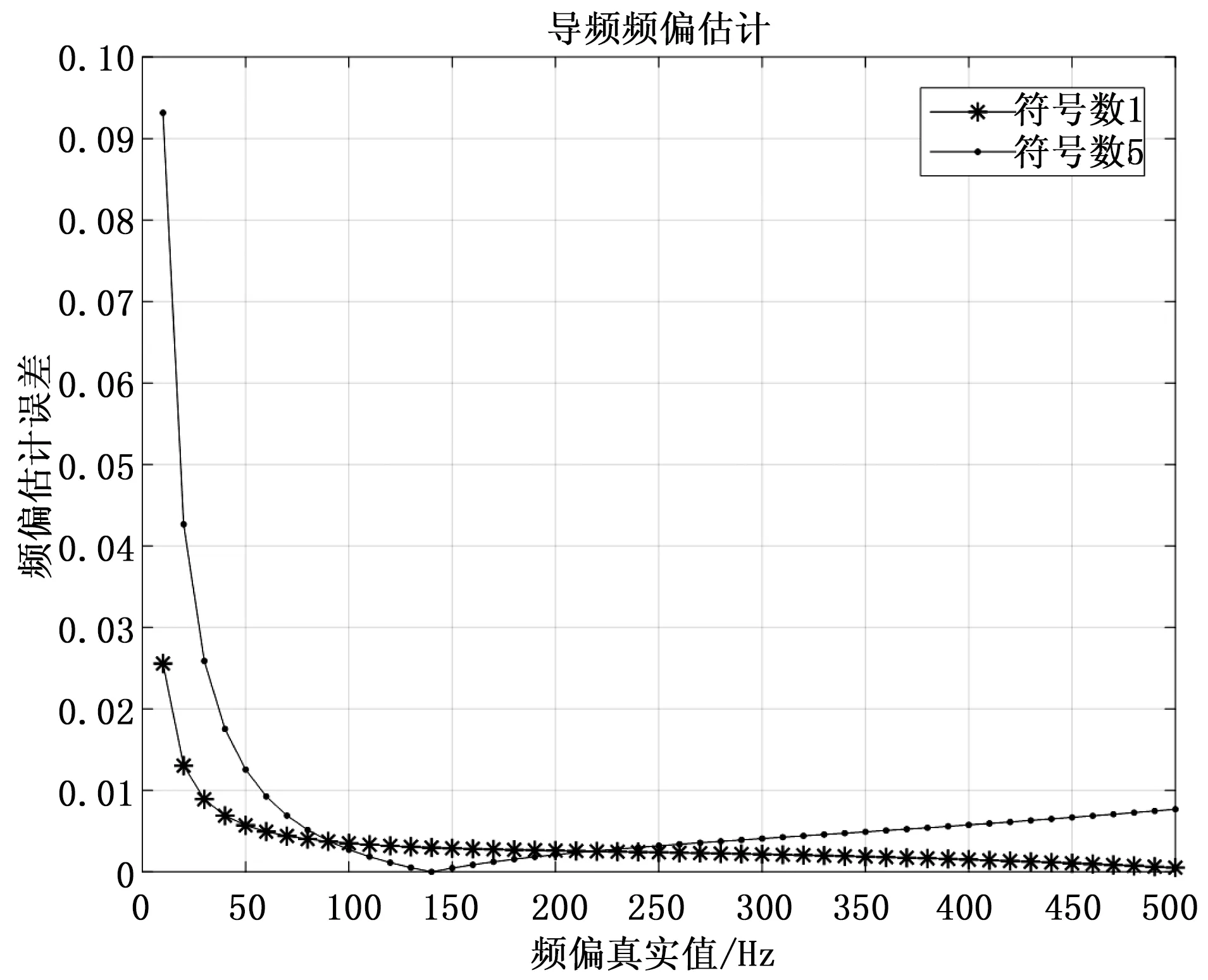
图5 基于导频的频偏估计算法的估计误差

5 结论

为了满足用户终端对移动通信业务的要求，低轨卫星移动通信系统现已成为空天地一体化信息网络系统的重要组成部分。本文结合国内外同类型课题的研究现状，针对当前低轨卫星移动通信系统使用的传输技术的不足，提出了一种采用5G新型F-OFDM传输技术下的低轨卫星移动通信系统，并提出对新型系统的多普勒频偏干扰快速估计的算法。

全文主要完成了F-OFDM系统与卫星移动通信系统相结合的仿真模型在MATLAB下的搭建，以此基础提出了一种新的5G低轨卫星移动通信系统多普勒频偏估计算法。该算法分为两步：第一步，采用低轨卫星多普勒特性对多普勒频偏进行粗估计；第二步，采用导频相关的方法对多普勒频偏进行精估计。通过理论分析、仿真验证了该算法计算复杂度较低，对于低轨卫星多普勒频偏具有较好的估计性能。

与近年来针对低轨卫星多普勒频偏的多种估计算法相比，本算法较使用循环前缀的最大似然法大大降低了计算复杂度，同时提高了精度。与利用循环前缀的二阶差分估计多普勒频率变化率的算法相比，也是具有较低的计算复杂度，同时精度基本相当，与同类型估计算法相比，本算法最大优势在于精度满足估计要求的同时大大降低了计算复杂度。

本文尽管对新一代使用F-OFDM技术的低轨卫星移动通信系统进行了研究，但主要研究重点在与多普勒频偏估计算法，此外仍有许多关键问题需要进一步完善，例如F-OFDM系统给的子带滤波器的设计和波形与多址技术的联合设计等等一系列的关键问题[12-13]。