基于Meyerhof机构的吸力式沉箱基础抗拔承载力极限分析上限解
朱文波 戴国亮 龚维明 赵学亮
(东南大学土木工程学院, 南京 210096)(东南大学混凝土及预应力混凝土结构教育重点实验室, 南京 210096)
吸力式沉箱基础是一种顶端封闭、底部敞开的薄壁圆桶,主要用于海洋平台的基础,其极限抗拔承载力问题是目前研究的热点之一.学者们就竖向荷载作用下圆形基础极限承载力与极限分析上限解进行了大量研究.Chakrahorty等[1]分析了圆形基础地基计算公式系数Nγ和基础宽度B的关系.Clausen[2]基于Hoek-Brown准则研究了圆形基础的地基承载力.Lavasan等[3]、Ornek等[4]针对改良地基研究了圆形基础的地基承载力.胡卫东等[5]基于Meyerhof理论推导了临坡地基极限承载力简化分析方法.张其一等[6-7]在塑性极限分析理论与Meyerhof等效宽度概念的基础上,构造了可变的静力许可应力场,推导了复合加载模式下条形基础承载力的下限解.李亮等[8]根据极限分析中的上限定理,选择合适的机动位移速度场,推导出圆形浅基础受压作用下地基承载力的上限.张国祥等[9]考虑了单元土体所受的侧向土压力对地基极限承载力的影响,推导出理论上更为合理的三维圆形浅基础地基极限承载力上限解.刘拴奇等[10]利用临界滑动场法,计算了浅埋圆形基础的地基承载力,推导出土体条块极限平衡方程.陈飞等[11]构建了圆形基础多块体离散破坏模式,求得竖向极限承载力的上限解表达式.陈中流[12]根据非线性破坏准则,采用多切线法,利用极限分析上限理论对圆形基础地基极限承载力进行了求解.王志云[13]采用典型的Prandtl破坏模式,建立了吸力式沉箱基础抗拔极限承载力的三维极限分析上限解法.由于典型的Prandtl破坏模式为受压破坏模式,吸力式沉箱基础为抗拔破坏,文献[13]中完全采用Prandtl破坏模式不符合吸力式沉箱基础抗拔破坏模式.由上述研究可以看出,关于圆形基础上限解的研究大多以受压分析为主,对吸力式沉箱基础抗拔极限的分析研究较少,关于吸力式沉箱基础采用Meyerhof破坏模式的三维抗拔极限承载力分析未见报道.
吸力式沉箱基础受上拔荷载,基础下土体并非受压破坏,完全采用Meyerhof破坏机构,破坏模式不理想.为了研究吸力式沉箱基础抗拔极限承载力上限解,本文基于Meyerhof破坏机构,选择合适的地基破坏模式及机动位移速度场,推导出理论上更为合理的吸力式沉箱基础极限抗拔承载力上限解.同时,将上限解与文献[14-15]中试验数据进行对比分析,证明了破坏模式的合理性及所提方法的适用性,为吸力式沉箱基础抗拔承载力极限分析提供参考.
1 机动许可速度场的建立
虚功原理表明[16],对于任意一组静力容许的应力场和任意一组机动许可的速度场,外力虚功率等于物体内能消散功率.根据上述原理可推导出上限定理:在所有容许的塑性变形速度场相对应的荷载中,极限荷载最小.根据极限分析上限定理与土体极限平衡理论,对于直径为2R,埋深为L的吸力式沉箱基础,建立如图1所示的机动许可速度场.图中,F为吸力式沉箱基础抗拔承载力上限解;G1,G2,G3分别为圆锥体ABC、对数螺旋线BCDE以及沉箱和筒内土体自重;vp为沉箱上拔速度;v0为BC间断面上速度;v为CDE间断面上速度且速度;φ为土体内摩擦角;θ为v0与v之间夹角;r为对数螺旋线长;r0为对数螺旋线起始长度.假定:①基础底面与地基光滑接触,接触面为最小主应力面;②地基为理想刚塑性体,满足相关流动法则,且不可压缩;③地基破坏区分为2部分,即在轴对称课题所选用的机动场中,锥体ABC为被动破坏区,BCDE对数螺旋线变形区.

图1 失稳破坏模式
吸力式沉箱基础上拔荷载以速度vp向上运动,沉箱基础下锥体ACB随之以速度vp向上做刚体运动.锥体表面ACB为速度间断面.图2为相容速度图.可以推导出v0为
(1)

图2 相容速度图
在对数螺线变形区内,速度v按照指数规律减小,且速度方向总与对数螺线成一角度φ,因此CDE间断面上速度v为
(2)
通过几何关系可以得到
(3)
2 上限分析与能量消散率计算
内能耗散率包括速度间断面上的能量耗散率、变形区能量耗散率以及重力作用下的能量耗散率,外功率为极限荷载作用下的虚功率.间断面单位面积的能量耗散率可以通过黏聚力c与跨层的切向速度变化量v的简单乘积表示.内能耗散率主要有以下几部分组成:①圆锥体ACB区间断面上能量耗散与圆锥体ACB区重力做功功率;②对数螺线CDE变形区内部能量消散率、间断面CDE上能量消散率和BCDE内部重力做功功率;③沉箱外壁与黏附土体界面上的能量耗散率;④筒内土体重力做功功率.
如图1所示,以AC为母线的圆锥间断面ACB上的能量消散率为
(4)
圆锥体ACB区所受重力做功功率为
(5)
式中,γ为地基土重度.
间断面CDE上能量消散率为

(6)
变形区BCDE内部能量消散率为

(7)
变形区BCDE内所受重力做功功率为
(8)
在破坏模式中,沉箱外壁与土体界面上的相对速度分量取基础上拔速度vp.因此,沉箱外壁与黏附土体界面上的能量耗散率为
W4=2πRLacvp
(9)
式中,a为沉箱与土体间的摩擦系数.
在上限极限分析过程中取沉箱与土体的密度相同,其运动方向为以速度vp向上做刚体运动.因此,土塞及沉箱重力做功功率为
WG3=-γvpπR2L
(10)
竖直上拔荷载F的做功功率为
WF=vpF
(11)
根据系统的虚功率方程,竖直抗拔荷载做功功率等于内能耗散功率,从而得到
WF+WG1+WG2+WG3=W1+W2+W3+W4
(12)
则吸力式沉箱基础抗拔承载力上限解F为
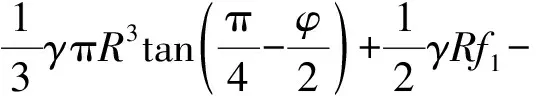

(13)
式中

(14)
(15)
3 计算结果分析
吸力式沉箱基础抗拔极限分析上限解主要由以下2部分组成:①沉箱内土体重和沉箱外壁与黏附土体界面上的能量耗散率提供抗力之和N1;②基础下反向地基承载力N2.这2部分对吸力式沉箱基础的抗拔承载力上限解贡献有所不同.取重度γ=20 kN/m3,沉箱基础半径R=3 m,沉箱与土体界面完全粗糙(a=1),分析2部分承载力与上限解的关系.
由式(13)绘制上限解F,N1,N2与内摩擦角的关系曲线,结果见图3.由图可知,N1随黏聚力增大而增大,不随内摩擦角变化而变化.内摩擦角增大,间断面面积减小,圆锥体ABC、对数螺旋线BCDE体积减小,故上限解F逐渐减小.黏聚力对上限解F影响较大,黏聚力越大,上限解F越大.由图4可知,上限解F,N1,N2分别随着黏聚力的增大而增大.由图5可知,上限解F,N1,N2分别随沉箱半径的增加而增大,且沉箱半径越大,上限解增幅越明显.

(a)c=10 kPa

(b)c=20 kPa

(c)c=30 kPa

(b)φ=20°

(c)φ=30°

图5 上限解与半径关系曲线(c=10 kPa,φ=10°)
表1分析了长径比,c,φ不同时N1,N2提供的承载力与上限解的关系.由表可知,N1不随摩擦角的变化而变化,随黏聚力、长径比的增大而增大,且长径比越大,增幅越明显.反向地基承载力N2约占上限解的40%左右.
为了分析摩擦系数对上限解的影响,以下计算中取沉箱深10 m,半径为3 m,土体重度为20 kN/m3.图6中,a=0表示沉箱与土体界面完全光滑的计算结果,a=1表示沉箱与土体界面完全粗糙计算结果.可见沉箱与土体界面完全光滑上限解小于沉箱与土体界面完全粗糙上限解,且黏聚力越大,摩擦系数对上限解影响越明显.

表1 不同能量耗散区对比分析

(a)φ=10°

(b)c=20 kPa
基于文献[14-15]中的试验数据以及文献[13]中的吸力式沉箱基础抗拔承载力上限解F1,利用Matlab编制相应计算程序,将式(13)计算的上限解F与F1以及试验数据进行对比,结果见表2.表中,F2为试验值.试验数据均采用吸力式沉箱基础快速上拔的极限承载力,式(13)求得的上限解F与试验值F2的误差最大值为28%,最小值为9%.由于反向地基破坏模式选取的不同,本文采用的上限解F小于文献[13]中完全采用Prandtl破坏模式上限解F1,更接近试验值,说明本文中选取的破坏机构较为合理.

表2 计算结果对比分析
4 结论
1)为了研究吸力式沉箱基础竖向上拔荷载作用下承载力上限解,构建出反向Meyerhof破坏机构.引入反向地基承载力,基于Meyerhof破坏机构,将机构下的主动区变为被动区,对数螺旋线方向相反且延伸至沉箱侧壁,建立相应的机动许可速度场,推导出理论上更为合理的吸力式沉箱基础极限抗拔承载力上限解.
2)上限解F随黏聚力增大而增大,随内摩擦角增大而减小.N1随黏聚力增大而增大,不随内摩擦角的变化而变化.上限解F,N1,N2均随着沉箱半径的增加而增大,且沉箱半径越大,上限解增幅越明显.沉箱与土体界面完全光滑上限解小于沉箱与土体界面完全粗糙上限解,且黏聚力越大,摩擦系数对上限解影响越明显.
3)文中上限解与试验值误差最大值为28%,最小为9%.由于反向地基破坏模式选取的不同,本文采用的上限解要小于文献[13]中完全采用Prandtl破坏模式的上限解,更接近试验值.由此说明,本文中选取的破坏机构较为合理,文中采取的上限解是一个更接近极限承载力的上限解.

