运动平台双IMU与视觉组合姿态测量算法*

孙长库,黄 璐,王 鹏,郭肖亭

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)

姿态测量在商业与军事领域都具有重要作用。常见的姿态测量方法包括惯性测量单元IMU(Inertial Measurement Unit)测量[1-2]、视觉测量[3-4]以及磁强计测量[5]。IMU测量速度快,短期精度高,但其误差会随着时间发散,对于低精度MEMS IMU来说误差发散更为明显,一般需要其他测量方法进行不断校正。视觉测量精度较高,稳定性较好,但其采样频率受相机拍摄帧率限制,测量速度较慢,且测量的范围受标记点的限制,当标记点被遮挡时无法实现测量。磁强计测量精度高,但容易受到周围磁场变化影响。

以上几种测量方法各有特点,凭借单一的测量方法实现快速准确的姿态测量难度较大,采用高精度器件来提升精度的话成本会大大提高,因此出现了许多组合姿态测量[6-8]方法,例如IMU与视觉组合测量,IMU与磁强计组合测量等。Hugo[9]研究了一种惯性与视觉组合头部跟踪系统。该方法利用视觉测量对惯性测量校准,在视觉测量周期内惯性独立进行测量,在视觉测量输出结果时将两者测量结果做差,将差值作为下一个周期内的惯性测量的补偿量。其融合方法较为简单直接,其结果依赖于视觉测量的精度。王康友[10]对室内近距离的惯性和视觉组合的定姿技术进行了研究。将相机与IMU固定连接,利用多速率卡尔曼滤波器解决了视觉测量与惯性测量周期的不匹配问题。相较于直接做差补偿,使用卡尔曼滤波器对测量值进行融合[11]更充分利用了视觉和惯性测量结果中的信息。

现有的IMU与视觉组合测量系统中,大多为测量物体相对于惯性坐标系的姿态,例如测量物体相对于地面的姿态。而在实际应用中,有时需将物体放置在特定平台上,测量物体相对于平台的姿态,如机舱中飞行员头部相对于机舱的姿态[12]。当平台处于运动状态时,固定在物体上的IMU的输出包含了平台的运动信息,会对测量结果造成干扰。对此,本文将另一IMU固定在运动平台上,组成双IMU惯性测量系统,通过两运动坐标系之间的欧拉角微分方程计算物体相对于运动平台的姿态。研究了双IMU与视觉组合姿态测量算法,针对IMU与视觉测量结果的融合问题,提出了一种多速率自适应拓展卡尔曼滤波算法来进行融合,将IMU的高速率与视觉的稳定性结合起来,实现了物体相对于运动平台快速准确的姿态测量。

1 双IMU与视觉组合姿态测量原理

双IMU与视觉组合姿态测量系统如图1所示。惯性测量部分,将一IMU固定在转台(被测目标)上,测量转台的运动角速度,设为IMUb;另一IMU通过连接杆固定在运动平台上,测量运动平台的运动角速度,设为IMUn。视觉测量部分,将一带有非共面标记点的立体靶标固定在转台上,相机通过连接杆固定在运动平台上。转台基座固定在运动平台上,设转台与运动平台的初始姿态为零,测量时转台所转动的姿态欧拉角即为被测目标。

图1 双IMU与视觉组合姿态测量系统

设IMUb坐标系为ob-xbybzb,IMUn坐标系为on-xnynzn,方向与IMU各敏感轴相同。目标坐标系为oz-xzyzzz,方向与转台各运动轴相同。平台(参考)坐标系为op-xpypzp,与转台位于原点时的目标坐标系相同。相机坐标系为ov-xvyvzv,z轴与相机光轴重合。惯性坐标系为oi-xiyizi,在空间中固定不动。

1.1 双IMU测量

IMU的角速度原始输出受自身制造工艺、外界温度以及噪声等因素影响,存在一定的误差[13-14]。在读取IMU输出后,减去陀螺仪零偏并采用指数加权平均法进行平滑滤波,减小噪声引起的波动。

(1)

(2)

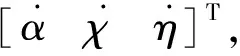
(3)

1.2 视觉测量

视觉测量技术根据所使用相机个数分为单目测量与多目测量,其中单目测量系统结构较简单且视场较大,因此本文采用单目测量方法。利用靶标上的4个非共面红外LED点作为特征点。在得到图像中各特征点的图像坐标以及对应的空间坐标后,采用较为成熟的POSIT[15]算法进行计算求解姿态。

1.3 多速率自适应拓展卡尔曼滤波算法

得到双IMU与视觉测量的结果后,采用多速率自适应拓展卡尔曼滤波(MAEKF)算法进行融合。与传统的EKF相比,使用衰减记忆[16]自适应算法对滤波器是否发散进行了判断,若发散则增大融合过程中视觉测量的权重,使滤波器更好地克服发散问题,获得更好的融合效果。

设系统的状态模型方程和测量模型方程为:

(4)

(5)

测量时IMU与视觉更新频率不同,视觉测量频率较低,IMU则频率较高。将IMU测量频率设为视觉测量频率的整数倍,采用多速率滤波器融合不同频率的数据。当视觉测量无输出时,只进行惯性计算以及卡尔曼滤波估计误差方差阵P的迭代,输出值为惯性测量值,当视觉输出数据时再进行数据融合,输出值为融合测量值。多速率滤波器的输出如式(6)所示:

(6)

普通的卡尔曼滤波器在滤波时对于滤波收敛问题考虑较少,当滤波器参数以及初始值选择(R、Q、P0)不合适时,有时会导致滤波发散,使滤波偏离真值。引入评判滤波发散的标准可以为改善滤波器性能提供依据。将衰减记忆算法与卡尔曼滤波结合,在预测误差方差阵中引入遗忘因子S。引入的遗忘因子S相较于传统的加权衰减记忆滤波,其取值由残差序列与其协方差阵决定,并引入滤波发散判断机制,对卡尔曼滤波的发散起到更好的收敛效果。

当视觉测量输出结果时,残差序列:

(7)

为白噪声序列,其协方差阵为:

(8)

将残差序列平方和与协方差阵的迹的比较作为滤波发散判据:

(9)

γ≥1,为发散系数。γ的大小决定了发散判断的严格程度,当γ=1时为严格发散判断。若式(9)不成立则系统收敛,S=1,此时式(5)为普通的卡尔曼滤波方程,若式(9)成立则系统发散,需要对遗忘因子S进行估计。利用严格发散判据进行估计,此时:

(10)

(11)

整个卡尔曼滤波系统可分为三大部分:增益计算部分、测量更新部分与衰减记忆遗忘因子计算部分。增益部分中,根据IMU的角速度输出值以及前一刻的姿态计算卡尔曼滤波器的增益矩阵、预测误差方差阵与估计误差方差阵。测量更新部分中,通过判断IMU与视觉测量的计算时间是否相等来决定姿态更新输出为惯性测量值还是融合测量值。遗忘因子部分中,根据残差序列与其协方差阵比较来判断滤波器是否发散,从而更新S值。系统的流程如图2所示。

图2 多速率自适应拓展卡尔曼滤波流程图

2 惯性测量坐标系之间的标定

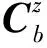
2.1 标定矩阵

IMUb与转台之间刚性连接,采用基于TRIAD[17]算法的正交双矢量标定法进行标定。正交化双矢量标定法在矢量选择上使用两个相互正交的矢量,与TRIAD算法相比少了一步叉积使矢量正交的步骤。

(12)

组合移项得:

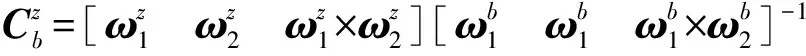
(13)

2.2 标定矩阵

(14)

(15)

ai为矢量的权重,设ai=1/n,得

(16)

g(q)=qTKq

(17)

(18)

式中:Z=[B23-B32,B31-B13,B12-B21]T,S=B+BT,s=trB。K的最大特征值λmax所对应的特征向量即最优四元数qopt。

Kqopt=λmaxqopt

(19)

3 实验与结果分析

搭建如图3所示的运动平台双IMU与视觉组合测量系统。

图3 实验装置

图4 测量靶标的结构

图5 不同测量方法的输出频率对比

图5中组合测量的输出由两种颜色的点组成,其中绿点为此刻组合测量的姿态输出值由惯性测量部分决定,黑点为此刻时组合测量的姿态输出值由滤波融合的结果决定,黑点与视觉测量输出时间相同,即当视觉存在输出时组合测量的输出为滤波融合值。

3.1 标定实验

在测量开始前需要进行坐标系标定。标定矩阵时,运动平台静止,转台分别绕x轴与z轴以1 °/s的速度匀速运动30 s。此时IMUb各轴的输出如图6 所示。

图6 转台运动时IMUb各轴输出

标定矩阵时,转台静止于原点,令运动平台随机摆动。IMUb与IMUn的输出如图7所示。

图7 摇摆台任意运动时IMU各轴输出

各标定矩阵计算结果如表1所示。

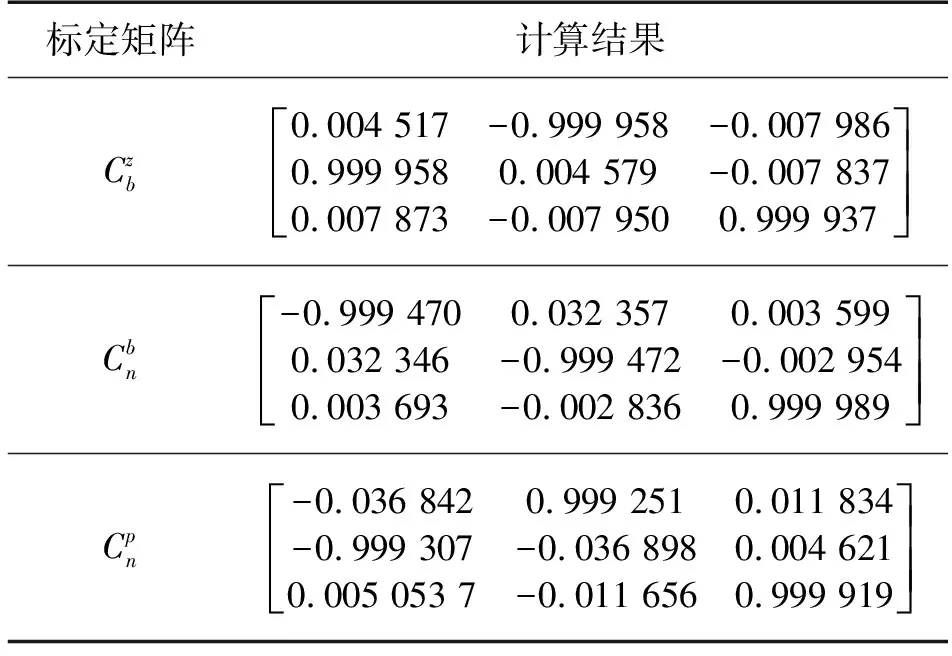
表1 标定矩阵计算结果

3.2 单轴运动实验

令转台绕转台坐标系的x轴以1°/s的速度匀速往返转动,最大角度为60°,从t=0时刻起开始测量。卡尔曼滤波器的初始化参数为:

以t从1.74 s到1.75 s时多速率自适应拓展卡尔曼滤波的的更新为例,分析滤波过程中各个变量的更新情况。

t=1.74 s时,视觉无输出,惯性部分独立进行测量,增益计算部分计算卡尔曼滤波器的增益矩阵K、预测误差方差阵Pk,k-1与估计误差方差阵Pk,此时测量更新部分的输出为惯性测量值,衰减记忆遗忘因子计算部分无更新。各项结果如表2所示。

t=1.75 s时,增益计算部分与t=1.74 s时相同,视觉有输出,测量更新部分输出融合测量值。遗忘因子部分根据滤波是否发散来更新S值,t=1.75 s时式(9)成立,根据式(11)更新S,各项结果如表3所示。

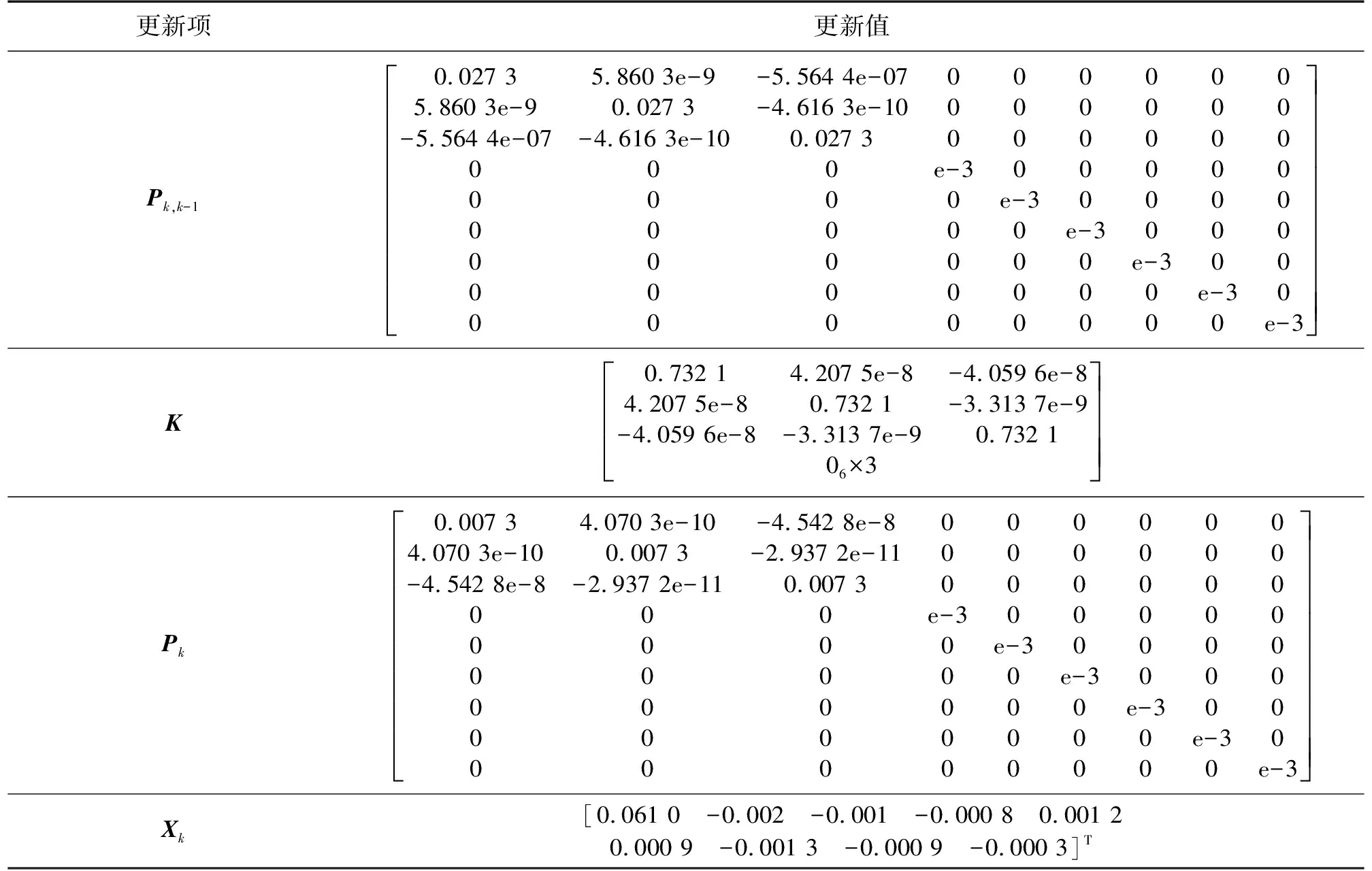
表2 t=1.74 s时各项输出

表3 t=1.75 s时各项输出

t=1.76 s时,视觉无输出,与t=1.74 s时的计算相同,惯性部分独立进行测量。以此类推,直到t=2.0 s 时视觉再次有输出,与t=1.75 s时的计算相同。整个测量过程中S值的变化如图8所示,当滤波发散即式(9)成立时,根据式(11)更新S,其余时刻S=1。

图8 S值变化

得到惯性、视觉单独进行测量的测量值以及组合测量值,以转台自身输出的角度作为真值对测量值进行误差计算。如式(20)所示:

(20)

图9 单轴转动测量结果

图9中蓝线为惯性测量结果,红线为视觉测量结果,绿线为组合测量结果。由测量结果得知:惯性测量的姿态角误差随着时间发散,120 s后误差达到3°以上,组合测量则很好的控制了滤波的发散,姿态角的输出与视觉测量接近,并且更新频率与惯性测量相同,保持较高频率输出。

当转台运动到57°到60°和-50°到-60°的范围时,靶标在相机的视场之外,此时视觉无法进行测量,无姿态输出,图10(c)即部分特征点在相机视场外时所采集的图像。此时惯性部分独立进行测量,组合测量的输出由惯性部分决定,图9(a)中红圈部分的测量结果放大后如图9(b)所示。由图可知,在视觉测量失效的短时间内组合测量能较好地跟踪转台的姿态变化,误差发散在可接受范围,可以认为系统正常工作。因此,组合测量与单独的视觉测量相比,不仅提高了测量速度,还扩大了测量范围。

图10 测量过程中相机采集的部分图片

3.3 多轴运动实验

令转台以2°/s的速度绕x、z轴交错往返转动,具体运动轨迹为:x轴正向旋转30°→z轴正向旋转30°→x轴负向旋转60°→z轴负向旋转60°→x轴正向旋转30°→z轴正向旋转30°。测量误差计算方式与3.2相同,测量结果如图11所示。

测量结果误差的均方根误差(RMSE)的计算如式(21)所示,均方根误差与误差绝对值的最大值如表4所示。

(21)

图11 多轴转动测量结果

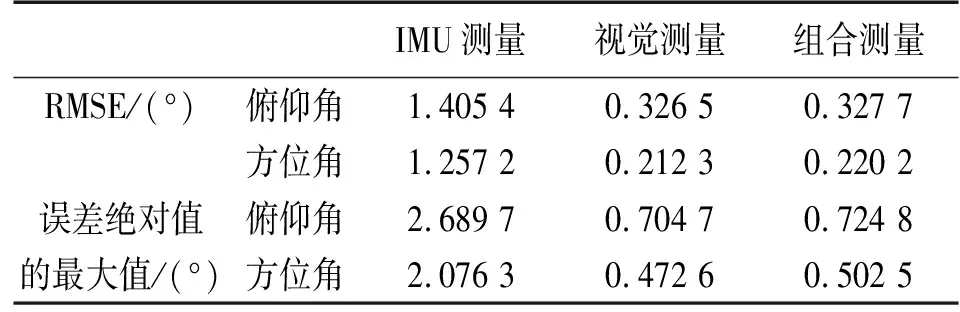
IMU测量视觉测量组合测量RMSE/(°)俯仰角1.405 40.326 50.327 7方位角1.257 20.212 30.220 2误差绝对值俯仰角2.689 70.704 70.724 8的最大值/(°)方位角2.076 30.472 60.502 5

由图11和表4得知:在多轴运动的情况下的测量结果与单轴运动类似,组合测量结果的准确度优于IMU测量,与视觉测量接近,测量频率与IMU测量相同,远高于视觉测量。在整个运动过程中组合测量误差的姿态角均方差在0.35°以内,证明了系统在测量运动复杂的被测目标时也能保持一定的稳定性与精度。

4 结论

本文研究了运动平台上双IMU与视觉组合姿态测量算法。利用固定在平台上的IMUn补偿平台运动对姿态测量的影响,通过欧拉角微分方程计算相对姿态,并采用正交双矢量标定法与q-method标定惯性测量中的转换矩阵。视觉测量采用POSIT算法计算姿态。提出了一种多速率自适应拓展卡尔曼滤波算法,用于融合IMU与视觉的测量结果。搭建了双IMU与视觉组合姿态测量系统并进行了实验论证。实验证明,组合姿态测量算法实现了快速高精度的姿态测量。相较于惯性测量,组合测量抑制了误差发散,可保持长时间稳定工作;相较于视觉测量,组合测量提高了计算速度并增大了测量范围。在多轴运动的情况下,组合测量的姿态角均方差在0.35°以内。