基于学习机的WSNs栅栏覆盖构建算法*

刘绍刚

(滇西科技师范学院信息工程学院,云南 临沧 677000)

无线传感网络WSNs(Wireless Sensor Networks)已广泛应用于多类领域。而栅栏覆盖(Barrier Coverage)是应用于边界监测或战场勘察的一种覆盖模型[1]。所谓栅栏覆盖是指将传感节点部署于狭长的带状区域,并由传感节点对移动目标进行检测的技术。例如,在边境监测应用中,利用栅栏覆盖检测非法入境者[2];在林业保护应用中,利用栅栏覆盖,可检测火势蔓延数据。

与点覆盖、区域覆盖等传统覆盖不同,栅栏覆盖是部署于狭长区域,并不需要传感节点覆盖整个部署区域[3],但需要由多个传感节点协作形成横穿部署区域的栅栏,如图1所示。在L×W的狭长部署区域(L>W)内,存在三条栅栏,它们横穿整个部署区域[4]。

图1 栅栏覆盖示例

每条横穿部署区域的栅栏也称为穿越路径CP(Crossing Path)。穿越路径是一条由多个节点协作构成的路径,且横穿区域。因此,如何构建CP是栅栏覆盖的基础。此外,由于WSNs中传感节点属于微型设备,存在能量受限问题。一旦节点能量耗尽,就形成覆盖空洞区域。因此,构建CP就是以最小的传感节点数构建成横穿部署区域的栅栏。节点数越小,能耗也就越小,覆盖时间也就越长。

目前,国内外研究人员对栅栏覆盖问题进行了不少的研究。在国外,文献[5]采用休眠/唤醒机制处理栅栏覆盖问题,通过休眠/唤醒机制扩延网络寿命和目标检测质量。而文献[6]研究了二维和三维WSNs区域的栅栏覆盖问题,并推导的分布式算法,证实了可形成最优节点集覆盖边界。同时引用自修复算法。此外,文献[7]引用拉格朗日松弛技术分析了栅栏覆盖的成本问题,并提出两类启发式算法解决栅栏覆盖问题。

而国内研究学者对栅栏覆盖问题也进行了较深入研究。例如,文献[4]提出分区强的k-栅栏覆盖算法。将检测区划分多算法子区,并引用匈牙利算法优化覆盖集。但是此算法并没有关注算法的能效问题,类似地,文献[8]提出概率栅栏覆盖算法,并利用虚拟半径确定形成概率栅栏的目标位置。而文献[1]提出基于粒子群的有向传感网络的栅栏覆盖增强算法,其将多维求解问题转化一维,降低了算法复杂度。然而该算法是针对有向传感网络。

为此,考虑到栅栏覆盖的复杂性以及学习机的特性,提出基于学习机的栅栏覆盖算法BCLA(Barrier Coverage based on Learning Automata)。BCLA算法利用学习机建立节点动作概率矢量,并选择具有最大概率的节点构建栅栏。实验数据表明,提出的BCLA算法在限定节点数的条件下,增加了构建的栅栏数。

图2 不同节点的感测和通信示意图

1 约束条件

假定N个节点随机分布于L×W的部署区域A。节点的感测半径、通信半径分别为Rs、Cs,且感测范围和通信范围均为圆形,如图2所示。不失一般性,假定Cs≥2Rs。

引用二值感测模型BSM(Binary Sensing Model)[9]。如果目标位于节点si的感测范围内,则节点si检测该目标的概率为1,否则为零,如式(1)所示:

(1)

式中:d(si,P)表示节点si(xi,yi)与目标P(x,y)间欧式距离,其定义如式(2)所示:

(2)

引用图论(Coverage Graph,CG)表示网络拓扑结构。令G=(V,E),其中V为顶点(节点)集,且V={s1,s2,…,s|V|}。而E为边集,且E={e1,e2,…,e|E|},其中|V|、|E|分别表示顶点数、边数。此外,考虑两个虚拟的传感节点,其分别在网络的左、右边界,并将它们分别称为源节点S和目的节点T。如图3所示,图3显示了两条穿越路径的网络,左、右两边分别为虚拟的源节点和目的节点。所谓穿越路径CP(Crossing Path)是横穿整个部署区域的路线,入侵者若想窜入区域,至少被该路线的某一个节点发现。

然而,为了加强对部署区域的防护,增强栅栏覆盖性能,在部署区域仅构建一条CP是不够的,通常部署k条CP,这也称为k-栅栏覆盖。在k-栅栏覆盖中,当入侵者窜入部署区域,至少被位于不同CP的k个传感节点所感知。图3显示了2-栅栏覆盖(k=2)情况。

本文需要解决的问题就是如何构建CP,进而实现k-栅栏覆盖。

图3 k-栅栏覆盖(k=2)

2 学习机概述

学习自动机LA(Learning Automata)是利用与环境不断的交互,调整自己行为的学习算法。即依据环境条件,从可选的动作集中选择最优的动作。所谓最优动作是指能得到环境奖励概率最大的动作。此外,本文引用的主要变量标识如表1所示。

表1 变量标识符

LA属迭代算法,其目的在于从动作集中选择最优的动作[10]。LA与环境相互作者的示意图如图4所示。

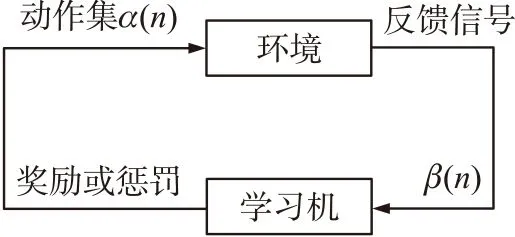
图4 LA工作模型

利用组E={α,β,c}描述环境,其中α={α1,α2,…,αr}为有限动作集,而β={β1,β2,…,βr}为输出集,其受环境加强信号控制。c={c1,c2,…,cr}为惩罚概率集,且c中每一个元素ci与动作集α中的αi一一对应。

而本文引用文献[11]的变量-结构学习机。因此,可利用式(3)表述学习过程:

p(n+1)=T[p(n),α(n),β(n)]

(3)

式中:T为学习函数。而p(n+1)、p(n)分别表示在第n+1、n轮的选择动作α(n)的概率。

令α(k)表示LA在第k轮所选择的动作,而p(k)表示选择此动作集的概率。当环境给出的是增强信号,即惩罚因子β(n)=0,就依据式(4)对概率p值进行更新:

(4)

若给出的减弱信号(需进行惩罚),对依据式(5)对概率p值进行更新:

(5)

式中:pi(n)、pj(n)分别表示选择动作i、j的概率。而r是动作集数。而式(4)和(5)中的a和b分别表示奖励和惩罚因子。

3 BCLA算法

BCLA算法主要由初始阶段、学习阶段和监测阶段组成,其中监测阶段用于构建栅栏。

3.1 初始阶段

最初,每个节点广播通告消息,其包含节点位置和ID号。一旦接收来自邻居节点发送的通告消息,节点就将此发送节点作为邻居节点,并记录此节点的ID。假定节点si收到了M条通告消息,则节点si共有M个邻居节点,且用Ni={s1,…,sM}表示节点si的邻居集。

图5 网络拓扑示例

值得注意的是,这是动作概率的初始值。在学习阶段,会通过对环境的学习,更新动作概率值。

3.2 学习阶段

学习阶段完成对动作概率值的更新。首先,源节点先依据动作概率矢量P选择下一跳节点。选择原则:从P中选择最大动作概率加入CP,用ψCP表示已加入CP的节点集,最初ψCP=φ。如果动作概率相同,则首先将比自己横坐标小的节点的动作暂停(不选择),然后,再从剩余的动作集中随机选择[13]。由于栅栏覆盖是在狭长区域,则可以只利用横坐标信息选择节点。

仍以图5为例,节点4共有5个动作(5个邻居节点),且初始动作概率均为0.2,即P4={0.2,0.2,0.2,0.2,0.2}。而节点1、2、5的横坐标均小于节点4的横坐标。因此,节点4只可能从6、7这两个节点中随机选择一个节点。

一旦选定了节点,就向其发送动作消息A_Mes。接收到A_Mes消息,则先计算将自己加入CP后,ψCP内所有节点的平均剩余能量。具体而言,节点si向节点sj发送了A_Mes消息,则节点sj先计算自己和ψCP内所有节点的剩余能量的均值Eave:

(6)

如果Eave大于Emin,且|ψCP|+1小于Cmin,即满足式(7),则节点sj向就节点si奖励R_Mes消息:

(7)

式中:Emin、Cmin为系统参数,且分别表示最已选节点的最小剩余能量、已选节点的最少节点数。

一旦收到R_Mes消息,节点si就对节点sj的所对应的概率值进行奖励[14]。相应地,对其他动作集进行惩罚,即依据式(4)进行更新概率矢量。因此,节点sj的动作概率值就被增加,相比之下,其他动作集的概率值就减少了。

若不满足式(7),则就发送惩罚消息P_Mes消息。一旦收到P_Mes消息,节点si就式(5)更新概率,即对节点sj惩罚,相比之下,就是对其他动作集进行嘉奖,它们的概率值就增加了。以节点si和节点sj为例,上述过程如图6所示。

图6 动作概率更新过程示例

从上述过程可知,BCLA算法通过学习自动机选择最优节点构建CP,具体而言。节点依据自己邻居节点数,计算初始动作概率矢量,然后再计算反馈信号,即利用式(6)计算剩余能量,然后再利用学习机,进行惩罚或奖励,即利用式(7)判断。最终对动作概率矢量进行更新。对应图4,可得出图7,其显示了BCLA算法如何利用学习机选择节点。

图7 基于LA的BCLA算法

3.3 构建CP阶段

完成了学习阶段后,每个节点已保存了动作概率矢量。因此,每个节点就选择具有最大动作集的节点作为CP的下一个节点。然后,向使已选择的节点发送活动状态消息Act_Mes,一旦接收了该消息,节点就保持活动状态,而其他未被选中的节点处于休眠状态,这有利于保存能量,提高能量效率。换而言之,构建CP过程,就是激活节点状态的过程。只有在CP内的节点,才保持活动状态。图8显示了节点活动状态过程。

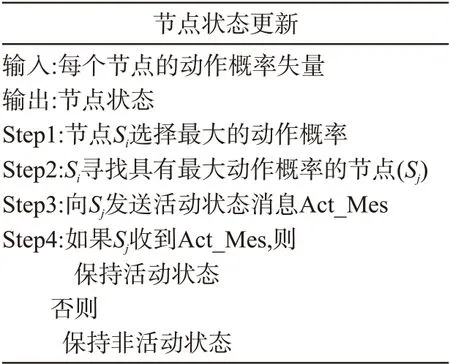
图8 节点活动状态流程

4 性能仿真

为了更好地分析BCLA算法的性能,利用NS-2.34软件建立仿真平台[15]。N个传感节点分布于200 m×150 m部署区域内。仿真参数如表2所示。

表2 仿真参数

同时,选择文献[16]的不相交路径DPA(Disjoint Path Algorithm)和文献[17]所提出的最大强栅栏算法MSBA(Maximizing Strong Barriers Algorithm)算法作为参照,并分析它们所建立的栅栏数的性能。在同等条件下,栅栏数越多,性能越好。此外,考虑到数据的随机性,每次实验独立重复30次,取平均值作为最终的实验数据。

图9 节点数对栅栏数的变化

4.1 实验1

本次实验分析节点数N对栅栏数的影响,其中实验条件:节点的感测半径Rs=30,N从100至400变化,且步长为50,实验数据如图9所示。

从图9可知,节点数N的增加,增加了栅栏数。这与预期的相吻合:节点数越多,可选择加入穿越路径的节点了就越多。与DPA、MSBA算法相比,BCLA算法的能够建立更多的栅栏数。例如,当N=400时,BCLA算法的栅栏数比DPA算法提高了近65%。而与MSBA算法相比,提出的BCLA算法的所建立的栅栏数平均提高了8%。这主要是因为MSBA算法是利用EdmondsKarp算法[18]建立栅栏数,而BCLA算法采用分布式算法,且每个节点利用LA进行学习,实现了以最少的节点数构建一条CP。

4.2 实验2

本次实验分析节点的感测半径Rs对栅栏数的影响,其中实验条件:节点数N=300,Rs从15至40变化,步长为5,实验数据如图10所示。

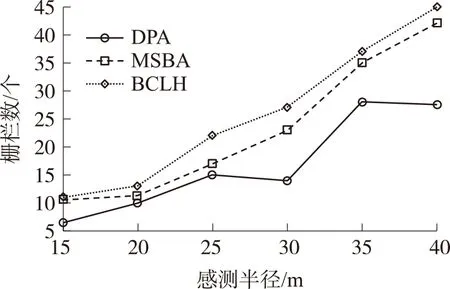
图10 感测半径Rs对栅栏数的影响

从图10可知,感测半径Rs的增加,有利于栅栏数的建立,原因在于:感测半径越大,构建一条CP的所需节点数也就越少。在总的节点数不变的情况下,就能够建立更多的栅栏数。与DPA和MSBA算法相比,提出的BCLA算法的栅栏数得到提高。当Rs=40时,BCLA算法的栅栏数比DPA提高了近63%。

从上述的仿真数据可知,提出BCLA能够以最少的节点数构建栅栏数,原因在于:BCLA算法充分利用了学习机对环境的自适应能力,能够应对环境变化,进而优化了栅栏数。

4.3 实验3

本次实验分析算法的复杂度,并选择时间复杂度指标反映算法的复杂度。假定BCLA算法中部署的节点数为N、边数为E。BCLA算法、DPA和MSBA算法的时间复杂度如表3所示,其中K表示在学习阶段的迭代次数,V表示顶点数。

表3 时间复杂度

从表3可知,DPA算法的时间复杂度为O(KE),最低,而BCLA算法的复杂度达到O(V2E2N)。MSBA算法的时间复杂度为O(V5E5)。从这些数据可知,提出的BCLA算法的时间复杂度高于DBA算法,但是低于MSBA算法。

5 总结

栅栏覆盖已广泛应用于边界检测。通过建立栅栏可有效地检测边界入侵者。而如何利用节点构建栅栏是实现栅栏覆盖的关键。本文提出基于学习机的栅栏构建算法。该算法充分学习机对环境学习能力,利用环境的反馈信号对动作集进行增强或减弱,进而选择最合适的节点构建栅栏。实验数据表明,提出的BCLA算法能够有效地构建栅栏,增加可建栅栏数。

后期,将研究节点能耗问题。即在满足栅栏覆盖要求的条件下,如何降低网络能耗,使得每条栅栏覆盖寿命能得到最大化,这将是后期研究工作的重点。此外,BLCH算法目的在于:利用有限的节点数,构建更多的栅栏数,用于检测入侵者。在实际应用中,可采用轮换机制,即多条栅栏轮流工作,进而降低网络能耗。这也是后期的工作重点。