基于CEEMD阈值和相关系数原理的MEMS陀螺信号去噪方法*

张 宁

(闽江学院物理学与电子信息工程学院,福州 350108)

MEMS陀螺在低成本惯性导航系统中已经得到了较为普及的应用。但MEMS陀螺的随机漂移误差具有典型的非平稳性、弱非线性特征,这将直接影响陀螺的精度。为此,需要对MEMS陀螺的随机漂移误差进行去除噪声处理,以提高陀螺使用精度。目前,对MEMS陀螺随机漂移信号进行去噪,其常用的处理方法是Kalman滤波法和小波分析方法。但Kalman滤波法会存在由于误差模型建立不准确而导致出现滤波发散的现象[1];小波分析法在MEMS陀螺信号去噪中已经取得了较多的成功应用[2-4],但小波分析方法并不是一种自适应滤波去噪方法,需提前设置小波基和分解级数,而这些设置对去噪的效果影响较大。

近年来,经验模态分解EMD(Empirical Mode Decomposition)[5]方法在滤波去噪领域被研究的较为广泛[6-7],这是一种可以对非线性、非平稳信号进行自适应分解的信号处理方法。但该方法存在有较为严重的模态混叠问题。为此,Wu等人提出通过对原始信号加入不同高斯白噪声,提出了一种集成经验模态分解EEMD(Ensemble Empirical Mode Decomposition)方法,可以有效减弱EMD方法中存在的模态混叠现象[8]。但是EEMD方法分解后的信号包含有残余噪声[9],在重构原始信号时将产生有较大的误差,并不具有完备性。在EEMD的理论基础上,Torres等提出了完备集成经验模态分解CEEMD(Complete Ensemble Empirical Mode Decomposition)方法[10],该方法通过对每一阶分解后的分量添加自适应的白噪声信号,并计算唯一的残差信号以获取固有模态函数IMF(Instrinsic Mode Function)。CEEMD方法不仅可以大大减轻模态混叠现象,而且可以精确重构原始信号[11]。

本文将CEEMD阈值滤波方法应用于MEMS陀螺信号去噪中来。通过CEEMD可以对原有随机漂移信号进行完备有效的分解,并利用相关系数原理准确判定噪声分量与有用分量的界限。在此基础上,考虑到高频噪声分量可能也包含有效成分,为此借鉴小波分析中的软阈值处理方式和EMD方法中的阈值计算模型,对含噪声高频分量采用阈值滤波去噪,并进而将其与有用分量相结合进行信号重构,以获得去噪后的随机漂移信号。通过对仿真信号和实际漂移信号进行分析,其结果表明本文所提出的方法可以有效抑制陀螺信号噪声,并取得良好的去噪效果。

1 理论背景分析

1.1 EEMD的基本原理

EEMD方法本质上是一种附加高斯白噪声的多次EMD分解的平均结果。其算法流程为:

①对原始信号x(t)多次添加均值为0,幅值标准差为一常数的白噪声ni(t),i=1…N,有:

xi(t)=x(t)+ni(t)

(1)

②对附加噪声信号xi(t)进行EMD分解,得到j个IMF分量和一个残余分量,记为IMFij(t)与ri(t)。

③对经历N次分解的每一个IMF进行总体平均计算,以得到最终分解结果,即为:

(2)

1.2 CEEMD的基本原理

①对原始信号x(t)添加不同的高斯白噪声ωi(t),则原始信号变为x(t)+ε0ωi(t),其中ε0为噪声系数。使用EMD方法进行I次分解,对其进行总体平均可得到第1个IMF分量为:

(3)

则第1个残余分量为:

r1(t)=x(t)-IMF1(t)

(4)

②定义算子Ej(·)为信号通过EMD分解后得到的第j个模态函数。对信号r1(t)+ε1E1(ωi(t))继续进行I次分解,可得到第2个IMF分量为:

(5)

③对于k=2,…,K,计算k阶残余分量为:

rk(t)=rk-1(t)-IMFk(t)

(6)

④提取信号rk(t)+εkEk[ωi(t)]的第1个IMF分量,定义k+1个模态函数分量为:

(7)

⑤重复执行步骤③和步骤④,直到残余信号不可再继续被分解为止,最终可得到K个模态函数分量,其最终残差分量为:

(8)

由上式原始信号x(t)可以被表示为:

(9)

从上述CEEMD方法的原理可以看出,CEEMD充分利用了EEMD噪声辅助分析的特点,并可对原始信号进行精确完整的重构。

2 CEEMD阈值滤波去噪模型

2.1 利用相关系数原理确定噪声层数

采用CEEMD方法对陀螺随机漂移信号进行有效分解后,为了对原信号进行去噪处理,关键在于要准确确定分解后的噪声分量和有用分量之间的界限。目前判定噪声层数常用的方法有排列熵[12]、Shannon熵[13]等,而在本文中将采用分解后的各个IMF分量与原始信号之间的相关系数来进行确定。相关系数的计算公式为[14]:

(10)

式中:L为信号长度,ρ(i)代表第i个IMF分量与原始信号x(t)之间的相关系数。

在计算出各个IMF分量的相关系数后,可以绘制出相关系数曲线图。经过作者对大量加噪仿真信号分解后分量进行计算的统计分析,得到相关系数与噪声层数之间存在一定的变化规律为:

①当含噪信号x(t)信噪比非常大时,第一阶IMF 处相关系数较小,从第二阶IMF起相关系数会突然增大,此时可以认为第一阶IMF为噪声分量;

②当含噪信号x(t)信噪比不是非常大时,从第一阶IMF到第(m-1)阶IMF的相关系数数值会呈现单调递减的趋势,直至第m阶时相关系数会逐渐明显增大。可以认为,第(m-1)阶前的所有IMF分量都为噪声分量。

通过相关系数曲线的变化规律,可以准确判定噪声层数。与排列熵、Shannon熵相比,相关系数原理判定噪声层数不仅准确,而且具有简易性的特点。

2.2 CEEMD阈值去噪流程

在确定噪声层数后,一般的去噪方法是直接将所有噪声分量置零,将有用分量重构即可获得去噪后的信号。在本文中,考虑到CEEMD方法由于借助了噪声辅助分析手段,分解后的高频噪声信号中可能还包含有效成分,为此借鉴小波软阈值的处理方式和EMD阈值的设置方法,对高频噪声分量进行阈值滤波处理,对其滤波后的分量与有用分量进行重构以达到信号去噪的目的。其具体去噪流程如下:

①对原始信号x(t)使用CEEMD进行分解,分解后得到K个固有模态函数分量IMF和一个残差分量R(t);

②使用式(10)计算各个IMF分量与x(t)的相关系数,以确定噪声层数为(m-1);

③对前(m-1)个IMF噪声分量使用阈值滤波。阈值处理形式采用软阈值方式:

(11)

(12)

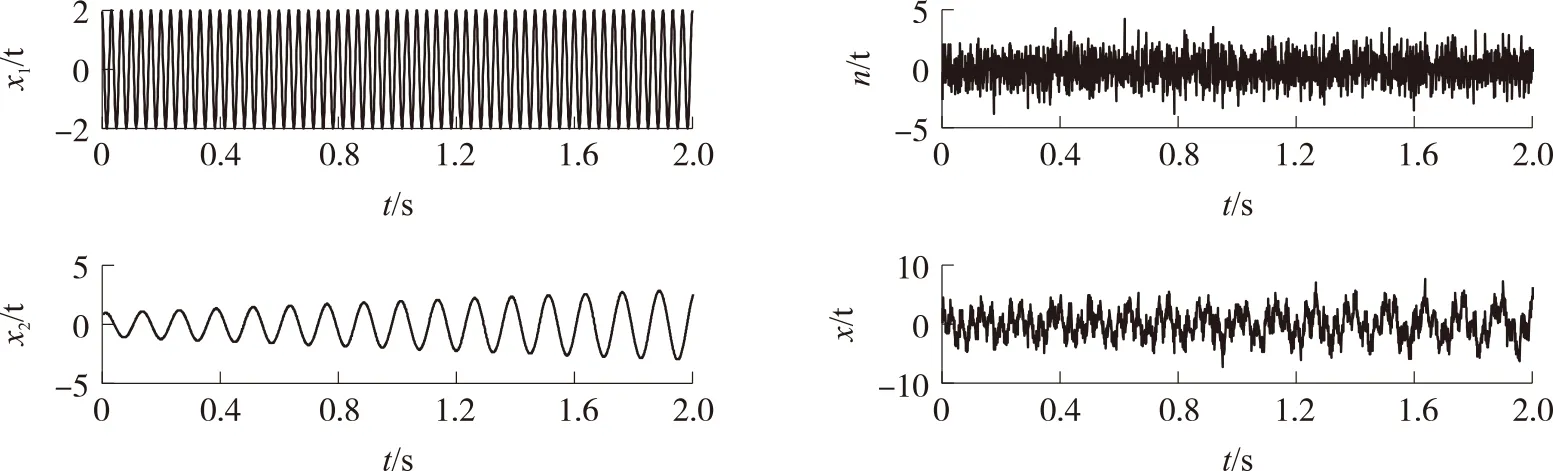
图1 仿真信号及其各组成成分

式中:C为一常数,Ei为第i阶IMF对应的能量,其值可以使用下列公式进行估计[17]:

(13)

此处E1为第一阶IMF对应的信号能量,采用如下公式进行计算:

(14)

④将阈值滤波后的噪声分量与有用分量重构,获得去噪后的信号:

(15)

2.3 去噪效果评价指标

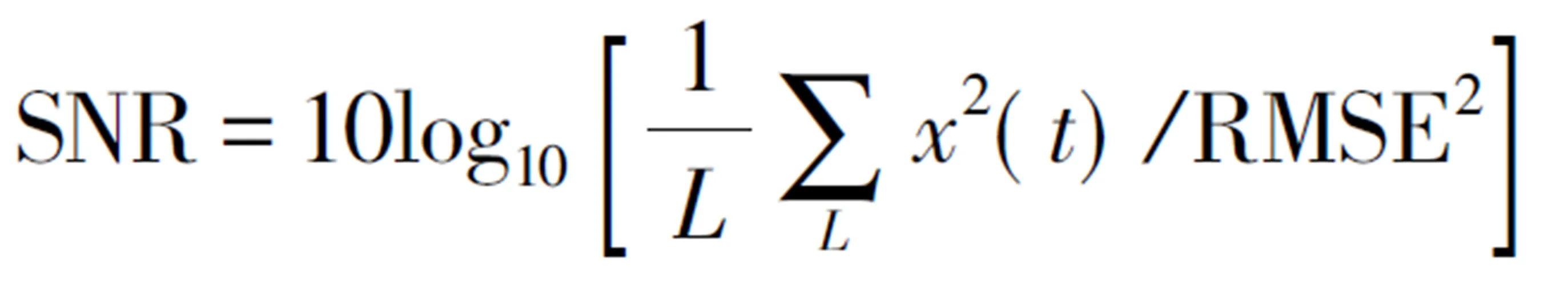
3 仿真算例分析

考察以下仿真信号:

x(t)=x1(t)+x2(t)+n(t)

(16)

式中:x1(t)=2sin(2π30t+π/2),x2(t)=(t+1)×sin(2π8t+π/3),t=1/1 000∶1/1 000∶2。n(t)是以x1(t)+x2(t)基础加入的信噪比为5 dB的噪声信号。仿真信号组成如图1所示。

对仿真信号分别采用EMD、EEMD、CEEMD 3种方法进行分解,其中EEMD、CEEMD方法中的噪声标准差都设为0.2,总体平均次数设为100。考虑到图形的显示效果,对于每种方法的分解结果只在图中列出了前8阶IMF,如图2～图4所示。

图2 EMD方法分解结果(前8个IMF)

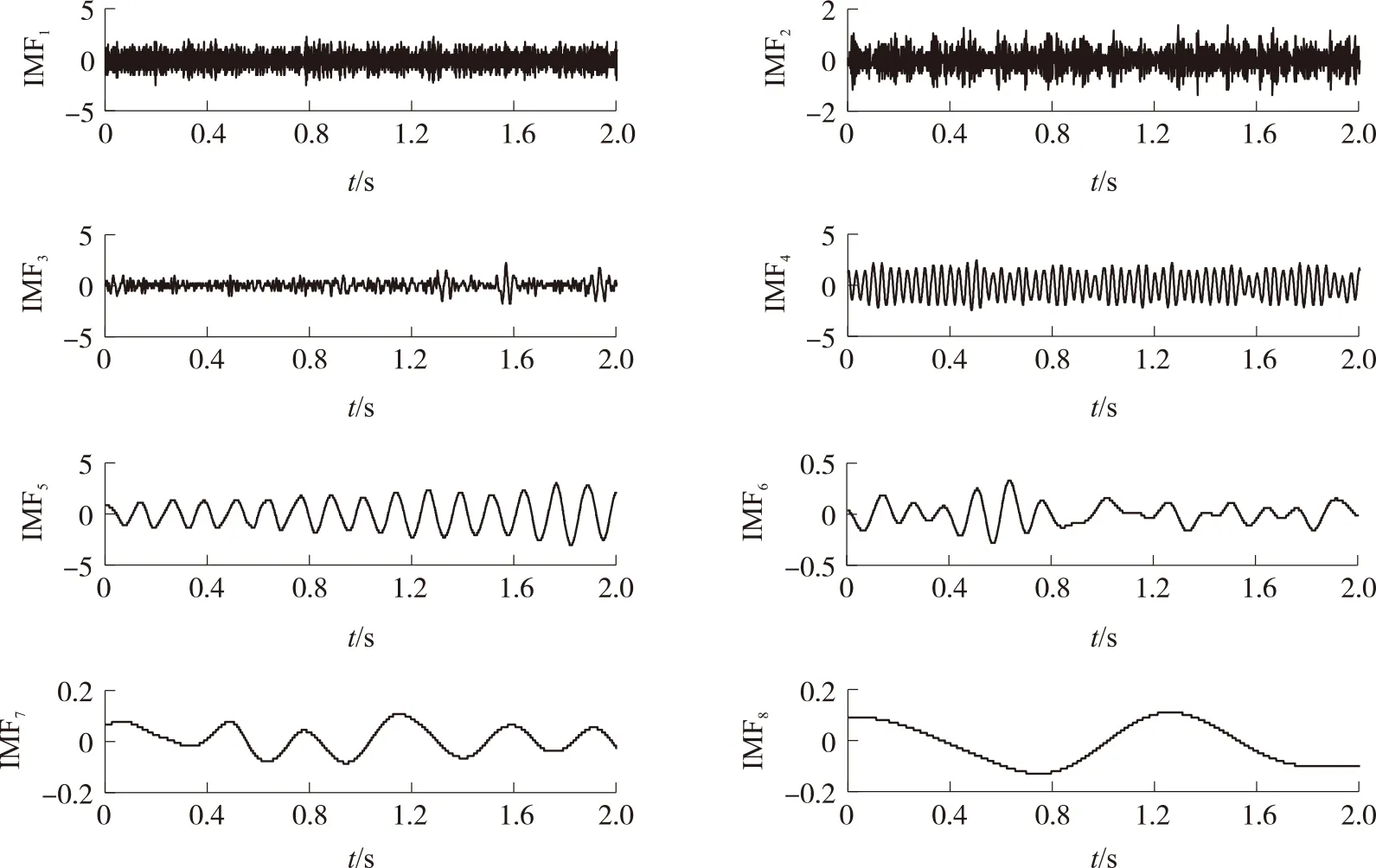
图3 EEMD方法分解结果(前8个IMF)

图4 CEEMD方法分解结果(前8个IMF)

从图2可以看出,EMD方法分解的第3、4阶IMF分量中产生了非常明显的模态混叠现象;从图3、图4可以看出,EEMD和CEEMD两种方法的分解结果较为有效的克服了模态混叠现象,并可有效的提取出原信号分量:在图3中,第4、5阶IMF分量分别对应仿真信号中的x1(t)、x2(t)分量;在图4中,第5、7阶IMF分量分别对应仿真信号中的x1(t)、x2(t)分量。为了进一步说明CEEMD方法的优越性,对3种方法分解后的分量加以重构,并与原始仿真信号对比以计算重构误差,结果如图5所示。信号的重构精度以均方根误差来评定,如表1所示。

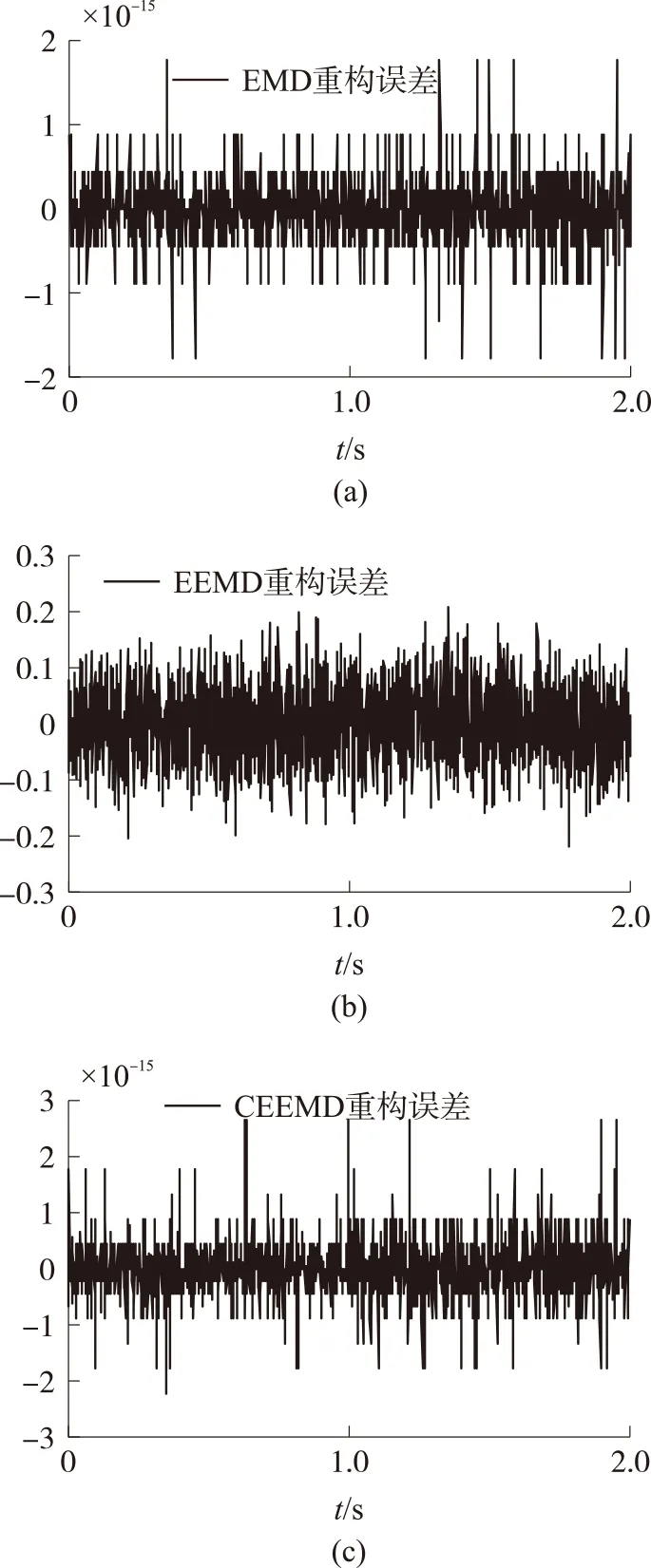
图5 3种方法的重构误差

信号分解方法EMDEEMDCEEMDRMSE3.580 4×10-160.047 43.941 0×10-16

从图5和表1可以看出,EMD方法和CEEMD方法的重构误差数量级为10-15,其重构精度达到10-16,因此可以忽略不计;而EEMD方法在噪声辅助分析下,虽然能够消除模态混叠的影响,但其重构误差较大。显然对于这3种自适应信号分解方法,CEEMD方法不仅可以消除模态混叠现象,而且能完备重构信号,因此在信号分解中具有明显的优越性。

为了使用CEEMD方法对仿真信号进行去噪,计算其分解后各个IMF与x(t)的相关系数,如图6所示。

图6 各个IMF与原始信号的相关系数

从图6中可以看出,从第1到4阶IMF有单调递减的趋势,至第5阶IMF相关系数明显变大,可以确定前4阶IMF为噪声分量。为了与本文所提出的CEEMD阈值去噪的效果进行对比,本文还对仿真信号分别使用了小波分析、EMD、EEMD、CEEMD方法进行去噪处理。其中EMD、EEMD、CEEMD使用的是强制去噪处理,即在判断出噪声层数后,直接舍去噪声分量进行重构以获得去噪后信号;小波分析法使用的是软阈值处理方式,设置的小波基函数和分解级数分别为sym3和7。去噪后的评价指标对比如表2所示。

表2 各种方法的去噪评价指标对比

从表2中可以看出,CEEMD阈值去噪方法在去噪后其信噪比最大,同时其均方根误差最小,表明该去噪方法最优;而小波分析方法效果最差;CEEMD强制去噪方法的去噪效果也要优于EMD、EEMD强制去噪方法。CEEMD阈值去噪方法的结果如图7所示,从中可以看出,大量随机噪声能够被有效去除。

图7 CEEMD阈值去噪结果

图8 MPU6050型陀螺仪

4 MEMS陀螺信号实例分析

实验中采用MPU6050型MEMS陀螺仪进行数据采集,该设备包括有三轴陀螺仪和三轴加速度计,如图8所示。

本文以X轴陀螺仪数据为例,以100 Hz的采样频率采集了一组静态数据,将其作为X轴陀螺仪随机漂移序列信号。截取该序列中的1 024个数据作为实验数据,如图9所示。

图9 陀螺漂移实验数据

对实验数据采用CEEMD方法进行分解,并计算各IMF分量与其实验漂移信号之间的相关系数,可以发现从第5阶开始显著增大现象,则确定前4阶IMF分量为噪声分量。进而使用阈值滤波,其去噪结果如图10所示。

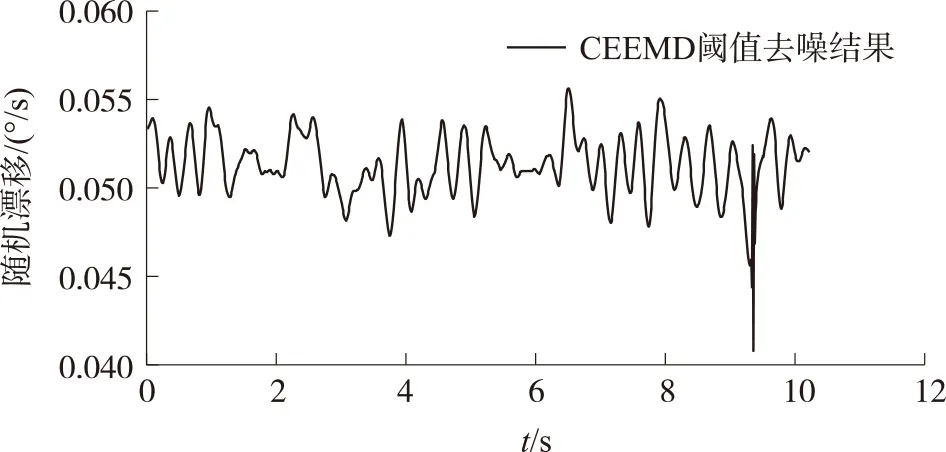
图10 陀螺漂移CEEMD阈值滤波结果

从图10可以看出,陀螺漂移信号噪声可以得到有效抑制。为了对比其去噪效果,与仿真信号算例类似,继续使用小波分析、EMD、EEMD、CEEMD 4种方法对其进行去噪。参数的设置与上述设置相同。去噪后的评价指标计算结果如表3所示。

从表3可以看出,CEEMD阈值去噪的效果仍然最优。几种方法的去噪效果可以得到与仿真算例一致的结论。

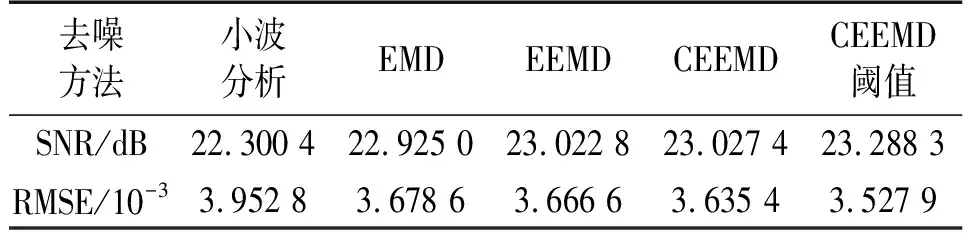
表3 各种方法对陀螺漂移信号的去噪评价指标对比

5 结论

本文充分分析了EMD、EEMD、CEEMD 3种自适应信号分解方法的优缺点。通过借鉴小波阈值处理方式和EMD阈值设置方法,在利用相关系数原理合理确定了分解后噪声分量与有效分量界限的基础上,提出了基于CEEMD阈值滤波的MEMS陀螺信号去噪方法。通过对仿真信号去噪结果分析可以得到如下结论:

①CEEMD阈值滤波方法的去噪效果要优于CEEMD、EEMD、EMD强制去噪方法和小波分析方法。仿真信号和实际数据算例结果充分表明了CEEMD阈值滤波去噪方法在MEMS陀螺漂移信号去噪中的应用具有可行性和有效性。

②尽管本文采用CEEMD阈值滤波方法相对于强制去噪方法提升了去噪性能,但在实际MEMS信号分析中,其提升的幅度并不大。考虑到本文采用的是软阈值函数,其在阈值处理过程中会造成一定程度的高频信息损失。为此,进一步的研究需要改进阈值函数,以更好的提升去噪性能。