基于椭球拟合的磁力计误差校正方法研究*

孙 伟,杨一涵,王 野

(辽宁工程技术大学测绘与地理科学学院,辽宁 阜新 123000)

MEMS磁力计工作时不存在累积误差,在当前状态没有干扰磁场的情况下可测量恒定不变的局部磁场矢量,利用该矢量完成载体航向角计算[1-4]。磁力计在实际环境中易受器件自身工艺和结构的限制和周围磁场的干扰导致测量精度降低,为获得更精确的磁场信息,就需要对磁力计进行校准[5]。椭圆拟合法局限于二维平面而无法对三维空间中的磁场信息进行校正[6];磁力计受到软、硬、铁磁场分别进行补偿校正方案存在速度慢效率低的弊端[7]。论文提出的基于椭球拟合校准算法,首先根据磁力计自身误差和软硬磁特性建立其误差模型,通过椭球拟合后利用利用最小二乘平差方法估计出椭球方程系数,从而得到校准后的磁场强度值,实验结果验证了算法可行性。

1 磁力计误差建模

1.1 器件固有误差建模

制作工艺和结构等引起的磁力计误差主要包括3个轴灵敏度不一致造成的刻度因子误差[8]、安装过程中出现的3个轴非正交误差和零偏误差[9]。

建立误差模型:

Hm=KPHb+Bd

(1)

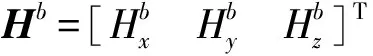
1.2 环境扰动建模

外部环境干扰主要包括硬铁干扰和软铁干扰[10]。硬铁干扰在载体上的永久磁铁或磁化介质等硬磁材料上产生,在没有外界磁场作用时不产生磁性,而当这种材料受到外界磁场作用会发生磁化,其自身产生一个不受外界磁场影响、不随时间位置变化的固定磁场,其磁场强度和方向保持不变,由于硬磁材料和传感器都固定在载体上,所以不会随载体姿态变化而变化。由硬铁干扰产生的磁场会导致磁力计输出产生偏差,因此硬铁模型是磁力计各轴输出值与一个偏置矢量R相加的和,为一固定常值;软铁干扰主要由地磁与软磁材料之间的相互作用引起,与硬磁材料不同的是,软磁材料被周围环境磁场磁化后产生的磁场的磁场强度与方向和外界磁场有关,会随着外界磁场的磁场强度大小和方向的变化而变化因此软铁模型是磁力计各轴输出值前乘以一个系数矩阵L。得到考虑环境因素建立的磁力计误差模型为:

(2)

结合式(1)和式(2),得到磁力计误差模型:

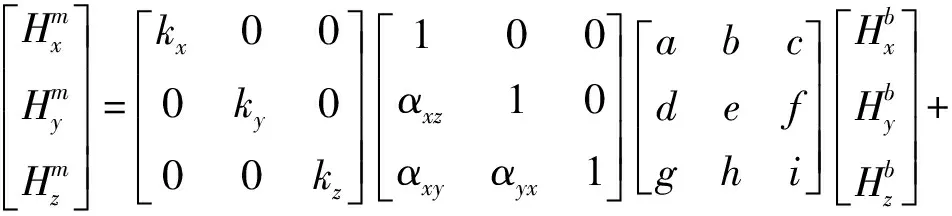
(3)

即:

Hm=DHb+B

(4)

式中:矩阵D为3个系数矩阵的乘积;矩阵B为零位偏差Bd和硬磁误差Bh的和。磁力计中存在的传感器噪声对输出值的影响可忽略不计,因此在模型中给予忽略。对式(4)进行转换,可将磁力计存在误差干扰的输出值校准为实际磁场中真实值:

Hb=D-1(Hm-B)=E(Hm-B)

(5)

式中:E为矩阵D的逆矩阵。

2 椭球拟合校准算法

2.1 椭球拟合原理

在环境不变的情况下,传感器每个姿态感受的磁场强度是相同的。在没有偏差和传感器内部x,y,z轴相互垂直的情况下,磁力计测量的x,y,z轴的值可在三维空间中组成一个球面。但是在实际工作环境中的磁力计受刻度因子、三轴非正交和零偏等误差及外界环境中硬、软铁等误差影响,使得3个敏感轴输出数据构成一个球心偏离坐标系原点的椭球[10-11]。因此磁通量在三维空间组成的椭球球心坐标是磁力计校准的一部分。

二次曲面方程的一般形式:

(6)

写成矩阵形式后简化:

(7)

2.2 椭球拟合算法

利用椭球拟合方法进行磁力计误差校正的实质就是通过椭球拟合算法算出球心坐标和椭球方程系数,将球心拟合到坐标系原点,并且通过求得的系数得到校准矩阵和偏移矢量,以得出磁场强度的真实值从而达到校正误差的目的。

由磁力计综合误差模型构成椭球方程:

(Hb)T(Hb)=[E(Hm-B)]T[E(Hm-B)]
=(Hm)TC(Hm)-2BTACHm+BTCB

(8)

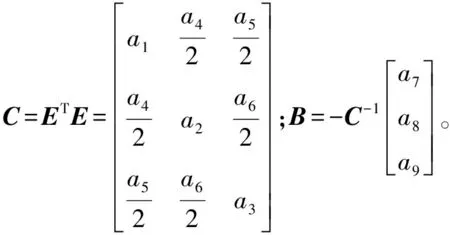
由磁力计测量值数据得出线性方程组:

(9)

最后要使残差e最小,以磁力计采集的原始数据与椭球面的距离平方和最小为判断准则,应用最小二乘估计法得出椭球方程各个系数,

(10)

因此,可求得校准矩阵E和偏移矢量B。

3 实验结果及分析

采用实验室现有的MTi-G-710型MEMS惯性测量单元内置磁传感器搭建测试环境,技术指标如表1所示[12-13]。

表1 Mti-G-710内置磁力计性能指标

为验证椭球拟合算法可行性,在传感器周围固定一个铁块模拟工作环境下的磁干扰,实验环境如图1所示。

图1 实验环境

将传感器在三维空间中任意旋转5 min,使采集的数据尽可能覆盖整个椭球面,基于本文提出的算法利用MATLAB软件处理原始数据,应用最小二乘法可求出拟合的椭球方程各系数为:

σ=[1.140 4,1.080 6,1.113 0,-0.014 6,-0.009 3,

0.018 6,-0.001 2,0.028 3,-0.262 8]

得到校准矩阵E和偏移矢量B:

将校准矩阵E和偏移矢量B代入式(8)即可得到校正后的磁力计输出。

根据图2所示对比修正前后磁场强度曲线,解算出表2所示的两球球心坐标。可看出原始数据在坐标系中形成的轨迹原点由于自身误差和周围磁场干扰导致其偏离坐标原点,经过椭球拟合误差校正之后的磁场强度数据拟合的球体球心更接近坐标系原点。

图2 校正前后磁场强度对比曲线

xyz校正前0.002 60.030 20.236 7校正后0.000 20.000 70.010 0

将磁力计输出的原始磁场强度模值与校正后的磁场强度模值进行对比(如图3)后发现:校正后的磁场强度模值波动小于原始磁场强度模值,校正后的磁场强度标准差为0.0519远小于校正前磁场强度标准差0.146 2。

图3 磁场强度模值比较曲线

4 结论

论文提出一种磁力计椭球拟合误差校正算法,基于误差模型建立椭球拟合校正模型,利用最小二乘法解算出校准矩阵和偏移矢量得到校准后磁场值。实验结果表明椭球拟合算法可有效降低器件自身误差及外界硬、软铁干扰等引起的器件输出误差,实现对三维磁力计的有效校正,可进一步提高载体运动信息获取的准确性和实时性。