主卷扬布置对旋挖钻机动臂变幅机构动力学特性的影响
许怡赦,康辉梅
(1.湖南机电职业技术学院电气工程学院,湖南 长沙410151;2.湖南师范大学工程与设计学院,湖南 长沙410081)
旋挖钻机是一种大直径深孔灌注桩成孔施工的高端装备,广泛应用于铁路、公路和桥梁等桩基施工领域[1-4]。如图1所示,旋挖钻机动臂变幅机构由回转平台、连杆、三角架和动臂组成,构成平行四边行,主要用于钻桅的水平起落和钻孔作业半径的调整。

图1 旋挖钻机整机示意图
旋挖钻机动臂变幅机构的动力学分析属于多刚体系统动力学分析,主要研究动臂变幅机构在不同工况下的动力学逆问题。康辉梅等[5,6]采用牛顿-欧拉方法分析了变幅工况下四种不同动臂变幅机构的动力学特性,以及提钻工况下动臂变幅油缸载荷特性以及回转平台的约束反力;基于动静法建立动臂变幅机构动力学模型的基础之上,何清华等[7]分析了变幅工况下动臂变幅油缸载荷和回转平台约束反力随钻桅倾角和动臂转角的变化规律;徐信芯等[8]分析了大三角变幅型旋挖钻机提钻和钻进工况下动臂变幅油缸和回转平台约束反力的载荷特性。利用多刚体动力学仿真软件ADAMS建立虚拟样机,朱建新[9]和腾召金[10]分析了变幅工况下动臂变幅油缸的举升特性,夏背[11]也分析了钻进和提钻工况下动臂变幅油缸的载荷特性,并探讨了回转平台的约束反力。
旋挖钻机工作部件参数也强烈影响动臂变幅机构的动力学性能。何清华等[7]分析了动臂变幅时钻桅上不同位置的动力头和钻杆对动臂变幅油缸载荷的影响;许怡赦等[12]探讨了动臂变幅机构安装角度对动臂变幅油缸载荷和回转平台约束反力的影响。
实际上,作为提升和下放钻具的主卷扬也是旋挖钻机的一个重要工作部件,其位置也会影响动臂变幅机构动力学性能,但是,较少有文献报道这方面的研究[13,14]。因此,在前期旋挖钻机动臂变幅机构动力学特性研究的基础上,本文主要研究变幅工况和提钻工况下主卷扬布置对动臂变幅机构动力学性能的影响。
1 数学模型
1.1 主卷扬位于回转平台
1.1.1 变幅工况
变幅工况下、主卷扬位于回转平台上,旋挖钻机工作装置的受力图如图2所示。FN表示动臂变幅油缸载荷,Tj为主卷扬钢丝绳拉力,G2、G3、G4、G5、G6和G7分别表示连杆、三角架、动臂、动力头、钻杆和钻桅的重力。为便于研究,进行如下必要的假设:
1)钻桅变幅油缸自锁,钻桅倾角ξ为任意值;
2)连杆和动臂与水平面的夹角、角速度和角加速度分别为β、ω和ε;钻桅变幅机构及其上的动力头皆作平动,每一瞬时各质点的加速度相同。
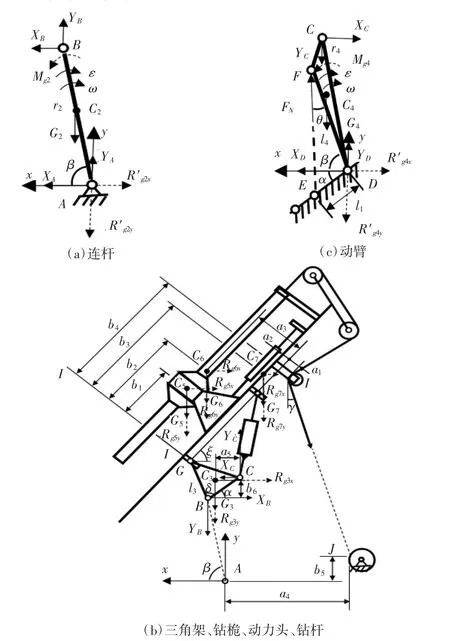
图2 变幅工况下、主卷扬位于回转平台上工作装置受力
据图2(a)所示,连杆绕A点定轴转动,惯性力系简化为通过 A 点的力 R′g2x、R′g2y和力偶 Mg2,大小分别为:

Mg2=I2Aε
式中,I2A为连杆绕A点的转动惯量。ac2x和ac2y分别为连杆质心加速度的x和y分量,其大小可由连杆质心坐标二次求导得出:
ac2x=-εrc2sinβ - ω2rc2cosβ
ac2y= εrc2cosβ - ω2rc2sinβ
rc2为连杆质心C2至回转中心A的距离。
据图2(b)所示,动臂绕D点定轴转动,惯性力系简化为通过 D 点的力 R′g4x、R′g4y和力偶 Mg4,大小为:

Mg4=I4Dε
式中,I4D为动臂绕通过D点定轴的转动惯量。ac4x和ac4y为动臂质心加速度的分量,其大小可由动臂质心坐标的二次求导得出:
ac4x=-εrc4sinβ - ω2rc4cosβ
ac4y= εrc4cosβ - ω2rc4sinβ
rc4为动臂质心C4至回转中心D的距离。
据图2(c)所示,三角架、钻桅、动力头和钻杆作平动,惯性力系简化为通过各刚体质心的力Rgix和Rgiy(i为3、5、6和7),大小为:
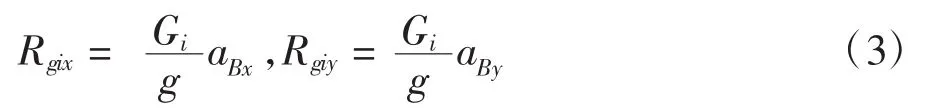
式中,aBx和aBy为三角架、钻桅、动力头和钻杆的质心的加速度,大小为:
aBx=-εr2sinβ - ω2r2cosβ
aBy=-εr2cosβ - ω2r2sinβ
r2为连杆长度即铰点A、B间的距离。
根据达朗伯原理,质点系的主动力、约束反力和惯性力组成平衡力系,图2所示的三组平衡方程用式(4)-(6)表示为:


式(5)中:r4为铰点 D、C 间的距离,l4为铰点 D、C 间 的距 离 ,σ = ∠CDC4,η = ∠CDF,θ= arcsin为铰点 D、E 间
的距离。式(6)中:Tjx=Tjsinγ,Tjy=Tjsinγ,Tj=G6sinξ,γ为钢丝绳与铅锤方向的夹角,其大小为:γ为三角架质心与铰点C间的垂直距离,为铰点B、C间的距离,a5为三角架质心与铰点C间的水平距离,b3为铰点G、钻桅质心沿平行钻桅方向的距离,a2为钻桅质心与钻桅的垂直距离,l3为铰点B、G间的距离,b1为铰点G、动力头质心沿平行钻桅方向的距离,a3为动力头质心与钻桅的垂直距离,b2为铰点G、钻杆质心沿平行钻桅方向的距离,b4为铰点G、I沿平行钻桅方向的距离,a1为铰点I与钻桅的垂直距离,α为铰点C、B的连线与水平面的夹角,δ=∠CBG.当C5、C6位于 I-I线以上时,b1、b2取正号,当 C5、C6位于 I-I线以下时,b1、b2取负号。
1.1.2 提钻工况
提钻工况下、主卷扬位于回转平台上,旋挖钻机工作装置的受力情况如图3所示。主卷扬所受拉力由钻杆与钻渣等的重力G6、提升阻力R、启动阶段钻渣和钻杆等所受的惯性力R′g和泥浆产生的浮力F构成,即 Tj=G6+R+R′g-F,R′g= (G6/g)·(△v/△t),△v为提升速度变化量,可取为最大卷扬速度,△t为启动时间。钻桅还受到动力头重力G5引起的偏矩 M2,M=G5·(a3-a6).

(续下图)
(接上图)

图3 钻进工况下、主卷扬位于回转平台上工作装置的受力
以钻桅为研究对象,列出其平衡方程为:

以连杆为研究对象,列出其平衡方程:以动臂为研究对象,列出其平衡方程:


以C点为研究对象,列出其平衡方程:
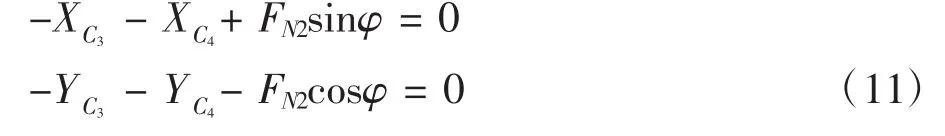
则动臂变幅机构各铰点约束反力和油缸载荷可由各刚体的平衡力系即式(7)-式(11)获得。
1.2 主卷扬位于钻桅下部
主卷扬位于钻桅下部,主卷扬滚筒对主卷扬钢丝绳拉力视为内力即图2和3中Tj=0,在平衡力系方程组中不考虑该拉力的力矩。因此,当主卷扬安装在钻桅下部、变幅工况下式(4)和(5)不变,只需将Tjx=0和Tjy=0代入式(6),可得三角架、动力头、钻桅和钻杆所组成的平衡力系:

当主卷扬安装在钻桅下部、提钻工况下式(8)至式(11)不变,只需将 Tj=0、Tjx=0和 Tjy=0代入式(7)可得钻桅的平衡力系为:

2 算例分析
以SWDM-2型旋挖钻机为例,在Matlab中进行算例分析。钻桅倾角ξ的取值范围为[0,95°],动臂转角β的变化范围为[0,76°]。变幅工况下钻桅启动和停止时角加速度ε为0.087 rad/s2;忽略提钻工况下钻渣重力,提升阻力和泥浆浮力等。
2.1 变幅工况
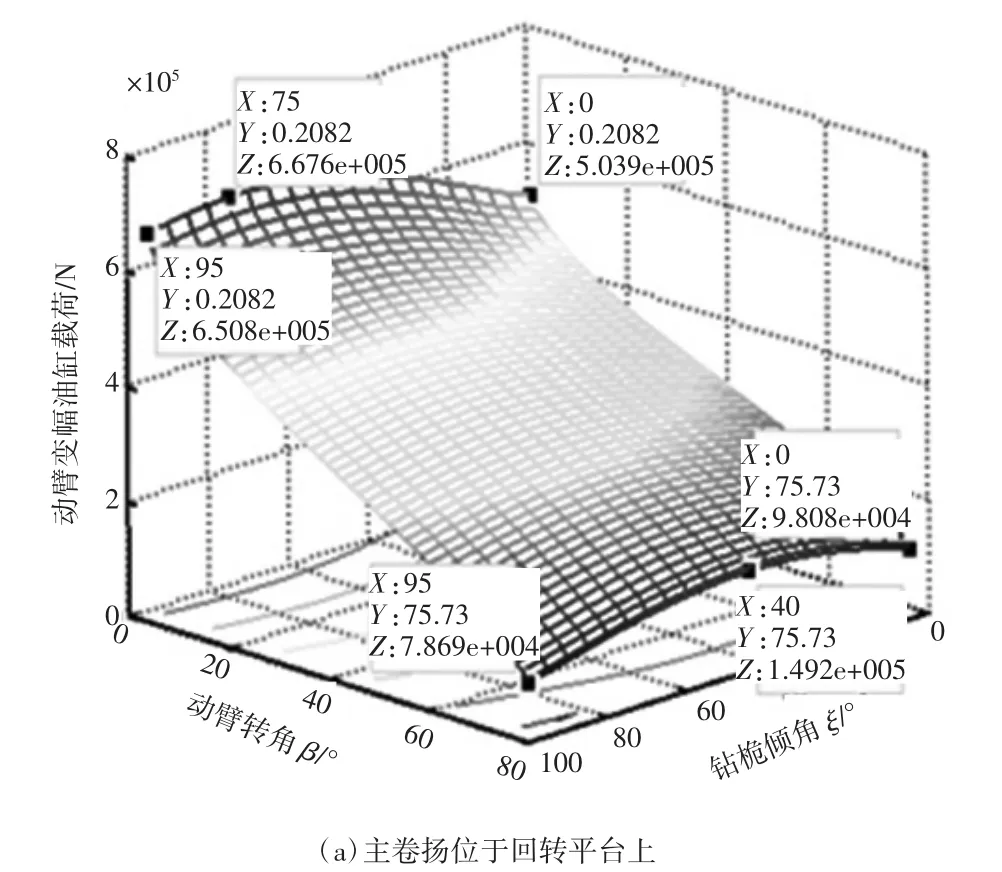
图4所示为变幅工况下两种主卷扬的布置对旋挖钻机动臂变幅油缸载荷特性的影响,在钻桅倾角为0时,不论主卷扬位于回转平台还是钻桅下部,动臂变幅油缸的启动载荷相同,并且在动臂变幅启动之后,动臂变幅油缸载荷随动臂转角的增大而减小。
(续下图)
(接上图)

图4 变幅工况下动臂变幅油缸载荷特性
由图4(a)可知,主卷扬位于回转平台上钻桅倾角会影响动臂变幅油缸载荷的力学性能,当钻桅倾角为75°时动臂变幅油缸的启动载荷最大;当钻桅倾角为0°时动臂变幅油缸的启动载荷最小,因此实际变幅操作过程中应优先进行动臂变幅。在任意动臂转角处,随钻桅倾角的增大动臂变幅油缸载荷先增大而后减小,并且动臂转角较大时动臂变幅油缸载荷极大值所对应的钻桅倾角较小。也就是说,当钻桅倾角较大时动臂变幅油缸载荷的下降程度较小和变化趋势较缓和。因此,在实际变幅操作过程中,动臂变幅启动之后应交替进行钻桅变幅和动臂变幅,并在某个适当的动臂转角处进行钻桅变幅完成立钻操作。
由图4(b)可知,主卷扬位于钻桅下部钻桅倾角不会影响动臂变幅油缸的力学性能,也不会影响旋挖钻机的变幅工艺。对比图4(a)和(b)可知,主卷扬位于钻桅下部动臂变幅油缸载荷可以认为是主卷扬位于回转平台上动臂变幅油缸载荷的一个特例,这是因为当钻桅倾角为0°时钢丝绳拉力对动臂变幅油缸载荷没有影响。因此,在随后的实验研究中只考虑主卷扬位于回转平台上旋挖钻机动臂变幅油缸的动力学性能。
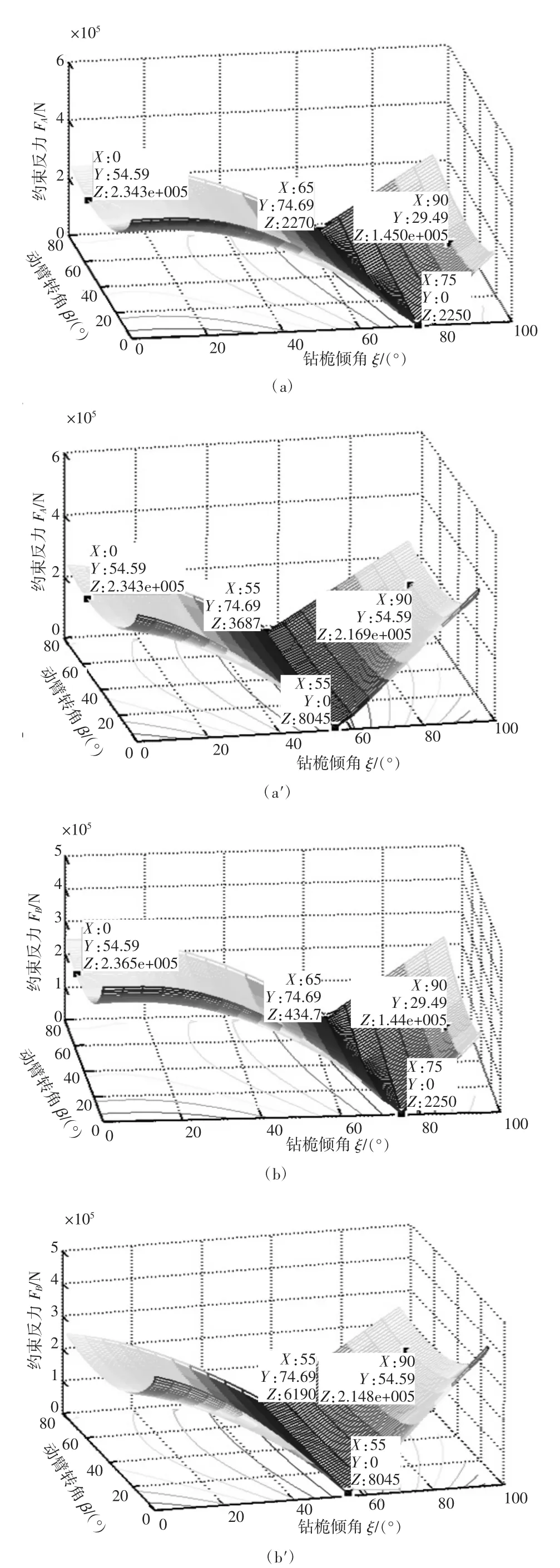
不同钻桅姿态下动臂变幅过程中动臂变幅机构各铰点受力特性如图5所示。由图5可知,不论主卷扬位于回转平台上还是钻桅下部,铰点A、B、C和D的受力具有相同的变化趋势。对于任意动臂转角铰点A、B和C的受力随钻桅倾角的增大先减小后增大;对于任意钻桅倾角铰点A、B和C的受力随动臂转角的增大也先减小后增大,不过,其变化幅度较小。由于铰点A和B位于连杆的两端,它们的受力基本一致。因为铰点A、B和C受力随钻桅倾角的增大明显减小,所以在实际变幅过程中,动臂变幅启动后应该进行钻桅变幅。
(续下图)
(接上图)
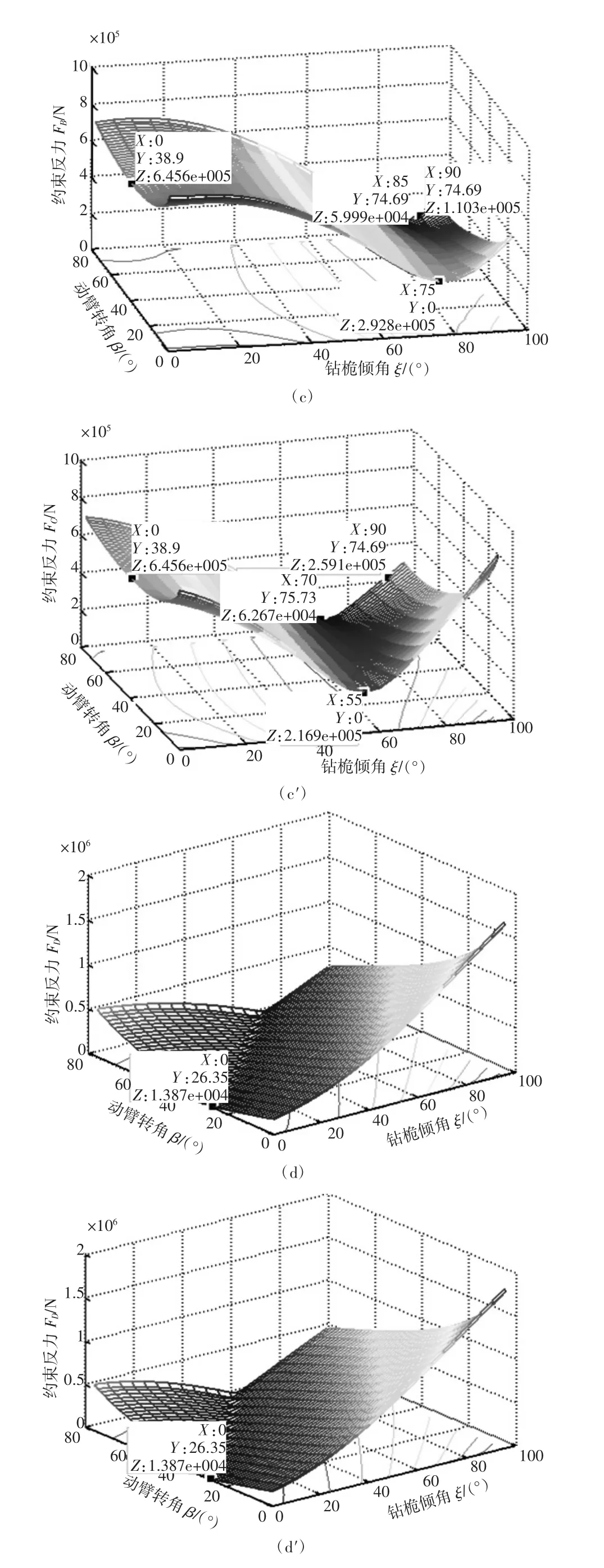
图5 变幅工况下动臂变幅机构各铰点的动力学特性
与其它三个铰点相比,铰点D受力更大以及变化幅度更显著,因此在旋挖钻工作装置中可以只要考虑铰点D的动力学特性。
(a)、(b)、(c)和(d)分别为主卷扬位于回转平台上铰点A、B、C和D点的约束反力
由图5(d)可知,在钻桅倾角为0°时进行动臂变幅,铰点D的受力较小,且在动臂转角为30°左右时,铰点D的受力达到最小值。在动臂转角为0°时进行钻桅变幅,铰点D的受力会急剧增大。由此说明,在旋挖钻机立钻过程中动臂变幅优先进行,在动臂转角达到30°左右时停止动臂变幅、进行钻桅变幅。根据图5(d)还可知,在动臂转角达到30°左右时如果只进行钻桅变幅,铰点D的受力也会急剧增大。因此,在实际变幅操作过程中为保持铰点D受力始终较小,动臂变幅和钻桅变幅应交替进行。
与主卷扬位于回转平台上相比较,主卷扬位于钻桅下部动臂变幅机构各铰点表现出如下不同的特性:①各铰点受力更大以及变化幅度更显著;②对于不同的动臂转角,铰点C受力的最小值出现在不同的钻桅倾角处;③对于不同的动臂转角,铰点B和A受力的最小值所对应的钻桅倾角不变。
因为当主卷扬位于回转平台上各铰点受力较小以及变化幅度较平缓,所以对于动臂变幅机构各铰点受力而言主卷扬安装在回转平台上优于安装在钻桅下部。并且,在随后的仿真分析中只考虑主卷扬位于回转平台上旋挖钻机动臂变幅机构铰点D的动力学性能。
2.2 提钻工况
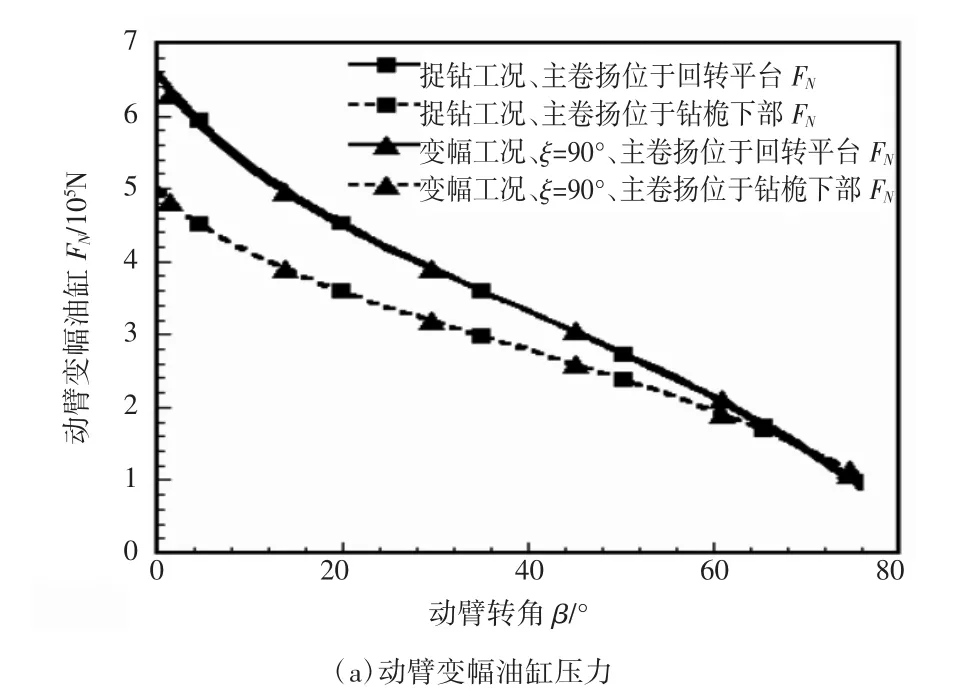
图6所示为提钻工况下(钻桅倾角为90°)动臂变幅机构的动力学特性,与主卷扬位于回转平台上相比较,主卷扬位于钻桅下部动臂变幅油缸载荷较小,而动臂变幅铰点约束反力较大;不论主卷扬位于回转平台还是钻桅下部,提钻工况下动臂变幅油缸载荷和铰点D约束反力均随动臂转角的增大而减小。
(续下图)
(接上图)
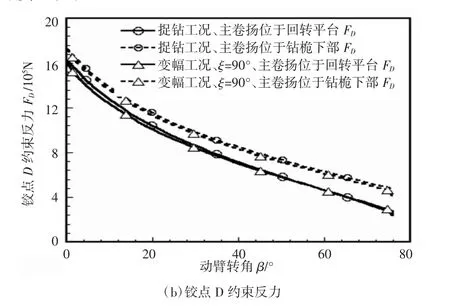
图6 提钻工况下动臂变幅机构的动力学特性
此外,对比图5中变幅工况、钻桅倾角为90°和提钻工况下动臂变幅机构动力学性能可知:在不考虑钻渣重力,钻土阻力和泥浆浮力等外部因素的影响,提钻工况下动臂变幅机构动力学特性只是变幅工况下动臂变幅机构动力学特性的一个特例。在实际提钻工况下、考虑这些外部因素时只是主卷扬拉力增加,图5中重合曲线离散为平行曲线,且提钻工况下动臂变幅油缸载荷和铰点约束反力增大。因此,在随后的仿真和实验研究中只考虑变幅工况下动臂变幅机构的动力学性能。
3 ADAMS仿真分析
在Solidworks中建立旋挖钻机工作装置的三维实体模型,并将其导入ADAMS中;在ADAMS中添加各零件之间的约束关系,形成的仿真模型如图7所示。

图7 旋挖钻机工作装置仿真模型
图8所示为主卷扬位于回转平台上动臂变幅机构动力学性能仿真曲线。钻桅倾角为0°时和90°时动臂变幅油缸载荷仿真值不相同,铰点D约束反力仿真值也不相同,他们随动臂转角的变化关系与图4(a)和图5(d)的理论描述相同。图9中实线的重合性说明当主卷扬位于钻桅下部钻桅倾角并不影响动臂变幅油缸载荷,动臂变幅油缸载荷和铰点D约束反力随动臂转角的变化关系也与图4(b)和图5(d′)的理论描述相同。尽管仿真模型误差使得仿真值和理论值之间存在差异,但是他们随动臂转角变化的一致性说明数学模型的正确性。
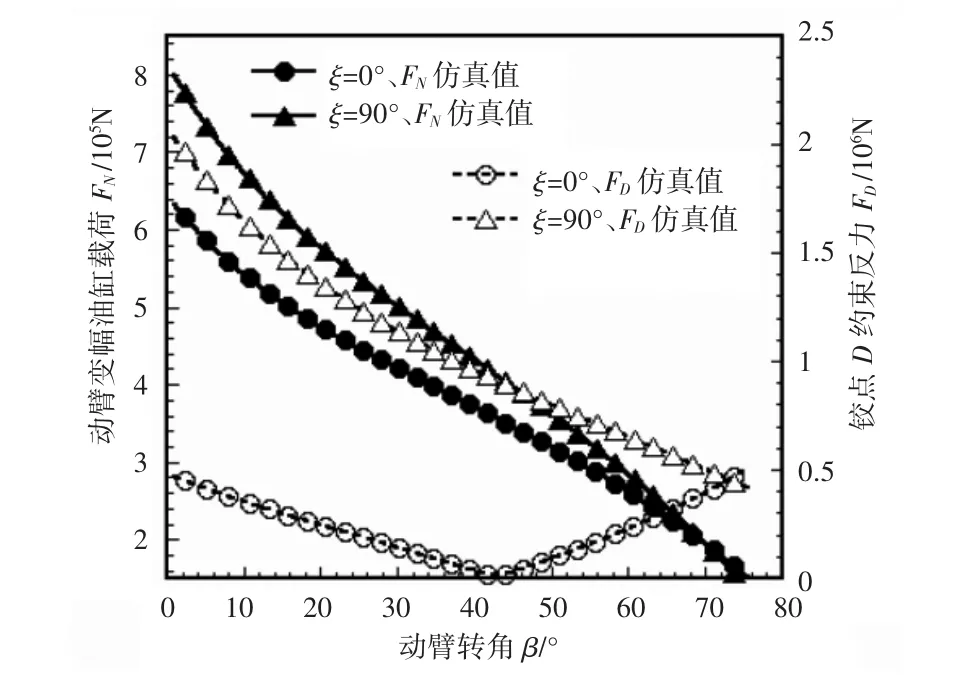
图8 主卷扬位于回转平台动臂变幅机构动力学性能仿真曲线

图9 主卷扬位于钻桅下部动臂变幅机构动力学性能仿真曲线
4 实验
实验用旋挖钻机为SWDM-2型全液压多功能旋挖钻机。动臂变幅油缸有杆腔和无杆腔压力通过压力传感器获得,传感器安装在动臂变幅油缸平衡阀的入口处如图10所示,动臂变幅油缸载荷由所测油缸压力和油缸结构参数计算所得。根据图4(a)和图8的分析,本实验仅测试主卷扬位于回转平台以及钻桅倾角为0°或90°时动臂变幅油缸压力随动臂转角的变化关系如图11所示。

图10 动臂变幅油缸压力测试图
对比图11的理论值、仿真值和实验数据可知,三者随动臂转角的变化趋势基本一致,由此说明了数学模型和仿真模型的正确性;当动臂角度较低时进行钻桅变幅,动臂变幅油缸载荷的稳定性较好;此外,该实验结果也说明实际变幅过程中动臂变幅和钻桅变幅应该交替进行。
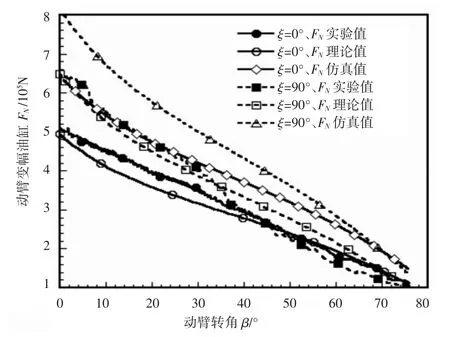
图11 主卷扬位于回转平台动臂变幅油缸载荷
5 结论
本文建立了不同工况下、不同主卷扬布置时动臂变幅机构动力学模型,同时分析了主卷扬布置对动臂变幅机构动力学性能的影响,并对该影响进行了ADAMS仿真和实验验证。研究结果如下:
(1)变幅工况下,不论主卷扬位于回转平台上还是钻桅下部,动臂变幅优先启动;在动臂变幅启动阶段动臂变幅油缸载荷和各铰点约束反力的启动特性与主卷扬的布置方式无关,动臂变幅油缸载荷为最大值;在动臂变幅启动之后,动臂变幅油缸载荷随动臂转角的增大而显著减小,各铰点约束反力随动臂转角的增大而先缓慢减小后缓慢增加。
(2)在钻桅变幅启动之后,主卷扬位于回转平台上动臂变幅油缸载荷随钻桅倾角的增大而先缓慢增加后缓慢减小,而主卷扬位于钻桅下部动臂变幅油缸载荷与钻桅倾角无关;不论主卷扬位于回转平台上还是钻桅下部,随钻桅倾角的增大,连杆与回转平台、连杆与三角架以及动臂与三角架的铰点约束反力均先减小后增大,动臂与回转平台的约束反力显著增大。
(3)对于动臂变幅油缸载荷的稳定性和立钻时铰点约束反力而言,主卷扬位于回转平台优于钻桅下部。在不考虑钻具重力和泥浆浮力等影响下,提钻工况下动臂变幅机构的动力学性能与变幅工况下钻桅倾角为90°时动臂变幅机构的动力学性能相一致。
此外,在旋挖钻机立钻过程中,当动臂转角达到30°左右时应交替进行钻桅变幅和动臂变幅,且在适当的动臂转角处进行钻桅变幅完成立钻操作。

