基于态势预测的非常规突发事件应急决策模型构建

杨继君，曾子轩

（1.国家行政学院应急管理培训中心，北京100089；2.广西财经学院 管理科学与工程学院，南宁530003）

0 引言

近些年来，一系列非常规突发事件比如“5.12”汶川大地震、“6.1”东方之星沉船事件以及“8.12”天津港大爆炸事故等不断冲击公众视线，考验着政府的应急处置能力和应急决策水平。这类突发事件的共同特点是[1]：其爆发具有突发性和不可预测性；危机的发展具有高度的动态性和不确定性；所造成的结果具有深度危害性。如何依据非常规突发事件的演化态势快速制定有效的应对方案是应急决策者面临的首要现实问题。首先对非常规突发事件发展态势进行分析和预测，在此基础上制定应对方案是科学决策的前提，在实践中发挥着越来越重要的作用。

态势预测是指在一定的时间和空间范围内，识别、理解环境因素，并且对事物的未来发展趋势进行预测。目前，态势预测在网络安全中进行了大量的研究，取得了较为丰富的研究成果[2-4]，但在突发事件特别是非常规突发事件中的研究比较少见，仅有少数学者对突发事件的某一特定类型或某一方面进行了研究。比如，Turoff等[5]提出将基于信息的态势预测引入到突发事件应急管理中，认为应该将对各类应急信息的获取和判断纳入到组织的例行管理中。杨继君等[6]从应急资源需求的角度建立了非常规突发事件态势演化模型，为应急决策者在突发事件爆发后应急救援物资的调度提供决策支持。宗芳等[7]通过建立Ordered Probit模型对交通事故中受伤人数进行预测，可为交通管理部门迅速准确预测事故态势。任福民等[8]对国内外在极端气象事件的态势监测和预测方法进行了总结，并对极端气象事件的监测和预测业务发展及相关科学问题给出了展望。刘怡君等[9]从信息、网民、心理和观点四个纬度构建了非常规突发事件社会舆论超网络模型，可对非常规突发事件的社会舆论演化态势进行预测，卞曰瑭等[10]也做过类似研究。本文在上述研究成果的基础上，从非常规突发事件演化的信息流出发，以序贯博弈理论为分析工具，构建基于态势预测的非常规突发事件应急决策模型，为探索非常规突发事件态势演化规律提供新方法，同时也为应急决策提供更为准确、科学的参考依据。

1 非常规突发事件应急决策的序贯博弈过程分析

局中人决策有先后顺序的动态博弈，统称为序贯博弈[11]。序贯博弈使用序贯理性假设[12]，即在给定的信念下，局中人的策略必须是序贯理性的。可以认为，局中人要根据他们对未来可能结果的权衡，决定当前的行动策略。从应急决策过程上讲，鉴于非常规突发事件的一系列特殊属性，应急决策者必须依据非常规突发事件（后简称“突发事件”）的阶段性处置结果和演化态势动态调整应急处置与救援方案，也就是说，应急决策者制定的应急处置与救援方案不是一次性完成的，而是随着对事态信息的不断收集与完善来动态调整应对方案，这种对应对方案的动态调整过程就类似于博弈论中的序贯博弈过程。

应急决策中的序贯博弈过程有如下几个主要特征[13]：（1）突发事件是动态发展变化的，它随着应对方案的实施而由一种状态向另一种状态转化；（2）突发事件的信息不断完善，从模糊到清晰，从不完全到完全；（3）在信息不完全条件下所制定的应对方案能够便于在信息完全时刻及时调整；（4）应急决策者是根据突发事件所处状态和阶段性的救灾成果对其信念进行修正而生成新的应对方案。下面以图1为例简要描述这一过程，在此规定，序贯博弈中的2个局中人为突发事件和应急决策者。

图1 应急决策的序贯博弈过程模型

（1）从t0→t1为T0阶段，突发事件首先爆发并选择自己的状态，造成一定的人员伤亡和财产损失，此时突发事件的初始状态信息记为h0。

（2）从t1→t2为T1阶段，应急决策者在t1时刻根据观察到的突发事件初始状态信息h0来判断其状态的概率（先验概率）。在通常情况下，由于初始状态信息h0极度缺乏，因此应急决策者利用自己以往的经验来修正突发事件所处状态的概率（后验概率），然后依据期望效用最大化原则（即风险损失最小化）选择最优的应对方案并进行处置和救灾；同时对突发事件的相关信息进行进一步的收集（记为h1）。

（3）在T1阶段，突发事件随着应急决策者所采用应对方案实施的结果及其自身演化规律，从原来的状态演化为新的状态。

（4）从t2→t3为T2阶段，应急决策者对阶段性救灾成果进行评估，并根据已掌握的新的信息h1和自己对突发事件所处状态的信念进行推断或修正。采用贝叶斯公式计算突发事件状态判断的后验概率，然后依据期望效用最大化原则选择新的最优应对方案进行应急处置与救援。t2→t3为新的应对方案实施时间段；同时对突发事件的状态信息进行收集（记为h2）。

（5）在T2阶段，随着新的应对方案实施，突发事件向另一状态演化，应急决策者又根据收集的信息h2制定最新的应对方案并实施，依次往复，直到突发事件得到有效控制并消除为止。

2 基于信息流的突发事件应急决策模型构建

如上所述，突发事件应急决策过程实质上是应急决策者和突发事件之间的序贯博弈过程，也是应急决策者不断收集事态信息的过程。为了研究方便，假定把突发事件按照时间序列划分为若干个阶段，每一阶段采用一个特定子事件（处于某一特定状态）进行描述，比如天津港“8.12”特大爆炸事故依据时间序列分可为4个阶段，对应的典型子事件分别为：火灾与爆炸事件（记为τ1状态）、环境污染事件（记为τ2状态）、社会稳定与城市安全事件（记为τ3状态）、事故调查与整改事件（记为τ4状态）。基于信息流的应急决策过程为：在进行每一阶段信息收集后，应急决策者需要做出两种决策：一是停止信息收集，以目前所获取的信息为基础预测事件演化态势并制定应对方案，此时实施该应对方案对应一个风险损失值（方案实施风险）；二是继续进行下一阶段信息收集，而信息的收集必然会延误应急决策的制定和实施，这种因时间约束而必须付出的代价被称为信息收集成本，随后求得在期望信息量下最优应对方案的期望风险损失。本文所建模型就是通过对决策风险损失与信息收集成本的比较来制定和评估最优应对方案，从而作为应急决策的依据，其框架模型如图2所示。

图2 基于态势预测的应急决策框架模型

在图2中，表示在第i（i=1，2，…，N）阶段突发事件处于第j状态即为τj（j=1，2，…，J）。

2.1 模型假设

假定突发事件在某一阶段有J种可能状态，把第j状态记为τj(j=1，2，…，J)，对应的最优应对方案记为σi(i=1，2，…，J)。令Pji表示突发事件的实际状态为τj时，应急决策者采取应对方案σi的效用函数，该效用函数采用实施该方案所造成的风险损失（记为Bji）的相反数来度量即：

每一阶段进行信息收集所付出的代价记为Ck(k=1，2，…，N信息收集的样本空间记为{Ii|i=1，2，…，R}（R为样本空间可取值类型），对应的样本值依次记为{hi|i=1，2，…，R} ∈I。对突发事件信息收集的目的就是要预判突发事件的各种实际状态出现的概率，即检验在特定阶段突发事件状态τj为真时，应急决策者采取相应的最优应对方案。

2.2 基于信念修正的应急决策

突发事件发生后，应急决策者凭借其自身经验，一般会对突发事件的状态有一个大致的判断并进行初始应急决策，随着对突发事件状态信息的不断收集和完善，应急决策者需要对先前的判断加以修正，在此基础上制定新的应对方案并加以实施，依次往复，直到突发事件得到有效控制和消除为止。应急决策者利用当前收集到的信息对他先前的判断进行修正通常采用贝叶斯方法[14,15]。应急决策者对突发事件状态的先期判断用概率表示，被称为先验概率，记为：μ(τi)，μ(τ2)，…，μ(τJ)，满足至于先验概率的确定有多种方法[16,17]，比较简单的方法是假定各先验概率服从平均分布（突发事件爆发初期信息极度匮乏时比较适用），比较复杂的方法有最大熵法[18]、边缘分布密度法[19]以及互信息原理[20]等。在应急决策中，突发事件状态的先验概率可根据应急决策者的经验加以确定，特别在突发事件爆发的初期，由于收集到的信息h0严重不足（一般情况下假定为空集即h0=φ），此时可以假设突发事件状态的先验概率服从平均分布。随着处置工作的展开，应急决策者开始收集到突发事件的相关信息h1时，已知条件概率μ(h1|τj)，则突发事件处于j（记为τj）状态的后验概率可以根据如下贝叶斯公式求取：

其中，μ(τj)为突发事件处于j状态的先验概率。

众所周知，应急决策者对突发事件状态信息的收集不是一次性完成的，而是随着处置工作的展开不断收集和完善的过程。为了研究方便，假定把整个应急处置过程也分N个阶段，当信息收集进行到第Tk（k=0，1，2，…，N）阶段时（此时的信息集记为hk），应急决策者可以把第Tk-1阶段确定的后验概率作为第Tk阶段的先验概率，然后按照式（3）确定第Tk阶段的后验概率，在此基础上确定最优应对方案。

式中，μ(τj|hk-1)为应急处置进入第Tk阶段突发事件处于τj状态的先验概率，当k=1时即表示突发事件爆发初始阶段第一次信息收集前的先验概率（初始阶段记为T0阶段，此时假定信息集为空集h0=φ），则有μ(τj|h0)=μ(τj|φ)=μ(τj)，此时式（2）变成了式（3）的一种特殊情况。

在进行突发事件状态信息收集之前，应急决策者对下一阶段收集到的信息是无法确定的，此时需要引入样本空间概率分布的概念。假定样本空间{Ii|i=1，2，…，R} 中各样本的分布概率为μ(I1)，μ(I2)，…，μ(IR)，通常情况下可认为各样本是平均分布的即μ(I1)=μ(I2)=…=μ(IR)=，此时可以根据样本空间概率分布μ(Ii)求出下一阶段信息收集的期望后验概率。令μe(τj|hk)为第Tk阶段信息收集后对第Tk+1阶段进行信息收集的期望后验概率，则有：

2.3 基于风险损失最小化的应急决策

应急决策者在选择救援方案时，不仅仅考虑依据突发事件的状态来确定应对方案概率的大小，而且还要考虑选择各方案时的机会成本即从若干个应对方案中选择一个方案加以实施时，也就丧失了在该种情况下选择其他方案的机会。在应急决策中，由于突发事件的信息收集是一个不断完善的渐进过程，因此在应对方案的选择过程中存在一定程度的风险，在此规定将应急决策者选择某一方案的收益与该状态下（实际状态）选择最优方案的收益之差确定为应急决策者的决策损失（通过决策损失间接反映应急决策者所获得的效用）。根据式（1）界定的决策损失Bji，在信息收集进行了k次后（即应急处置进入第Tk阶段），各个状 态 假 设为真 的 概 率分别 为μ(τ1|hk)，μ(τ2|hk)，…，μ(τJ|hk)，此时采用应对方案σi的决策损失（记为L(hk，σi)）可表示如下：

应急决策者在已收集到的信息范围内采取决策损失最小的方案即选择的应对方案满足下式：

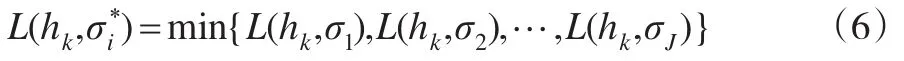
是否需要继续进行信息收集的决策还取决于下一阶段信息收集的预期风险损失以及下一阶段信息收集所付出代价的估计。采用期望后验概率来界定预期决策风险损失（记为Le(hk，σi)）即信息收集进行了k次后在对下一次信息收集结果进行估计的基础上采用应对方案σi的决策风险损失，显然有：

此时应急决策者的预期决策风险损失及其采用的应对方案满足下式：

应急决策者的目标就是通过计算当前阶段的决策风险损失（L(hk，)）与需要下一阶段继续收集信息而做出决策的预期决策风险损失（Le(hk，)）及其继续进行信息收集所付出的代价(Ck+1)进行比较，若满足式（9），则停止进行下一阶段的信息收集，采用当前最优应对方案进行应急处置：

3 实例分析

假定某沿海地区针对即将到来的台风灾害制定了四套应对方案（记为σ1、σ2、σ3、σ4），分别对应台风的四种可能状态：τ1（特别重大）、τ2（重大）、τ3（较大）、τ4（一般）。假定每阶段信息收集付出的代价为1个单位（Ck=1，k=1，2，…，N），样本空间为台风灾害所造成的损失程度即I1（特别严重）、I2（严重）、I3（较重）、I4（一般）。台风灾害各状态与各应对方案所对应的收益矩阵如下页表1所示，根据Bji=max(Bj1，Bj2，…，BjJ)-Bji，(j，i=1， 2，…，J)求得损失矩阵Bji如下页表2所示。

表1 收益矩阵

表2 决策风险损失矩阵

根据以往台风资料统计给出如下判断：

（1）如果台风状态为τ1（特别重大），所造成灾害损失严重程度的概率分别为：

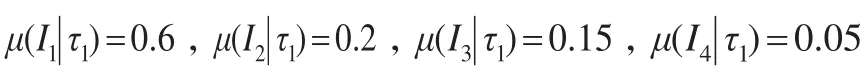
（2）如果台风状态为τ2（重大），所造成灾害损失严重程度的概率分别为：

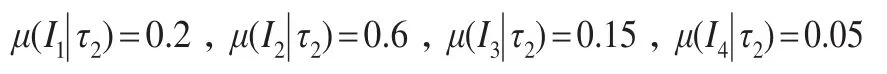
（3）如果台风状态为τ3（较大），所造成灾害损失严重程度的概率分别为：

（4）如果台风状态为τ4（一般），所造成灾害损失严重程度的概率分别为：

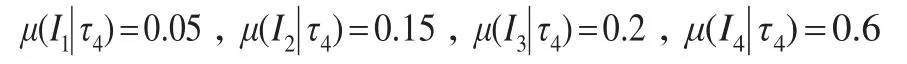
利用所建立模型进行应急决策。分析过程如下：

（1）初始阶段，假定应急决策者没有收集到台风灾害的任何信息（h0=φ）而进行直接决策

此时，首先假定台风的初始状态为等概率分布即μ(τ1|φ)=0.25 ，μ(τ2|φ)=0.25 ，μ(τ3|φ)=0.25 ，μ(τ4|φ)=0.25 ，采用各应对方案（σ1、σ2、σ3、σ4）的风险损失计算如下：

①当采用应对方案σ1时，其风险损失为：

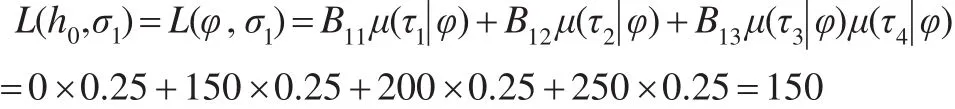
②当采用应对方案σ2时，其风险损失为：L(h0，σ2)=L(φ，σ2)=162.5

③当采用应对方案σ3时，其风险损失为：L(h0，σ3)=L(φ，σ3)=212.5

④当采用应对方案σ4时，其风险损失为：L(h0，σ4)=L(φ，σ4)=300

从上述计算可知：L(h0，σ*i)=min{L(h0，σ1)，L(h0，σ2)，L(h0，σ3)=L(h0，σ1)=150，此时应急决策者最好采用应对方案σ1。

（2）进行第一阶段的灾害信息收集（h1）

此时假定各灾害造成的损失程度是等概率的即μ(I1)=μ(I2)=μ(I3)=μ(I4)=0.25 ，则各自的期望后验概率为：

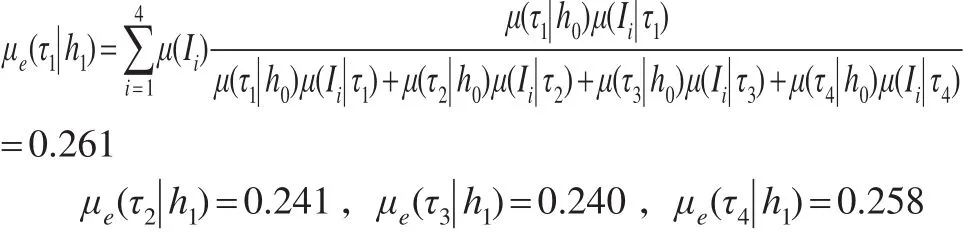
此时采用各应对方案（σ1，σ2，σ3，σ4）的期望风险损失计算如下：

①当采用应对方案σ1时，其期望风险损失为：

②当采用应对方案σ2时，其期望风险损失为：Le(h1，σ2)=165.9

③当采用应对方案σ3时，其期望风险损失为：Le(h1，σ3)=215.4

④当采用应对方案σ4时，其期望风险损失为：Le(h1，σ4)=298.9

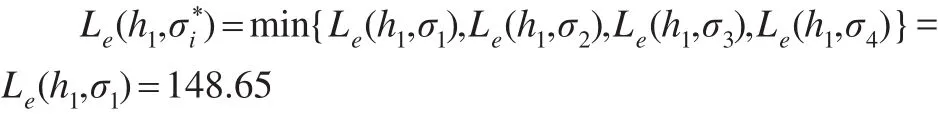
（3）L(h0，σ1)=150＞Le(h1，σ1)+C2=149.65 即应急决策者不收集信息而直接采用应对方案σ1所造成的风险损失要比进行第一阶段信息收集再采用σ1所造成的期望风险损失要大，故应急决策者应该进行第一阶段的信息收集，这说明应急决策者所拥有的事态信息不足，可能导致决策的准确性偏低。

（4）假设第一阶段收到的灾害损失结果为I1（信息收集h1的结果表明灾害特别严重）时，这时实际的后验概率为：

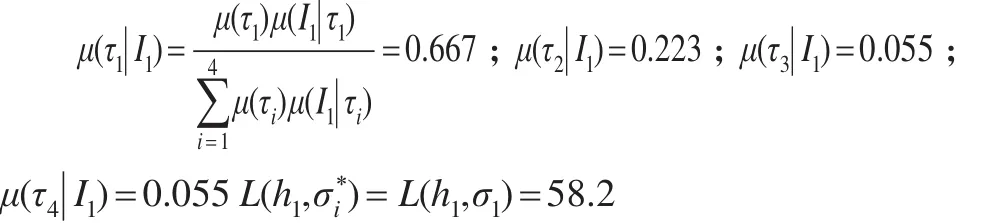
（5）假设进行第二阶段的灾害信息收集（h2），期望后验概率为：

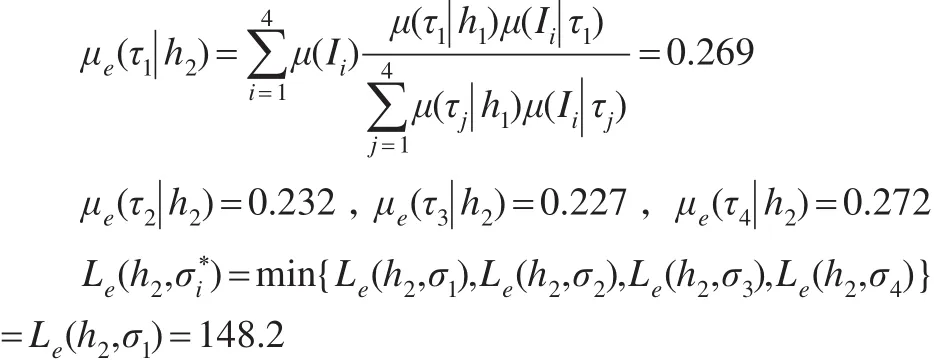
由于L(h1，σ1)=58.2≺Le(h2，σ1)+C2=149.2 ，故应急决策者不需要进行第二阶段的信息收集而直接进行决策选择，这也说明过度的信息收集会延误决策，由此会导致更大的灾害损失。

综上分析，应急决策者的应急决策过程为：当台风灾害来临时，应急决策者根据以往台风资料统计和自身经验判断，可以直接启动应对方案σ1，此时的风险损失最小；然后应急决策者进行第一阶段的信息收集，如果此时收到的灾害信息h1表明灾害特别严重（I1），则可以预测此次台风灾害的态势为特别重大（τ1），继续采用应对方案σ1进行应急处置和救援，此时应急决策者的效用最大，处置效果最好。

4 结束语

非常规突发事件具有突发性、动态性、不可预测性、深度危害性等一系列特殊属性，这就要求应急决策者必须在环境复杂、时间紧迫、信息缺失和压力巨大的特殊背景下快速制定应对方案并加以实施，然而现实情况不允许应急决策者随心所欲地随便决策（责任追究），需要在简单分析工具的支持下制订科学合理的应对方案。博弈论作为一种简单的决策分析工具，为该问题的解决提供了新的途径。首先阐述应急决策过程实质上是一个应急决策者和突发事件间的序贯博弈过程，随后从序贯博弈的视角构建了基于信息流的应急决策模型，在对突发事件的演化态势进行预测的基础上制订应对方案。最后的算例分析说明了危机情景下应急决策的质量依赖于应急决策者对事态信息收集和掌握的程度。过度的收集信息会延误决策，而信息收集不足又会影响决策的精确性，二者势必都会造成更大的灾害损失，因此应急决策者对信息收集要掌握适度原则。另外，算例分析也验证了所建模型的有效性和可行性。