Review of Methods of Image Segmentation Based on Quantum Mechanics

Tian-Chi Zhang | Jing Zhang* | Jian-Pei Zhang | He Wang

Abstract—The quantum theory application is a hot research area in recent years, especially the theory of quantum mechanics. In this paper, we focus on the research of image segmentation based on quantum mechanics. Firstly,the theory of quantum mechanics is introduced; afterwards, a review of image segmentation methods based on quantum mechanics is presented; and finally, the characteristics about the quantum mechanics applied to image processing are concluded. Two main research topics are discussed in this paper. One is to emphasize that quantum mechanics can be applied in different research areas, such as image segmentation, and the second is to conclude some methods in image segmentation and give some suggestions for possible novel methods by applying quantum mechanics theory. As a summary, this is a review paper which presents some methods based on the feasible theory in quantum mechanics aiming at achieving a better performance in image segmentation.

1. Theory of Quantum Mechanics

1.1. Quantum Mechanics Research History

Quantum mechanics is also called as quantum physics or quantum theory. It is a subset of physics in micro level that explains the behaviors at the molecular, atomic, and sub-atomic levels. On the contrary, classical physics only explains the matter and energy on the macro scale. However, scientists have discovered the phenomena in both the macro and the micro worlds that classical physics could not explain[1]. Coming to terms with these limitations led to the revolutions in physics, which created the development of quantum mechanics[2].

Quantum mechanics is a mysterious key that suggests that we can use quantum to interpret the present and future world. The mystery of quantum is in its state, such as the quantum entangled system, which includes supersymmetric string, quantum entanglement, superposition, and wormhole.

A quantum entangled system is defined to be one whose quantum state is not individual particles but is an inseparable whole. In entanglement, one particle cannot be fully described without considering the rest. Note that the state of a quantum system is always expressible as a sum, a string, or a superposition of products of states of local particles; it is entangled if this sum necessarily has more than one term. Quantum systems can become entangled through various types of interactions. Entanglement is broken when the entangled particles decohere through interaction when a measurement is made. Until today, researchers still do not know why quantum mechanics is so mysterious, but the mainstream of research areas has accepted the particularity of the objective existence of supersymmetric string, quantum superposition, quantum entangled states, and wormhole which are considered to be the most powerful theory.

The history of quantum mechanics theory is as follows. In 1968, Veneziano[3]discovered a simple analytic formula that exhibits duality with linear Regge trajectory, which is given by a sum of ratios of Euler gamma functions. The formula describes scattering amplitudes in the tree approximation to a consistent quantum theory.Very soon after the appearance of the amplitude, in 1969, Virasoro[4]proposed an alternative formula which has similar virtues. Since this formula has total symmetry, it describes particles that are singlets of the Chan-Paton symmetry group. In 1970, Gross et al.[5]discovered unanticipated singularities in a particular one-loop diagram. In 1974, Wess and Zumino[6]formulated a class of 4 dimensional (4D) supersymmetric theory, which was motivated by the search for 4D analogs of the 2D world-sheet action. They launched the study of supersymmetric field theory,which proceeded in parallel with the development of supersymmetric string theory. At the same year, Scherk and Schwarz proposed to interpret the string theory as a unified quantum theory of all forces including gravity. This is the first time that the string theory appeared in the quantum theory. In 1982, Green and Schwarz[7]manifested the space time supersymmetry of the Gliozzi-Scherk-Olive (GSO)-projected Ramond-Neveu-Schwarz (RNS) string;they classified the consistent ten-dimensional superstring theories and gave them the names: Type I, Type IIA, and Type IIB. In 1985, they also showed that the spinor state SO(32) is the unique choice for the cancellation occuring.They decided to explore the low-energy effective field theory to see whether the gravitational and mixed anomalies also canceled[8]. In 1995, Witten proposed the M-theory[9]. Based on Witten’s results, Green et al. and Schwarz have verified that all gauge, gravitational, and mixed anomalies do in fact cancel for the gauge group SO(32)[10],[11].In 1997, Banks et al.[12]proposed the matrix theory to describe the M-theory. In 1998, Maldacena[2]pointed out that the high degree of gravity theory or superstring theory, equals to the low degree of gauge field theory, that is, the superstring theory was firstly presented. In 2002, Berenstein et al.[13]explained how the string spectrum in flat space and pp-waves arises. In 2004, Arutyunov et al.[14]proposed the Bethe equations for the diagonalization of the Hamiltonian of quantum strings at large string tension and restricted to certain large charge states. They also showed that their ansatz quantitatively reproduces everything that is currently known about the string spectrum of these states. In 2008, Silverstein and Westphal[15]presented a simple mechanism for obtaining large-field inflation,and hence a gravitational wave signature, from the string theory compactified on twisted tori. In 2012, polarization correlation was created between photons that never coexisted in time. The result was achieved by entanglement swapping between two pairs of entangled photons after measuring the polarization of one photon of the early pair,which proves that quantum non-locality applies not only to space but also to time[16]. Up to 2012, quantum entangle was founded. In 2013, it was shown that classically communicated separable quantum states could be used to carry entangled states[17]. In 2014, a Brazilian researcher, Lemos, was able to “take pictures” of objects using photons that had not interacted with the subjects, but were entangled with the photons that did interact with such objects[18]. Lemos, from the University of Vienna, is confident that this new quantum imaging technique could find applications where low light imaging is imperative, in fields like biological or medical imaging. In 2016, Abbott et al.[19]detected gravitation which is a great breakthrough in basic physics in the theory of quantum mechanics.

As a summary, the different works described have made important contributions to the development of quantum mechanics theory; especially, have proposed string, superstring, quantum entangle, and the existence of gravitational waves. In addition, the quantum theory, especially string and quantum entanglement, has not only been experimented, but also been put forward with the described formula.

1.2. Principle and Formula of Quantum Mechanics

In the over 40-year history, the quantum theory is perhaps the best candidate to provide a physic and other field theory. The only assumption is that all what surrounds us is composed of tiny vibrating and entangling strings instead of the point like particles[20]. Surprisingly, this relatively simple assumption that originally attempted to address the physics of the strong interactions turns out to yield a quantum theory of gravity. The quantum theory is formulated in various special mathematical formalisms, such as, the string vibrating, Kaluza-Klein (KK) modes, and quantum entangle measure.

A. String Vibrating

String vibrating looks like the movement of pendulum, as shown in Fig. 1. The equipment of pendulum includes the center of the disc with mass m1, which is connected with a straight rod with a mass of m2, and its radius is a.The other end of the rod is fixedly connected with the center O of a hollow cylinder with a radius of b, and the rod length is l=b-a. The disk vibrates around the point O.

Fig. 1. Equipment of pendulum.

The movement equations are as follows. The kinetic energy of the rod is

The rotation angle of the disc is bθ=a(θ+φ), it equals to the angle sum of cylinder θ and disc φ. The rotational kinetic energy of the disc around the point O is

The equipment takes the point B as the standard potential energy V, and the system’s kinetic energy T as

Bring (3) and (4) into string vibrating equation (5):

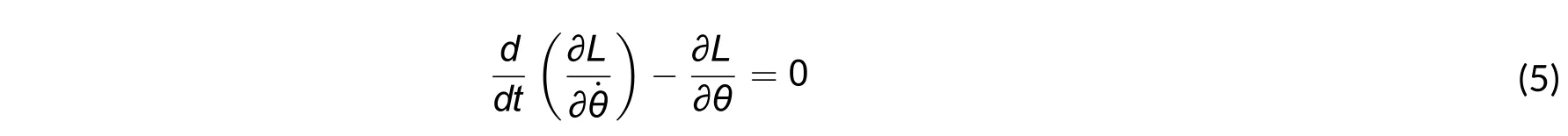
where L=T+V, and then we obtain

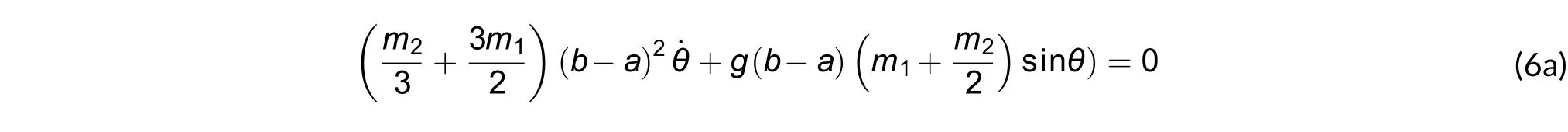
or

Equation (6) shows that string vibrating can be presented by a formula described by sinθ, its vibrating is a string which moves in the form of a sine wave.B. Kaluza-Klein (KK) Modes

With the development of string theory, we know that string also can be in the form of D-branes. Kaluza and Klein taught us that the 4D matter particles appearing in the effective theory have some heavier “cousins”dubbed Kaluza-Klein (KK) modes[21],[22]. The KK modes arise from the components associated to the compact coordinates. Taking the example of an additional dimension compactified on a circle of radius R, a scalar field φ=φ(xµ, ζ) can be expressed as

Some of the essential features of moduli stabilization are captured in the so-called KKLT model. The KKLT model is described as follows. After fixing the moduli, the fluxes render a constant contribution W0to the superpotential. In this ideal setup, the dilaton has acquired a mass and all tadpoles have been canceled. A Kähler moduli T, only the overall volume moduli, is left untouched and thus the string coupling depends only on this moduli. The result is the super-potential:

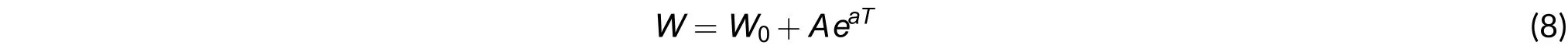
Together with the tree-level Kähler potential, the scalar potential is

This scalar potential is always negative, it must be pointed out that the moduli T has been stabilized. Therefore,from (9) we know the string theory can be represented by the exponential function.C. Quantum Entangle Measure

The quantum entangle measure provides an important clue for developing a description of quantum entangle,which is that the related phenomena of entanglement and wormholes might in fact be equivalent.

The probability density function of Q(y) of quantum state of each particle y is described as

where, N=h2/mγ, γ is the intensity of the potential well, m means the particle mass, and h is the Planck’s constant. When a particle moving towards the potential well’s center, the quantum state function Q(y) portrays the location of a particle probabilistically. Therefore, the estimated position of the particle can be obtained by

where L is the characteristic length of the potential well and μ indicates the random digital between 0 and 1,which means the distance between particles in quantum entangle is decided randomly. Pidis the ith components of the personal best (pbest) position of the particle. Supposed, the particle’s P of coordinates is

If the random digital μ＞0.5,

If the random digital μ≤0.5,

where α is the expansion coefficient of contraction, it controls the convergence speed. And, where tmaxrepresents the maximum number of iterations.

Totally, we found that the three formulas of string vibrating, KK modes, and quantum entangle measure all include exponential formula, and they have some relationships with a lot of possibilities in describing the secret of nature. We hope the theory formulas have gone from a theory of quantum mechanics to a theory of everything. We predict that a successful string and entangle model should be able not only to reproduce the particle physics of our universe, but also to explain the structure and dynamics of the mysterious key in the problems that we cannot solve[23], such as, in the mysterious principle and process in image segmentation.

2. Research and Methods

The recent developments in quantum information processing indicate that exploiting the immense potential of quantum computer systems can have a revolutionary impact on the field of computer science. This is due to the immense computing power provided by a quantum machine compared with that of a classical one. Quantum is a mysterious key that we can use quantum to interpret the future world. The mystery of quantum is in its state, such as quantum entanglement, superposition, and wormhole. When a quantum state changes, another quantum immediately follows the reverse no matter how far apart. And the quantum entanglement and superposition are led by wormhole to other place immediately no matter where and how far away. Until today, people still do not know why quantum behaves in such a mysterious manner, but the mainstream of the international community has accepted the particularity of the objective existence of quantum superposition, quantum entangled states, and wormhole based on that the application of quantum information is considered to be the most powerful.

In the image segmentation research area, there is an increasing number of people experimenting with the theory of quantum mechanics aiming at looking for novel methods to achieve accurate and efficient results.

2.1. Quantum Mechanics Theory for Image Segmentation

We can divide these methods into two groups. One group is the direct application which proposes new methods using the quantum mechanics theory. The other group uses the quantum mechanics theory combined with existing methods, such as the quantum theory combined with particle swarm optimization (PSO), called QPSO, combined with the genetic algorithm (GA), called QGA, and combined with the support vector machine(SVM).

The direct application of quantum theory includes the two-state quantum system, quantum elitist frogs, SVM kernel defined by the quantum state, quantum permanents, quantum collapse models, quantum entanglement criteria, entanglement quantum measures, and generation and evolution of entanglement, etc. Youssry et al.[24]applied the quantum theory of the two-state quantum system to the problem of foreground image segmentation.They treated each individual pixel as a particle. The number of states was corresponding to the foreground and background of the image. As the use of the two-state quantum computing systems, Caraiman and Manta[25]investigated on histogram-based image processing operations and developed quantum algorithms for histogram computation and threshold-based segmentation. In addition, Venegas-Andraca and Ball[26]briefly explored potential experimental realizations by using maximally entangled states. Different from that image reconstruction requires not only the storage of light parameters but also additional information like correlation and pixel spatial disposition, they showed that the employment of maximally entangled qubits allows reconstructing images without using any additional information. Their proposal could be employed to enable emergent quantum technology to be used in high-impact scientific disciplines in which extensive use of image processing has been made. Besides, Ding et al.[27]applied the theory of quantum elitist frogs to segment images. They proposed a more efficient algorithm by combining quantum elitist frogs and cloud model operators (QECMASCR). Some optimal elitists in different memeplexes of multilevel elitist pool were selected out and applied into magnetic resonance imaging (MRI)segmentation, and the effective and robust segmentation results had been obtained. As for the application of quantum permanents, Gurvits[28]used it to solve the Edmonds problem. His algorithm is a thoroughgoing generalization of algorithms, and its analysis benefits from an operator analog of permanents quantum permanents.For the theory of quantum collapse models, Reintjes and Bashkansky[29]investigated the extent of it to predict if propagation properties agree with the predictions of non-collapse models. Besides the theory above, Terhal[30]reviewed the criteria for quantum entanglement, both in a bipartite setting and in a multipartite setting. He discussed the Bell inequalities, entanglement witnesses, entropic inequalities, bound entanglement, and several features of multipartite entanglement. Fang and Chang[31]clarified the relationship and physical implications of different measures of entanglement and quantum particle correlation in a system containing indistinguishable particles.

As for the quantum mechanics theory combined with existing methods, many researchers combine the quantum theory with GA. For example, Isar[32]used the Peres-Simon necessary and sufficient criterion for the separability of two-mode Gaussian states. He described the generation and evolution of entanglement in terms of the covariance matrix for a Gaussian input state. Mo et al.[33]used hybrid quantum genetic algorithms (HQGA) to optimize the parameters of SVM. HQGA combined with the excellent global optimization capability of QGA and the excellent local optimization ability of gradient descent (GD) gives a better solution to the traditional problem on parameter optimization of SVM. In addition, some researchers combined the quantum theory with SVM, such as Wang et al.[34]who used the quantum state of uncertainty to define the kernel in SVM. Classification experiments showed that the convergence speed is fast and the rate of accurate recognition is high. Anguita et al.[35]considered the application of quantum computing to solve the problem of effective SVM training, especially in the case of digital implementations. In addition, Yuan et al.[36]applied the qubit state theory to adaptive median filtering algorithm. The quantum signal algorithm framework is firstly to transform the input image into qubit state representation. Secondly the quantum measurement outcomes are obtained based on quantum measurement postulate. Thirdly the quantum measurement outcomes are transformed into the algorithm outcomes. About the quantum theory combined with PSO, Yu et al.[37]analyzed it with the traditional maximum entropy thresholding algorithm, and combined with PSO into the quantum behavior of PSO. Shabanifard and Amirani[38]introduced a modified cooperative method, cooperative-Gaussian-quantum-behaved PSO (CGQPSO), based on Gaussianquantum-behaved PSO (GQPSO). Gao et al.[39]proposed the cooperative method (CQPSO) which preserved the fast convergence rate of PSO and employed the quantum-behaved PSO to save computation time and to conquer the curse of dimensionality.

The above methods benefit from the theory of quantum and are concluded in the following fields: 1) the Hamiltonian operator and the solution of the evolution equation, which simulated the procedure of the theory to analyze the process of segmentation; 2) maximally entangled states, which are employed to enable emergent quantum technology to be used in high-impact scientific disciplines; 3) maximally entangled qubits or quantum elitist frogs and cloud model operators, which apply the method to image segmentation. 4) using the quantum state of uncertainty to define the kernel in SVM; 5) using the principle of quantum bit and superposition of states to propose a novel evolutionary algorithm; 6) using some concepts, such as entropy or Gaussian, to the modified method of QPSO.

Can we apply the quantum theory to the existing methods or create new methods of image processing based on the quantum theory? Is there any quantum theory similar to quantum theory above applied to image segmentation? The answer is “yes”. We found a research from Maldacena who is a theoretical physicist at the Institute for Advanced Study in Princeton, in quantum gravity and string theory research where he made important contributions, and won the Breakthrough Prize in Fundamental Physics in 2012. “Entanglement and wormhole seemingly unrelated that quantum entanglement and the wormhole may be equivalent to: Black holes, and small particles, entangled objects may by wormholes connect,” he said[40]. That is, the wormhole has the similar principle with entanglement. Can we apply the wormhole theory to image segmentation? In addition, the Bose-Einstein condensate (BEC) is a quantum state of matter of a dilute gas of bosons cooled to the temperatures very close to the absolute zero, and a large fraction of bosons occupy the lowest quantum state, at which point microscopic quantum phenomena, particularly wavefunction interference, become apparent[41]. BEC includes three states: The state of just before the appearance of a Bose-Einstein condensate, state of just after the appearance of the condensate, and state of after further evaporation, nearly the pure condensate. Can the BEC states be applied to image processing similar as the two-state quantum system? Yes, related research has been done and the solution is that the BEC theory can inspire us to improve the kernels in traditional artificial algorithms, such as, a novel BEC kernel modified based on the SVM kernel.

2.2. Charcteristics of Image Processing Based on Quantum Mechanics Theory

The existing methods explained the above simulated, analyzed, employed, or applied the quantum entanglement theory or principle aiming to achieve a better performance in the area of image segmentation. It should be noted that quantum mechanics only provides the framework and the general discipline that methods obey. However, it does not specify the details about particular applications. For example, the theory does not specify exactly the form of the Hamiltonian operator for different methods. This is considered a powerful point in the theory, since it provides a generic platform that could be used to address issues in diverse disciplines. In this case,the selection of the framework elements could be adapted, and consequently, the general rules of quantum mechanics could be applied to solve a particular problem.

Quantum-based image segmentation is characterized by the use of a “quantum-inspired” computational method which is inspired by certain principles of quantum mechanics and the use of a classical algorithm for checking that the “candidate” solutions generated by the quantum-inspired computational method are in fact correct. Thus, quantum mechanical computational methods can be classified into two fields. One concentrates on generating new quantum algorithms using automatic programming techniques. The other concentrates on quantum-inspired evolutionary computing for a classical computational method, a branch of study on evolutionary computing that is characterized by certain principles of quantum mechanics.

There are some specific image segmentation approaches that may be used. Besides the existing applications of quantum theory in image segmentation, there is still some other quantum theories, such as string vibrating and wormhole to be studied or be used. In addition, we may not only apply the principle and formula of the quantum theory in this paper, but also can find more quantum theories, such as, BEC to benefit the shape or process of it to design or predict the object shape in image segmentation.

3. Conclusion

This paper is not only a review on quantum mechanics theory applying to image segmentation methods, but also proposes that there are some relationships among the quantum theory formulas and among the quantum theories. Pointing out the exponential formula among the three formulas of string vibrating, Kaluza-Klein (KK)modes, and quantum entangle measure seems to have a lot of possibilities in describing the secret of nature,including the mysterious principle in image segmentation. As for the quantum theory, we put forward that the theory of wormhole and BEC may be used in the image segmentation method in near future.