云环境下基于运算电路的同态认证方案
白 平,张 薇,王绪安
(1.武警工程大学 密码工程学院,西安 710086; 2.武警工程大学 信息安全保密重点实验室,西安 710086)
0 引言
随着云计算技术[1]的不断发展,利用 “云端”存储数据越来越受到广大用户的青睐;与此同时,外包给 “云端”的数据如何确保其安全性和可靠性同样引起了人们的关注。目前,对于外包数据的安全性已经通过各种加密方式[2]进行了有效的解决。然而,如何对外包数据的计算结果进行有效验证仍是当前比较棘手的问题,见文献[3-5]。本文的研究重点也是侧重于如何进行外包数据的验证。考虑如下一个具体的应用环境:假设用户把数据m1,m2,…,mn外包给“云端”进行存储,随后用户想要 “云端”对这些数据进行某种运算如R(m1,m2,…,mn) →m。存在的问题是用户如何确保云服务器能够正确执行计算指令呢?一个最直观的方法是云服务器把这些数据回传给用户,由用户自己计算,然后与服务器计算的结果进行对比。这种方法虽然简单却极大地削弱了外包的价值,增加了用户的开销花费。此外,由于不同的服务器提供不同的服务功能,用户可能会在服务器之间进行数据传输以保证用户利益最大化,但是服务器是一个不可完全信任的机构,用户数据可能会因为各种原因被恶意篡改甚至丢失,给用户带来了极大的安全隐患,这就迫切需要去寻找一个安全高效的机制来完成外包计算的验证以及用户数据在不同服务器传输过程中的完整性。
同态消息运算认证(Homomorphic Message AuthentiCator, HomMAC)最初由Gennaro等[6]提出。相比其他验证方法如PDP(Provable Data Possession)[7],同态消息运算认证具有两个独特的优点:1)允许任何人在不知道私钥的情况下认证待验证的消息;2)允许拥有私钥用户在不知道原始输入情况下验证计算结果的正确性。
该方案将同态解密思想(homomorphic decryption)运用到Catalano等[8]提出的基于算术电路实用同态消息认证方案中,构造了云环境下基于运算电路的同态认证方案。相比文献[8],方案在复杂度上有所增长。然而,本方案可以进行任意次乘法同态而不会增大验证标签大小,实现了更高效的同态认证。另外,可以提供不同服务器之间数据完整性和有效性的验证,增强了用户外包数据的安全性。同态消息认证允许用户在不知道私钥情况下对数据消息进行验证,从而很大程度上方便了用户。随着同态认证受到越来越多的关注,涌现出了许多这方面研究成果[9-11]。
1 预备知识
1.1 标签函数
标签函数(labeled program)由Gennaro等[6]提出。标签函数定义为P=(f,τ1,τ2,…,τn),其中f:Mn→M是运算函数,τ1,τ2,…τn∈{0,1}*是二进制串。在标签函数P1,P2,…Pt和函数g:Mt→M已知情况下,标签函数也可表示为P*=g(P1,P2,…,Pt)。文献[6]的方案中限制了标签函数在布尔电路f:{0,1}n→ {0,1}中,本文方案中将其扩展到运算电路中,为f:Mn→M。
1.2 同态消息运算认证方案
同态消息运算认证(HomMAC)方案主要由4个算法构成,具体如下。
KeyGen(1λ) 输入安全参数λ,输出私钥sk和解密密钥ek。
Auth(sk,τ,m) 输入私钥sk,消息m∈Μ和对应消息标记τ,输出验证标签σ。
Ver(sk,m,P,σ) 输入私钥sk、消息m、验证标签P=(f,τ1,τ2,…,τn)和标签函数P=(f,τ1,τ2,…,τn),则验证结果正确时输出为1;反之,输出为0。
Eval(ek,f,σ) 输入解密密钥ek,运算电路f:Mn→M和验证标签向量σ=(σ1,σ2,…,σn),输出新验证标签σ。
1.3 半诚实模型

定义1 半诚实模型:设g=(g1,g2)是确定性函数,如果存在多项式时间的方案Sim1和Sim2,即:
那么协议η在静态半诚实敌手A存在情况下是安全的计算函数g。
1.4 同态解密
同态解密方法被广泛应用于降低噪声的各种场景中。当进行同态密文乘法运算时,密文大小会被迅速放大,从而制约了密文操作次数,影响了同态效率。在实际云数据传输过程中,需要对传输数据进行验证。然而,验证标签的大小会随同态乘法运算被放大,影响验证的效率。在本方案中,对同态乘法运算后的密文作同态解密操作,则可以将验证标签的大小降低到接近初始状态时的大小,从而达到任意次密文运算的目的。方案中设置了如图1所示的电路,该电路中包含一个加密电路和一个解密电路,输入到该电路的多项式验证标签运用某种算法协议进行一系列的加解密操作后可以降低多项式验证标签的次数。为了便于进行下一次运算,还在电路中增加一个门电路,统称为增强验证电路Ω。
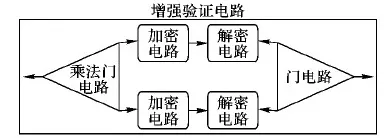
图1 增强验证电路示意图
2 安全模型、结构模型及实例模型分析
2.1 云环境下基于运算电路的同态认证方案安全模型
在同态消息运算认证(HomMAC)中,敌手A和挑战者B进行博弈游戏,具体游戏HomUF-CMAA,HomMAC(λ)过程如下:
Setup 挑战者B运行KeyGen(1λ)获得了私钥sk和解密密钥ek,而后发送解密密钥ek给敌手A,同时,初始化列表T=∅。
Tag queries 敌手A不间断地询问消息标记τ,具体分以下三种情况:1)假如敌手A发送重复询问(τ,m)∈T给挑战者B,则挑战者B发送相同的答复。2)假如敌手A发送询问(τ′,m)∈T给挑战者B,即用同一个标记τ标记了两个不同消息m和m′,则挑战者B忽略此询问。3)假如敌手A发送询问(τ,m)∉T给挑战者B,则挑战者B运算TagGen(sk,τ,m)生成新的验证标签σ← TagGen(sk,t,m),同时更新T=T∪(τ,m)。
Verification queries 敌手A发送询问(m,P,σ)给挑战者B,挑战者B运用Ver(sk,m,P,σ)进行验证,输出结果为1或者0。
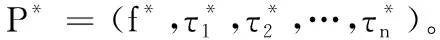
1)伪造1:P*不是定义在T上。
2)伪造2:P*定义在T上,但是m*不是正确的输出,即m*≠f*({mj}(τj,mj)∈T)。
若上述游戏概率可表示为Pr[HomUF-CMAC,HomMAC(λ)=1]≤ε(λ),其中ε(λ)是一个可忽略的函数,则可以判定该同态认证方案是安全的。
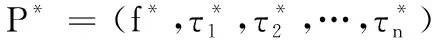


2.2 云环境下基于运算电路的同态认证方案结构模型
当两个多项式验证标签σi(i=1,2)进行同态乘法运算时,首先会输入到一个乘法门电路中,经过乘法门电路的作用后,验证标签的大小会被迅速放大。为了降低验证标签的大小,将其结果输入到增强验证电路Ω中,通过增强验证电路中加密电路和解密电路的共同作用,输出新的密文验证标签大小会接近于一个新鲜密文大小,从而保持了验证标签的大小在低水平范围内。反复递归此过程,则可以达到任意次密文运算的目的。
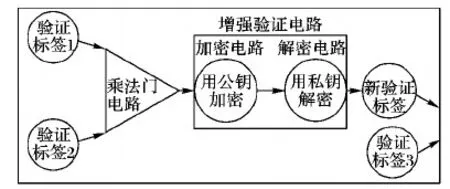
图2 方案运行模拟示意图
2.3 云环境下基于运算电路的同态认证方案实例模型
云环境下外包数据的存储主要由三种实体结构组成:普通用户、云服务器、可信第三方。
普通用户 数据存储计算能力相对较弱,倾向于把一些复杂的数据资源交给云服务器来存储或者计算,但希望这些数据不能被云服务器窃取或者篡改。
云服务器 有大量的存储和计算能力,能为用户提供云存储和计算服务,但是云服务器上的数据可能会遭受黑客的恶意攻击,所以必须对存储数据进行验证以确保安全性。
第三方 作为用户与云服务器的中间媒介,第三方(Third Party Administrator, TPA)将得到的最终结果反馈给事先指定用户,确保传输数据的安全性。
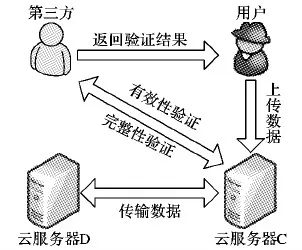
图3 传输数据实例模型
3 云环境下基于运算电路的同态认证方案
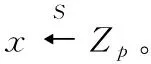
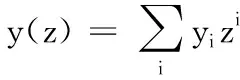
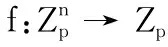
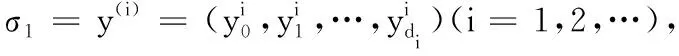
1)同态加法运算。取d=max(d1,d2),则通过计算y(z)=y(1)(z)+y(2)(z),得到新多项式验证标签σ的系数为(y0,y1,…,yd)。
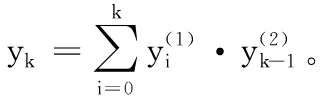
3)带变量的同态乘法运算。取d=di(i=1,2),另一个标签为变量c,则通过计算y(z)=c·y(1)(z),得到新多项式验证标签σ的系数σ=(y0,y1,…,yd)。
Homomorphic_decryption(σ,pk,skv) 将GateEval(ek,g,σ1,σ2)生成的新多项式验证标签σ输入到增强验证电路Ω中,利用公钥pk对新验证标签σ进行加密,而后输入解密电路中用私钥skv进行解密,该解密电路输出的密文相当于一个新鲜密文,它的大小会远远小于之前的密文大小。
Ver(sk,m,P,σ) 定义P=(f,τ1,τ2,…,τn)为标签函数,验证标签为σ=(y0,y1,…,yd)以及m∈Zp。具体验证过程如下:
1)如果y0≠m,则返回0;否则进行下一步。
2)令消息标记为τ,计算γτ=FK(τ)。
3)对步骤2)中的每一个γτi(i=1,2,…,n),计算f(γτ1,γτ2,…,γτn) →ρ。而后运用x计算如下等式是否成立:
(1)
若为真,则输出为1;否则输出为0。
4 方案的分析
4.1 安全性分析
本方案的安全性依赖于同态认证的安全性以及增强验证电路Ω的安全性。同态认证的安全性可以利用Schwartz等[12]方案中的命题1进行证明,增强验证电路的安全则可以在半诚实模型下得以证明。
命题1 令λ,n∈N,Π表示阶为q的有限域M上的运算电路f:Mn→M的集合,其中电路f的深度最大为d且有d/q<1/2。可以得出如下推断:对于f∈Π存在这样的概率算法:∀μ∈Mn,y∈M使得f(μ)=y的概率至少为1-2-λ。
定理1 如果F是一个伪随机函数,则方案的同态消息认证是安全的。
为了证明方案的正确性,定义一个由敌手A执行的实验游戏Gi(i=1,2,…,4),并最终输出1。
游戏G0输入验证询问(m,P,σ),为了辨别标签函数P是否被定义在T上,挑战者B使用命题1进行概率测试,则任何敌手A进行Q次验证询问后可得到如下不等式:
‖Pr[HomUF-CMAA,HomMAC(λ)]-Pr[G0(A)]‖≤
Q·2-λ
(2)
游戏G1同游戏G0中的博弈类似,所不同的是游戏G1中所用的是真正随机函数R:{0,1}*→Zp,并随机产生γτ∈Zp。
游戏G2首先,对于所有验证询问(m,P,σ=(y0,y1,…,yd)),如果y0≠m则输出为0。其次,对于所有的验证询问(m,P,σ),如果P不是被定义在T上,则挑战者B执行以下步骤:
1)对于每一个τi,如果(τi,·)∉T,则计算γτ1←R(τi)。
2) 使用算法Ver(sk,m,P,σ)计算ρ的值。

游戏G3对于所有验证询问(m,P,σ),其中P=(f,τ1,τ2,…,τn)定义在T上,挑战者B执行以下操作:


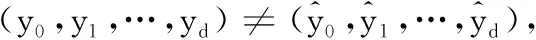
游戏G4设定bad是表示“false”的一个标识符,当挑战者B接收到验证询问(m,P,σ)后,如果满足以下两个条件:
1)按照验证询问(m,P,σ)的要求,挑战者B计算出了Z的值。
2)计算的输出为Z=0 modp,则挑战者B输出1,并且设定bad → True。
定义bad4表示游戏G4中bad → True事件,由于所有伪造的验证询问只能是游戏G3中的1)或者2),故任何敌手赢得游戏G4的概率为0,即Pr|G4|=0。
为了证明定理1,需要证明以下引理:
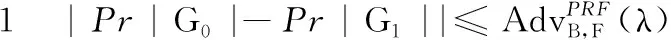
引理1的证明类似于伪随机函数的安全性证明。
引理2 Pr|G2|≡Pr|G3|

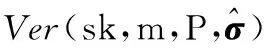
引理3 Pr[G3]-Pr[G4]≤Pr[Bad4]
如果事件Bad4在游戏4中发生,挑战者B可能会对某些验证询问提供不同的回应,因此,有Pr[G3]-Pr[G4]≤Pr[Bad4]。

证明 对于j=1,2,…,Q,令Bj表示这样一个事件:敌手A询问了j次之后使得bad → True,则可以得出如下结论:
(3)
其中:证明的关键之处在于Pr[Bj]的概率由挑战者B随机选择的变量x、参数γτ和敌手A随机选择的参数所评估代替。
定义(m,P,σ)表示第j次验证询问,根据P是否定义在T上,Bj有以下两种可能性:
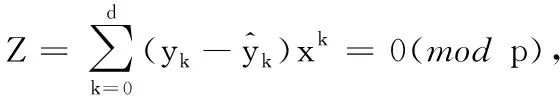
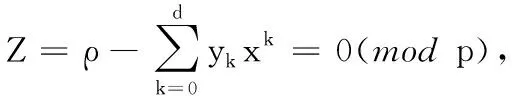
Pr[Bj]=Pr[Zj=0|Z1≠0∧Z2≠0∧…∧Zj-1≠0]
(4)
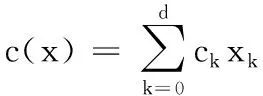
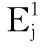
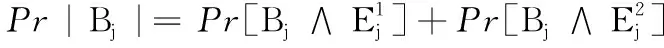
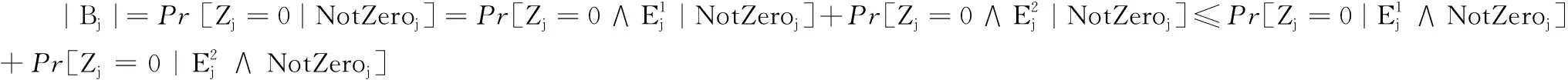
(5)
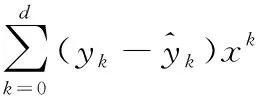
(6)
(7)
最后,将式(6)和(7)运用到式(5)中可推导出如下不等式:
(8)
进而可以得到上限值:
(9)
综上所述,可以证明定理1:
(10)

本方案中增强验证电路的安全性建立在半诚实模型下,参与方(真实方和模拟方)诚实的执行相关算法协议,假设真实方与模拟方分别拥有多项式向量集合M*=(M1,M2,…,Mn),S*=(S1,S2,…,Sn),模糊匹配的操作对象就是针对M*和S*中的某两个多项式向量进行作用。
在方案证明过程中为了标识方便,将直接使用M和S作为向量,假设真实视图中对向量M输出为BFM,模拟视图中对向量S输出为CFS,将BFM和CFS进行作用产生交集BCFM∩S,记录交集中匹配成功的个数。如果个数大于或者等于事先设定的门限值t,则真实视图和模拟视图具有不可区分性,反之,二者可区分。
定理2 设M、S分别是预定义的域,g∩是交集函数,|g∩|为交集中匹配成功的个数,那么M、S匹配的表达式为:
true={g∩(M,S)≥t}={|gM(M,S),gS(M,S)|≥t}={|(M∩S,∧)≥t|}
证明 假定方案中所用的不经意传输(Obliviously Transfer, OT)协议是安全的,则真实发送者和模拟发送者的模拟器是存在的,现在利用这两个模拟器作为子程序构建出新的模拟器。
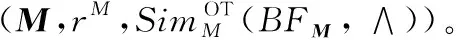
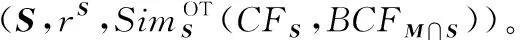
4.2 性能分析
在同态认证过程中,当对多项式验证标签进行运算时,验证标签的大小会被迅速放大,影响认证效率,而这种增加主要来自于同态乘法运算。然而,如果对每一次运算后的验证标签作一次同态解密运算,则可以得到一个类似于新鲜密文大小的新验证标签,从而保证了验证标签的大小维持在一个低水平范围内。本方案中较Catalano等[8]提出的基于算术电路可实用的同态消息认证方案最大的不同在于引进了一个Homomorphic decryption 算法,其作用在于将验证标签的大小降低到类似新鲜密文的大小,从而保证了验证标签大小被保持在一个低水平范围内。Catalano等提出的方案中存在的最大缺陷是多项式验证标签的大小会随电路的深度增加而递增,在他们的方案中通过限制电路深度克服了这一缺陷。然而,他们的解决办法是以牺牲下列条件为代价:事先固定电路所能运算的最大深度值D。在本文方案中不需要事先设定电路的深度值,在每次同态乘运算之后自动调动 Homomorphic decryption算法来降低标签系数,从而可以进行任意次验证计算。本方案中存在的问题是每次调用 Homomorphic decryption算法势必增加方案的复杂度。下面说明方案的复杂度。
验证标签大小的增长主要来源于同态乘法的运算,本文中增强电路的输入可以表示成多项式函数,故电路的深度可以用输入位的对称多项式来衡量本文假设方案中增强电路中输入的验证标签多项式分别表示为y(x1)=a1+a2(x1)2+a3(x1)3和y(x2)=b1+b2(x2)2+b3(x2)3,其中系数(a1,a2,a3)和(b1,b2,b3)分别表示电路输入,那么如何确定这两个多项式相乘结果的次数呢?运用如下结论:
乘两个t位数相当于加t位数,输出位是输入位的一个2次多项式:

t个数相加:3个数相加得到2个数相加,输出位是关于输入位的一个次数最多为2次的多项式:
那么t个数运用这个性质经过log3/2t次相加后得到两个数,输出位的次数为2log3/2t=tlog3/22=t1.71。
两个t位数相加:
进位:

可以类推出:输出位的次数最多为t。
综上所述:乘两个t位数的次数最多为2t1.71t=2t2.71。
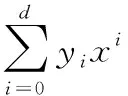
Catalano等[13]运用分级编码的思想,构造了一个基于算术电路扩展的同态认证方案,下面将分别在是否支持密文的复合度、验证标签大小、电路深度大小以及是否支持无上界的验证询问方面与文献[6,8,13]进行比较。具体的比较结果如表1所示。
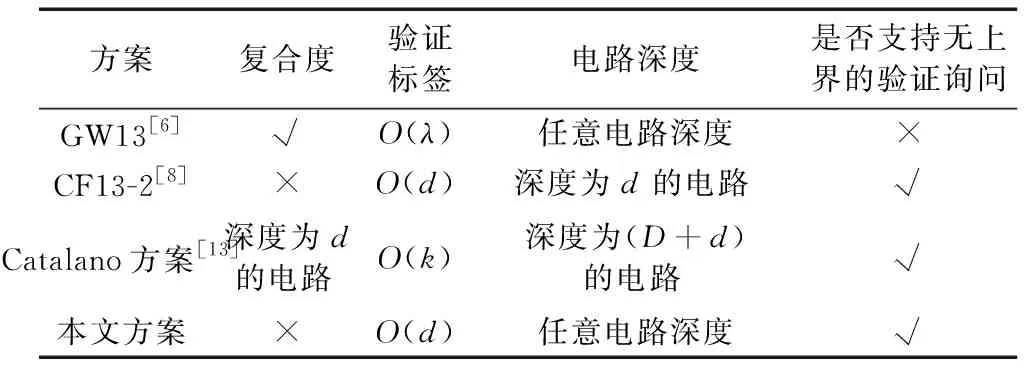
表1 关键词索引结构
通过表1可以得出,本方案相比文献[6,8,13],克服了它们部分缺点,例如相比GW13方案,本方案可以支持无上界的验证询问。不足之处是复合度有所减弱。相比CF13-2方案,本方案在电路深度进行优化,可以进行深度为任意值的电路,在很大程度上增强了用户数据验证的实用性和可操作性。
5 结语
本文将同态解密方法运用到同态认证方案中,构造了云环境下基于运算电路的同态认证方案。通过引入同态解密方法,方案可以达到对密文作任意功能的运算,进一步提高了云数据认证的效率,增强了用户数据的安全性。由于方案中没有讨论增强验证电路的深度是否在Permitted Function集合中,故无法确定方案为全同态认证。进一步的工作是探索方案是否为全同态认证,从而构造效率更高、更为实用的云环境下全同态数据认证方案。

