正则系统在Lebesgue-p范数意义下的快速迭代学习控制
曹 伟,李艳东,王妍玮
(1.齐齐哈尔大学 计算机与控制工程学院,黑龙江 齐齐哈尔 161006; 2.哈尔滨石油学院 机械工程学院,哈尔滨 150027)
0 引言
迭代学习控制算法与神经网络和自适应控制等其他学习类算法不同,迭代学习控制是针对在有限时间区间上具有重复运行特性的被控系统,利用系统存储的跟踪误差对控制输入进行逐次修正,从而实现完全跟踪期望轨迹的目的。由于不需要精确模型信息便可以设计迭代学习控制器,且结构简单等优点,因此迭代学习控制[1]自提出以来,无论是在理论研究方面还是在实际应用中都取得了大量研究成果[2-3]。
到目前为止,关于迭代学习控制大多数相关文献都是在λ范数度量意义下研究算法的收敛性,并指出在λ足够大时算法的收敛性才能够得到保证[4-5]。由于λ范数是有上确界的负指数函数型范数,因此不能客观量化误差的本质特征。文献[6]研究发现,当λ参数值取得较大时,虽然学习算法在理论上是收敛的,但在系统运行初始阶段误差的上确界值往往会超出实际工程允许的误差范围。为避免λ范数上述缺陷,文献[7]在上确界范数度量意义下对比例微分(Proportional-Derivative, PD)型迭代学习控制算法的收敛性进行了研究,发现学习算法只能在系统运行时间区间的某个子区间内是收敛的。文献[8]为使迭代学习控制算法在上确界范数度量意义下是收敛的,研究了运行时间区间可调整和学习律可子区间化进行修正的算法,但算法结构相当复杂,在实际工程系统中很难得到应用。进一步,由于Lebesgue-p范数同时考虑了函数f在整个时间区间上的上确界值和各个运行时刻函数值的p次方积分,因此Lebesgue-p范数在量化和反应函数f的性态方面显得更为合理。基于此文献[9]利用Lebesgue-p范数讨论了迭代学习控制的跟踪性能,但没有涉及算法的收敛性。文献[10]研究了多状态时滞线性系统迭代学习控制的稳定性,并利用Lebesgue-2 范数来评估学习算法的跟踪性能。文献[11]针对线性时不变系统,在Lebesgue-p范数度量意义下对具有反馈信息的PD型迭代学习控制进行了收敛性分析。文献[12-13]在Lebesgue-p范数意义下分析了分数阶迭代学习控制律的收敛性。文献[14]针对一类线性系统在Lebesgue-p范数意义下,分析了加速修正初态误差的迭代学习控制算法的收敛性。进一步,文献[15]在Lebesgue-p范数意义下,讨论了变增益迭代学习控制算法的收敛性。分析文献[10-15]可以发现,虽然这些研究成果避免了采用λ范数度量跟踪误差的缺陷,但这些研究成果都是针对D=0的完全非正则系统进行收敛性分析的,其结论不适用于D≠0的正则系统。原因就在于,对于完全非正则系统,迭代学习控制律中必须有跟踪误差的导数,即微分(Derivative, D)型或比例积分微分(Proportional-Integration-Derivative, PID)型迭代学习律,而对于正则系统则只能使用跟踪误差来修正控制律,即比例(Proportional, P)型迭代学习律。由于传统P型迭代学习算法只利用以往跟踪误差来修正控制律,因此跟踪速度较低。为提高传统P型迭代学习算法的收敛速度,文献[16]提出了一种迭代学习控制算法,但对其收敛性分析仍然采用了λ范数。
鉴于以上分析,本文针对一类正则系统,为提高传统P型迭代学习算法的收敛速度,同时克服采用λ范数度量跟踪误差的缺陷,提出了一种充分利用系统以往存储的跟踪误差和当前跟踪误差信息以及迭代轴上相邻两次误差的差分信号,对控制输入进行逐次修正的快速迭代学习控制算法,给出了Lebesgue-p范数意义下的收敛条件。
1 问题描述
考虑如下一类具有重复运行特性的正则系统:
(1)
其中:k为迭代次数,t∈[0,T]为系统运行的有限时间,xk(t)∈Rn为系统第k次运行时的状态向量,uk(t)∈Rr和yk(t)∈Rm分别为系统第k次运行时的控制输入向量和输出向量,A、B、C、D为适当维数的矩阵。
假设1 每次迭代时系统初始状态与期望初始状态保持一致,即xk(0)=xd(0),k=0,1,2,…。
假设2 存在唯一的理想输入ud(t)使式(2)成立:
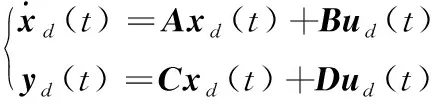
(2)
其中:yd(t)为期望轨迹,xd(t)为期望状态。
1.1 控制目标
本文的控制目标:针对正则系统(1),为克服传统P型迭代学习控制算法收敛速度较低的不足,设计出一种快速迭代迭代学习控制算法,同时利用Lebesgue-p范数对其收敛性进行分析,克服采用λ范数度量跟踪误差的缺陷。
针对这一控制目标,快速迭代学习控制算法设计如下:
uk+1(t)=uk(t)+Lp1ek(t)+Ld1Δek(t)+Lp2ek+1(t)+
Ld2Δek+1(t)
(3)
其中:ek(t)=yd(t)-yk(t)为第k次运行的跟踪误差,ek+1(t)=yd(t)-yk+1(t)为第k+1次运行的跟踪误差。Δek(t)=ek-1(t)-ek(t)和Δek+1(t)=ek(t)-ek+1(t)为迭代轴上相邻两次误差的差分信号,其中Δek(t)称为上一次的差分信号,Δek+1(t)称为当前次的差分信号。Lp1为第k次跟踪误差的学习增益,Lp2为第k+1次跟踪误差的反馈增益,Ld1和Ld2分别为差分信号的学习增益和反馈增益。
由算法(3)可知,当Lp2和Ld2取零时,算法(3)即为开环迭代学习控制算法:
uk+1(t)=uk(t)+Lp1ek(t)+Ld1Δek(t)
(4)
当Ld1、Lp2和Ld2都取零时,算法(3)则变为传统P型迭代学习控制算法:
uk+1(t)=uk(t)+Lp1ek(t)
(5)
现在的问题是针对正则系统(1),采用算法(3)控制,当Ld1、Lp2和Ld2满足什么条件时,系统是收敛的。
1.2 数学基础
为便于分析控制算法的收敛性,给出如下定义和引理:
定义1 向量值函数f:[0,T] →Rn的λ范数定义[1]为:

向量值函数f的上确界范数[10]和Lebesgue-p范数[21]定义为:
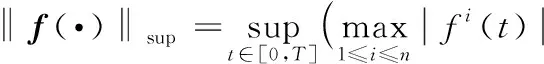
文献[17]中给出了一个重要结论就是:上确界范数是Lebesgue-p范数的特例,即:
引理1[17]如果向量值函数g,h:[0,T] →R是Lebesgue可积的,那么推广的卷积Young不等式为:
‖(g*h)(·)‖r≤‖g(·)‖q‖h(·)‖p

2 收敛性分析
定理1 利用设计的算法(3)控制满足假设条件1~2的系统(1),如果下列条件满足:
1)ρ-1>0;

证明 由系统(1)可知:
ek+1(t)=yd(t)-yk+1(t)=ek(t)-[Cexp(At)xk+1(0)-



(6)
根据假设1,并把式(3)代入式(6)可得:

D(Ld1Δek(t)+Lp2ek+1(t)+Ld2Δek+1(t))=



(7)
整理式(7)可得:

(8)
式(8)两边取Lebesgue-p范数,并应用Young不等式,则得:
‖I+DK2‖‖ek+1(·)‖p≤‖I-DK1‖‖ek(·)‖p+‖Cexp(A·(·))BLd1‖1‖ek-1(·)‖p+‖Cexp(A·(·))BK1‖1‖ek(·)‖p+
‖Cexp(A·(·))BK2‖1‖ek+1(·)‖p+
‖DLd1‖‖ek-1(·)‖p
(9)
整理式(9)得:
(‖I+DK2‖-‖Cexp(A·(·))BK2‖1)‖ek+1(·)‖p≤(‖DLd1‖+‖Cexp(A·(·))BLd1‖1)‖ek-1(·)‖p+(‖I-
DK1‖+‖Cexp(A·(·))BK1‖1)‖ek(·)‖p
(10)
即:
ρ‖ek+1(·)‖p≤ρ1‖ek-1(·)‖p+ρ2‖ek(·)‖p≤
(ρ1+ρ2)max{‖ek-1(·)‖p,‖ek(·)‖p}
(11)
整理式(11)可得:
‖ek+1(·)‖p≤ρ-1(ρ1+ρ2)max{‖ek-1(·)‖p,
‖ek(·)‖p}
(12)
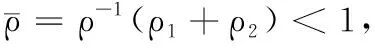
3 仿真实验
为验证本文算法的有效性,考虑如下一类线性正则系统
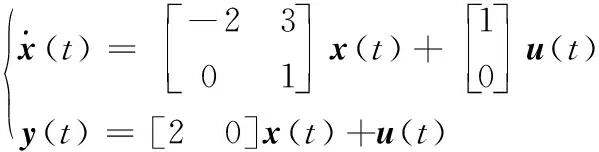
(13)
其中,t∈[0,2]。利用算法(3)控制系统(13),设期望轨迹yd(t)=sin(5t),系统初始状态为x1(0)=0,x2(0)=0,初始控制取u(t)=0,在满足收敛条下分别取LP1=0.3,Ld1=0.1,LP2=0.2,Ld2=0.1。为验证本文提出算法(3)的有效性,分别与开环算法(4)和传统P型算法(5)进行仿真比较,仿真结果如图1~3所示。其中:图1为算法(3)控制时不同迭代次数的输出跟踪曲线;图2为在上确界范数和Lebesgue-2范数意义下跟踪误差曲线;图3为在Lebesgue-2范数意义下算法(3)和算法(4)及算法(5)的跟踪误差曲线。
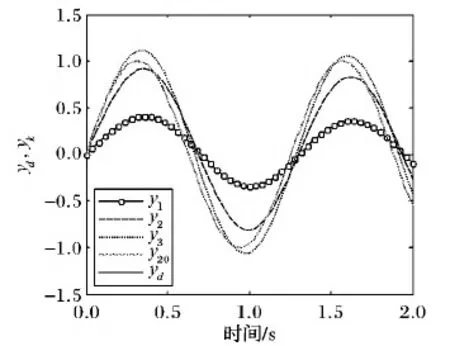
图1 期望轨迹为正弦时算法(3)的跟踪效果
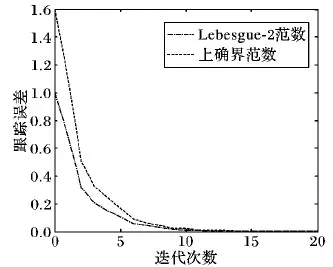
图2 控制算法(3)的跟踪误差曲线
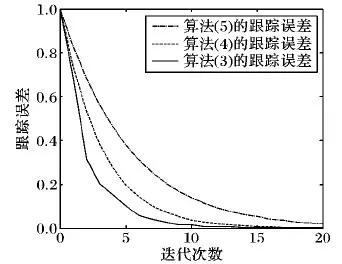
图3 控制算法(3)、(4)和(5)的跟踪误差曲线
从图1可以看出,在第20次迭代后,系统输出在有限时间内已经完全跟踪上了期望轨迹。由图2可看出算法(3)的Lebesgue-2范数和上确界范数都收敛于0。而从图3可看出,算法(3)的收敛速度最高,算法(4)次之,算法(5)的收敛速度最低。其原因就在于,算法(4)是在算法(5)的基础上增加了相邻两次迭代时误差的差分信号;算法(3)则是当前误差和以前误差构成差分信号,而算法(4)只是利用以前误差构成差分信号,算法(3)相比算法(4)充分利用了当前误差信息。为更好说明本文设计的算法(3)的有效性,下面给出算法(3)、算法(4)和算法(5)在不同迭代次数下跟踪误差的数值,如表1所示。
由表1可以看出,算法(3)、算法(4)和算法(5)在第1次迭代时跟踪误差都是0.999 6,经过20次迭代后,算法(5)的误差为0.029 9,算法(4)的误差为0.002 0,算法(3)的误差为0.001 8。从表1的列向数据来看,随迭代次数增加这3种算法的跟踪误差也都能逐次减小,但从表1的横向数据来看,在相同迭代次数下,算法(3)的跟踪误差最小,其次是算法(4),算法(5)的跟踪误差最大。因此,由表1可看出本文设计的快速迭代学习控制算法(3)的收敛速度明显高于算法(4)和算法(5)的收敛速度。
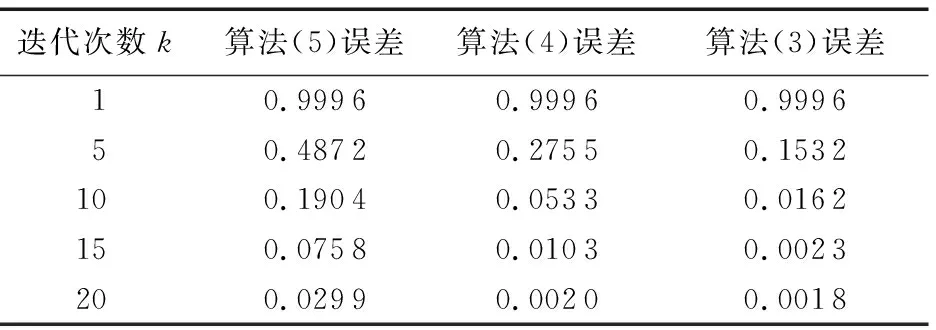
表1 算法(3)、(4)和(5)在不同迭代次数下的跟踪误差
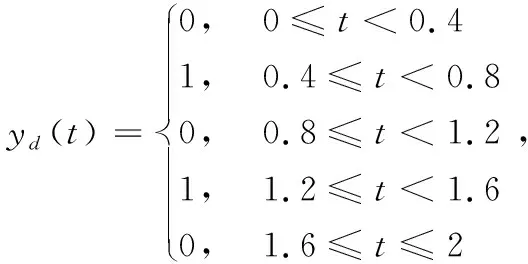
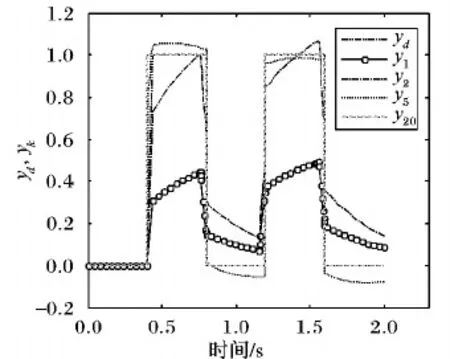
图4 期望轨迹为方波时算法(3)的跟踪效果
由图1和图4可以看出对于缓变和突变的期望轨迹,本文设计的控制算法(3),随迭代次数的增加都能在有限时间区间内实现对不同期望轨迹的完全跟踪。
4 结语
本文针对一类具有输入输出直接传输项的线性正则系统,提出了一种快速迭代学习控制算法,并在Lebesgue-p范数意义下证明了算法的收敛性,给出了使算法收敛的范数形式的充分条件。该算法不仅取得了比传统P型算法较高的收敛速度,而且还避免了采用λ范数度量跟踪误差的缺陷,增大了学习增益选取的自由度。本文也存在一定的不足之处,由于受引理1的卷积限制,本文算法只适用于线性正则系统。因此,在以后研究工作中,可进一步分析非线性正则系统在Lebesgue-p范数意义下的收敛性。
[14] 兰天一, 林辉. Lebesgue-p范数意义下对初态误差进行加速修正的迭代学习控制[J]. 控制与决策, 2016, 31(3): 429-434.(LAN T Y, LIN H. Accelerated modify approach for initial state error iterative learning control in sense of Lebesgue-pnorm [J]. Control and Decision, 2016, 31(3): 429-434.)
[15] 兰天一, 林辉. Lebesgue-p范数意义下区间可调节的变增益加速迭代学习控制[J]. 控制与决策, 2017, 32(11): 2071-2075.(LAN T Y, LIN H. Accelerated iterative learning control algorithm with variable gain and adjustment of interval in sense of Lebesgue-pnorm [J]. Control and Decision, 2017, 32(11): 2071-2075.)
[16] 王洪斌,王艳.机械臂带角度修正的开闭环迭代学习轨迹跟踪控制[J].自动化学报,2010,36(12):1758-1765.(WANG H B, WANG Y. Open-closed loop ILC corrected with angle relationship of output vectors for tracking control of manipulator [J]. Acta Automatica Sinica, 2010, 36(12): 1758-1765.)
[17] PINSKY M A. Introduction to Fourier Analysis and Wavelets [M]. Pacific Grove: Brooks/Cole, 2002: 169-175.

