基于模糊推理的悬臂式隧道掘进机工作性能预测方法

曹文贵，李树林，张永杰

(1.湖南大学岩土工程研究所，湖南 长沙 410082； 2.长沙理工大学土木与建筑学院，湖南 长沙 410114)

基于悬臂式隧道掘进机的隧道铣挖施工方法是一种重要的隧道施工方法[1]，其适应性受悬臂式隧道掘进机工作性能制约，而悬臂式隧道掘进机工作性能是采用悬臂式隧道掘进机进行隧道铣挖施工的适应性及其设备选型的重要依据，因此，合理预测悬臂式隧道掘进机工作性能具有重要的理论与工程意义。可是，悬臂式隧道掘进机工作性能一般采用悬臂式隧道掘进机进行隧道铣挖的瞬时切割速率ICR(instantaneous cutting rate，其定义为悬臂式隧道掘进机在连续铣挖模式下的净掘进速度即单位时间内的切割岩体体积)来综合度量，故合理预测悬臂式隧道掘进机瞬时切割速率ICR是预测悬臂式隧道掘进机工作性能的核心与关键，这正是本文研究的出发点与核心内容。

目前，国内外学者对基于悬臂式隧道掘进机的隧道铣挖瞬时切割速率ICR的预测方法进行了深入而广泛的研究，取得了卓有成效的研究成果[2～7]。已有铣挖瞬时切割速率ICR预测方法主要有经验公式和智能预测模型两类。

前者的研究思路是基于工程实测数据通过拟合分析方法获得ICR的经验关系式，以实现对悬臂式隧道掘进机隧道铣挖瞬时切割速率ICR的预测。例如，Gehring等[2]提出的由岩石单轴抗压强度UCS(uniaxial compressive strength)预测ICR的经验公式；Bilgin等[3]提出的由悬臂式隧道掘进机截割功率P、UCS以及RQD(rock quality designation)预测ICR的经验公式；Rostami等[4]提出的由P、岩石破碎比能耗SE(specific energy)以及能量转移率k预测ICR的经验公式；Copur等[4]提出的由UCS、P以及悬臂式隧道掘进机机重W预测ICR的经验公式；Thuro等[4]提出的由UCS预测ICR的经验公式；Tumac等[5]提出的由UCS或肖氏硬度SH(shore hardness)预测ICR的经验公式； Ocak等[4]提出的由UCS预测ICR的经验公式；Ebrahimabadi等[4]提出的由UCS、RQD以及由巴西劈裂试验测得的抗拉强度BTS(brazilian tensile strength)预测ICR的经验公式； Abdolreza等[6]提出的由UCS、RQD、BTS以及隧道轴线与软弱结构面夹角α预测ICR的经验公式；Kahraman等[4]提出的由点荷载强度IS、BTS、岩块的纵波速度VP、孔隙率n及岩石吸水率Aw等预测ICR的一系列经验公式；Zhang等[7]提出了基于Rostami公式[4]的预测ICR的方法；等等，这些研究反映出对ICR有重要影响的因素主要为围岩岩性(如UCS、RQD、BTS、SH等)和施工设备条件(如P等)，为后续研究提供了非常宝贵的经验与数据，但由于悬臂式隧道掘进机与岩土体相互作用的复杂性，致使不仅目前无法从理论上全面揭示ICR与各岩土参数之间的关系，而且现有经验公式的准确性也难以得到保证，因此，ICR的智能预测方法便应运而生。

悬臂式隧道掘进机铣挖瞬时切割速率智能预测模型的研究思路是利用工程实测数据采用智能分析方法[8](包括神经网络、遗传算法、模糊逻辑等)建立ICR预测模型，以实现对悬臂式隧道掘进机隧道铣挖瞬时切割速率ICR的预测。目前，该类预测方法的研究相对较少， Avunduk等[9]选取UCS和RQD为预测指标提出了基于人工神经网络的ICR预测模型； Ebrahimabadi等[10]以UCS、BTS以及RQD为预测指标提出了基于人工神经网络的ICR预测模型，这些模型为ICR预测方法的研究提供了新思路，并且也取得了一定成效，但是也存在明显的缺陷，其主要表现为它们都只考虑了围岩岩性方面因素而未考虑施工设备条件对ICR的影响，而施工设备条件尤其是机械截割功率P对ICR的影响是不可忽略的，这一点在大量前人研究[3～4]中可以得到很好地证实，因此，有必要建立综合考虑围岩岩性与施工设备条件影响的ICR预测模型，这正是本文研究的核心内容。

为此，本文将在已有研究基础上，充分考虑影响因素的模糊不确定性，并且广泛参考已有工程经验，引入模糊推理方法[11]，深入探讨考虑上述两方面综合影响的铣挖瞬时切割速率ICR预测方法，以期完善悬臂式隧道掘进机隧道铣挖瞬时切割速率ICR预测的理论与方法，为悬臂式隧道掘进机隧道铣挖施工方法的适应性及其设备选型提供依据。

1 基于模糊推理的ICR预测模型

本文建立铣挖瞬时切割速率ICR预测模型从预测指标的选取入手，由前述分析可知，预测指标应从围岩岩性与施工设备条件两方面综合选取，为使所建立预测模型具有较好的可操作性，本文选取这些因素中最为典型且容易获取的指标作为预测指标，它们分别是围岩岩性中表征岩石坚硬程度的UCS[13]和表征岩体完整性的RQD[14]以及施工设备条件中表征悬臂式隧道掘进机等级的机械截割功率P[15]。考虑到它们均具有模糊不确定性，因此，引入模糊推理系统[12]可建立出如图1所示的ICR预测模型。该模型包含三个输入参数(UCS、RQD和P)和一个输出参数(ICR)。下面将分别介绍模型中四个关键步骤即模糊化、模糊规则库、模糊推理机以及去模糊化的处理方法。

图1 基于模糊推理的ICR预测模型Fig.1 Prediction model of ICR based on fuzzy inference

1.1 模糊化

由于模糊推理算法的运算建立于模糊集之上，因此，首先需要将参数经过模糊化处理转化为模糊集，以便后续运算与分析。由前面的分析，岩石坚硬程度、岩体完整性以及悬臂式隧道掘进机等级的取值均具有模糊性与不确定性，例如，根据《工程岩体分级标准》[13]可将岩石坚硬程度按UCS划分为“极软”、“软”、“较软”、“较坚硬”和“坚硬”五级，而实际上在相邻等级区间分界处岩石坚硬程度存在着较大的不确定性与模糊性，因此，引入模糊数学理论[12]，将岩石坚硬程度记为xUCS，故变量xUCS的取值为自然语言中的一些词语如“极软”和“软”等，在模糊数学理论中称类似于xUCS的这类变量为语言变量，而“极软”和“软”等为模糊集。所谓模糊化[12]即通过构造隶属函数等方法将参数的确定值转化为语言变量值的过程。考虑到线性隶属函数的普遍适用性，参考《工程岩体分级标准》[13]可获得xUCS的隶属函数，如图2a所示；同样的，分别依据水利部能源部昆明勘测设计院提出的RQD与岩体完整性关系[14]、Tatiya提出的悬臂式隧道掘进机分级[15]以及Bilgin等[3]、Rostami等[4]、Copur等[4]、Ebrahimabadi等[4]的研究成果可以建立出岩体完整性xRQD、悬臂式隧道掘进机等级xP和掘进速度yICR的隶属函数，如图2b，c,d所示。

图2 语言变量的隶属函数Fig.2 Membership function of linguistic variables

1.2 模糊规则库

模糊规则库是模糊系统的核心，它由一系列的if-then规则[12]组成，可以表示为：

(1)

式中：i——规则编号；

M——规则条数；

于是，通过搜集Hereke隧道[1]、Küçüksu隧道[5]、Istanbul地铁[16]、Çaylrhan煤矿[17]以及Eyüp隧道[18]等共53组实测数据可得到35条模糊规则(相同的模糊规则只保留1条)，如表1所示。值得注意的是，由模糊规则库的形成方法可知，若能通过更多量且围岩岩性与施工设备条件更具多样性的工程实测数据来进一步扩充模糊规则库，则能进一步提高预测的准确性。

表1 模糊规则库Table 1 Fuzzy rule base

注：表中，AUCS一列JR、R、JIR、JJY和JY分别表示极软、软、较软、较坚硬和坚硬；ARQD一列PS、WZXC、JWZ和WZ分别表示破碎、完整性差、较完整和完整；ARQD一列L、M、H和SH分别表示轻型、中型、重型和超重型；BICR一列M、JM、YB、JK和K分别表示慢、较慢、一般、较快和快。

1.3 模糊推理机

前述已得到参数的模糊化方法以及模糊规则库形成方法，还需利用模糊推理机进行运算才能得到推理结果，本文选较常用的Mamdani模糊推理算法[11～12]，它将经典的Max与Min算子[12]作为模糊关系与推理结果合成的运算法则，具体可分为单规则推理与推理结果合成两步，分别如下。

1.3.1单规则推理

1.3.2推理结果合成

上述即为具有2条if-then规则(Ri和Rj)的Mamdani模糊推理算法过程。对于本文模型具有35条if-then规则，其计算过程也一样，首先由每条规则得到单规则推理结果模糊集，然后由Max算子[12]进行合成得到最终推理结果模糊集。

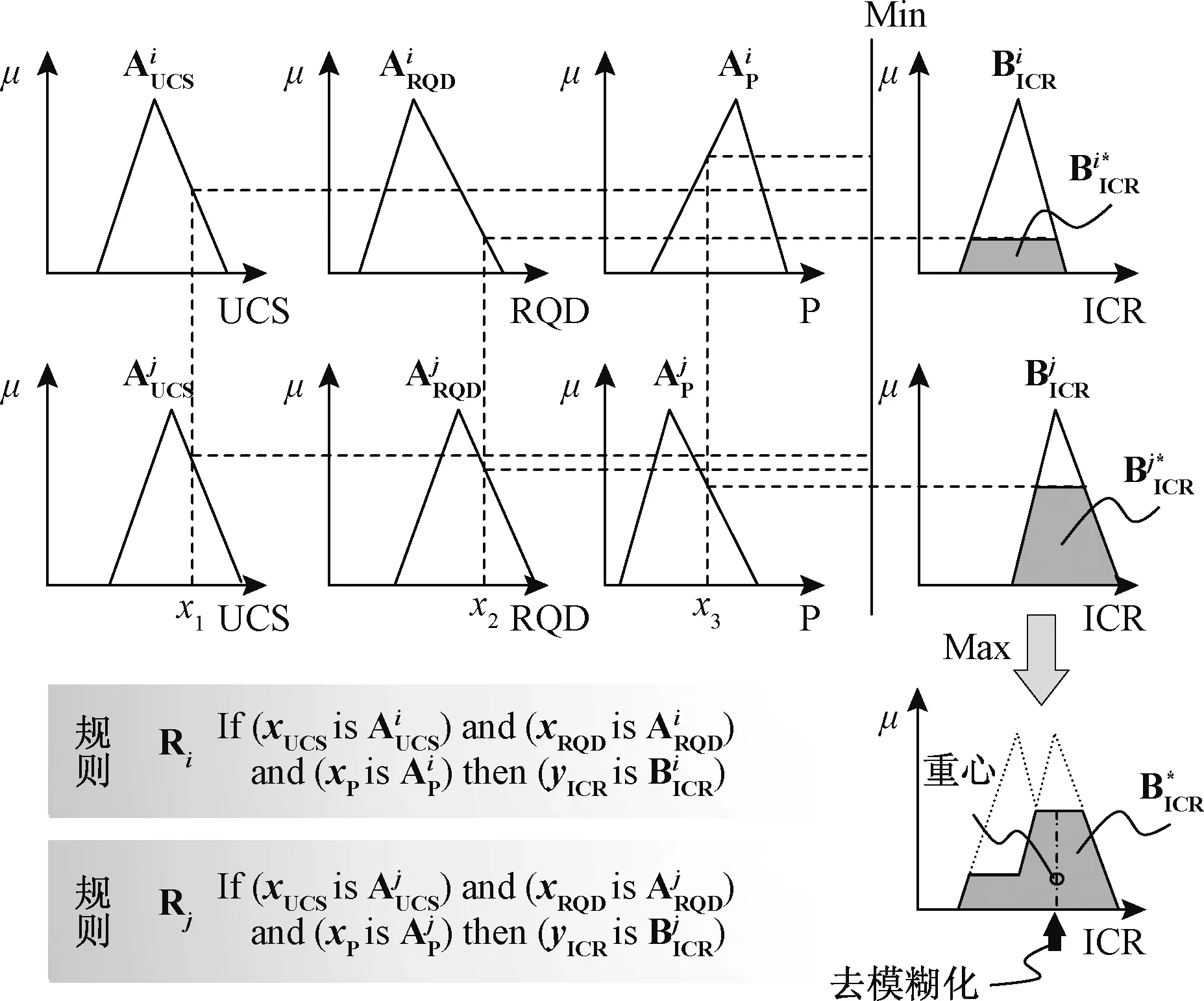
图3 Mamdani模糊推理算法Fig.3 Mamdani fuzzy inference algorithm注：图中纵坐标μ表示隶属度；隶属函数曲线上标注的等表示为该隶属函数曲线对应的模糊集。

1.4 去模糊化

由上述分析可知，经过Mamdani模糊推理算法运算后的结果仍然为一个模糊集，而非确定的值，去模糊化处理就是将这个模糊集转化为确定值即本文模型中ICR预测值。现有去模糊化方法非常多[12]，本文选择较常用且直观合理的重心法[12]对推理结果进行去模糊化处理，如图3所示，其中阴影部分重心可通过定积分进行计算，这里不再列出具体计算公式。

2 工程实例

2.1 工程概况

前述已建立出悬臂式隧道掘进机隧道铣挖瞬时切割速率ICR预测方法，为了验证本文方法的合理性，以Ebrahimabadi等[10]基于DOSCO MD1100型悬臂式隧道掘进机(截割功率82kW)在Tabas煤矿进行现场试验测得的62组实测数据(表2)进行实例分析。

表2 试验数据[10]Table 2 Experimental data

2.2 结果与分析

将实例数据代入本文所建立的基于模糊推理的ICR预测模型进行分析，并将其分析结果与Bilgin公式[3]、Thuro公式[4]、Tumac公式[5]、Ebrahimabadi公式[10]和人工神经网络[10]方法的预测结果进行对比分析，如图4所示。由图4可知，前15组实例中，本文方法预测值与实测值最为接近，其次为Bilgin公式[3]预测值。第16～35组实例中Tumac公式[5]预测值与实测ICR最为接近，其次为本文方法预测值。第36～62组实例中本文方法预测值与实测ICR最为接近，其次为Thuro公式[4]预测值。就综合预测效果而言，本文方法具有较明显的合理性。

图4 本文与已有模型和实测结果对比Fig.4 Comparison of the predicted values achieved from the new model and previous model with the measured data

3 结论

本文综合考虑围岩岩性及施工设备条件对悬臂式隧道掘进机铣挖瞬时切割速率的影响，并结合各影响因素的模糊不确定性特点，对铣挖隧道的悬臂式隧道掘进机工作性能预测方法进行了深入研究。由此可得如下结论：

(1)考虑围岩岩性与施工设备条件因素的综合影响及其影响的模糊不确定性，引入模糊推理理论，提出了基于模糊推理的隧道铣挖瞬时切割速率ICR的预测方法。

(2)本文方法不仅能反映围岩岩性与施工设备条件的综合影响及其影响的模糊性与不确定性特点，还因本文方法最大限度地利用了已有工程实测数据或工程经验而使本文方法的实用性得到了强有力的保证。

(3)通过与现有方法分析以及实测结果的比较分析，表明了本文方法的合理性与可行性。