波状水平段管柱屈曲特性试验研究
王昊,张辉 史玉才
(中国石油大学(北京)石油工程学院,北京 102249) (中国石油大学(华东)石油工程学院,山东 青岛 266580)
对于大位移井和长水平段水平井来说,钻柱屈曲(特别是螺旋屈曲)会显著增加钻柱与井壁的摩擦阻力,影响钻柱下入和钻压传递,严重时甚至会导致钻柱“自锁”。目前,国内外众多学者已开展过钻井管柱屈曲特性理论和试验研究,推导了垂直井、斜井、水平井和弯曲井等不同井眼形状下的管柱临界屈曲载荷和附加摩擦阻力计算公式[1~10],并探讨了钻杆自重、扭矩和摩擦系数等因素对管柱屈曲的影响[11~19]。而实钻井眼轨迹往往同时存在井斜角和方位角变化,水平段轨迹近似呈波状变化,使钻柱屈曲现象更加复杂。通过改造现有水平井管柱屈曲特性试验装置开展试验,笔者探讨了波状水平井眼中钻柱的螺旋屈曲临界载荷和屈曲后摩擦阻力随井眼曲率和环空间隙的变化规律,为钻井现场合理选择钻柱尺寸以及避免钻柱屈曲提供了依据。
1 试验装置

图1 水平井管柱屈曲特性试验装置示意图
模拟试验装置见图1。主体部分为水平放置的钢架结构,可模拟有效井眼长度约9.6m,在比例系数1∶10的理想情况下可模拟钻井现场96m的实际水平井段。其中,模拟井眼采用特制的厚壁有机玻璃管(约1m/根,依靠夹持装置连接并保持同心),模拟钻柱采用特制的ABS工程塑料管(密度1.1g/cm3,弹性模量2.3GPa,约0.3~0.9m/根,依靠螺纹连接),试验装置两端安装压力传感器,用以测量试验中加载端和接受端的受力情况。
2 试验方案
试验方案设计依据相似方法建立。现场井眼曲率1°/30m经计算可化为室内曲率约0.3°/m。钻柱所受轴向压力遵从相似准则[20],即为:
(1)
式中:cd为模拟钻柱与现场钻柱的轴向压力之比,1;cE为模拟钻柱与现场钻柱的弹性模量之比,1;cl为试验与现场的几何尺寸之比,1。
ABS工程塑料管的弹性模量为2.3GPa,现场钢制钻柱的弹性模量为210GPa,可导出模拟钻柱与现场钻柱的轴向压力相似关系约为1∶9130。基于上述相似准则及材料的物理性质可知,实验室内轴向压力1N约等于现场实际轴向压力9kN。
根据计算结果,采用弦长代替弧长,斜直段代替弯曲段的方法设计波状井眼,此方法误差较小,易于实现。波状水平段设计参数见表1,模拟示意图如图2所示。

表1 波状水平段设计参数

图2 波状水平段(井斜角)模拟图
3 试验结果分析
3.1 完全水平井眼管柱屈曲分析
3.1.1完全水平井眼临界屈曲载荷分析
螺旋屈曲临界载荷由试验数据分析并结合试验现象共同确定。通常情况下,在接收载荷—加载载荷曲线中,临界载荷点处出现“N”型波折点且曲线斜率发生改变;在摩擦阻力—加载载荷曲线中,临界载荷点为加载过程中曲线斜率显著变化点。
试验得到的螺旋屈曲临界载荷汇总结果见表2。可以看出,临界屈曲载荷与钻柱刚度和井眼间隙密切相关。在同一种井眼内径下,采用较大尺寸的钻柱会增加钻柱刚度并减小井眼间隙,最终可提高临界屈曲载荷;反之,采用较小尺寸的钻柱会降低钻柱刚度并增大井眼间隙,最终会降低临界屈曲载荷。在同一种钻柱外径下,井眼内径的增大也将导致临界屈曲载荷降低。
对试验得到的螺旋屈曲临界载荷进行公式拟合,见式(2)。将式(2)与现有的钻柱螺旋屈曲临界载荷的典型理论公式相比较,发现试验值介于Chen[3]公式(3)和Wu[21]公式(4)之间:

表2 水平井眼中钻柱螺旋屈曲临界载荷试验数据表组别模拟井眼内径
(2)
(3)
(4)
式中:Fhel为试验螺旋屈曲临界载荷,N;F1、F2分别为Chen和Wu公式理论螺旋屈曲临界载荷,N;r为钻柱与井眼的径向间隙,m;θ为井斜角,rad;EI为钻柱抗弯刚度,N·m2;w为钻柱线重,N/m。
由于式(2)与式(3)较为接近。因此,选取Chen公式作为理论螺旋屈曲临界载荷的参考公式。
3.1.2完全水平井眼摩擦阻力分析
对于钻柱屈曲后摩擦阻力方面的研究,目前国内外学者大多使用管柱与井壁的接触力公式进行分析[22]。在摩擦系数因试验设备条件而为定值的情况下,管柱摩擦阻力的大小由接触力直接决定。试验中直接采用接触力大小来探讨摩擦阻力的变化规律。接触力计算公式如下:
(5)
式中:W为接触力,N;r为钻柱与井眼的径向间隙,m;F为管柱实际轴向载荷,N;L为钻柱长度,m。

图3 完全水平井眼摩擦阻力-加载载荷变化曲线
试验中,摩擦阻力取加载载荷和接收载荷之差。典型的摩擦阻力-加载载荷曲线见图3。可以看出,钻柱屈曲后的摩擦阻力也与钻柱刚度和井眼间隙密切相关。因此,在同一种井眼内径下,采用较大尺寸的钻柱可提高临界屈曲载荷并降低摩擦阻力,采用较小尺寸的钻柱会降低临界屈曲载荷并增加摩擦阻力,而在采用同一种钻柱时,井眼内径的增大也会降低临界屈曲载荷并增加摩擦阻力。
此外,按接触力公式(5)计算各钻柱组合的接触力大小,计算结果同表2。结合图3可以看出,试验得出的摩擦阻力排序与计算给出的接触力排序相符,且摩擦阻力曲线在螺旋屈曲点后近似为二次函数。试验结果表明,现有理论给出的接触力计算公式能较好地反映实际情况。
3.2 波状水平井眼管柱屈曲分析
3.2.1波状水平井眼临界屈曲载荷分析

表3 波状水平井眼中钻柱螺旋屈曲临界载荷试验数据表
与水平井眼确定螺旋屈曲临界载荷的方法相同。试验共有2种井筒、2种钻柱、3种波状井眼曲率,在不同管柱组合及波状井眼曲率条件下,各组试验都可根据曲线得到试验螺旋屈曲临界载荷(模拟井眼及钻柱组合关系同表2),汇总结果见表3。
根据表3的结果,对不同波状井眼曲率条件下试验所得的临界载荷值进行拟合,拟合结果见式(6)~(8)。与完全水平井眼钻柱屈曲试验结果对比分析不难发现,同一种管柱组合随波状井眼曲率的增大,螺旋屈曲临界载荷大多略有下降,部分保持不变。说明随着波状水平段井眼曲率的增大,钻柱的临界屈曲载荷呈现减小趋势,钻柱更易形成屈曲,易对钻井作业带来困难。因此,在钻井现场时应当尽量保持井眼轨迹与设计轨迹一致,避免出现较长波状段影响作业效率。
井眼曲率为0.5°/m时:F0.5=2.5986(EI·w/r)1/2
(6)
井眼曲率为0.8°/m时:F0.8=2.4593(EI·w/r)1/2
(7)
井眼曲率为1.3°/m时:F1.3=2.2841(EI·w/r)1/2
(8)
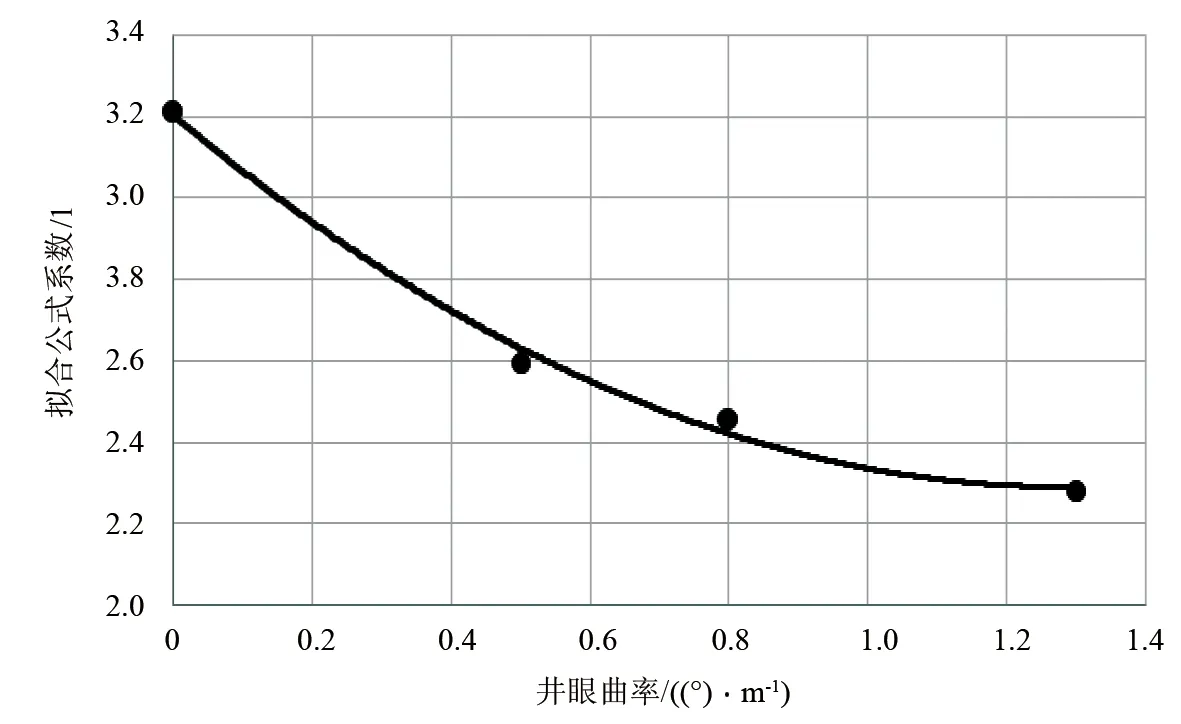
图4 拟合公式的系数随波状水平段曲率变化曲线
为进一步探讨波状水平段井眼曲率对螺旋屈曲临界载荷的影响,对拟合公式(6)~(8)中的系数进行回归分析拟合,如图4所示。回归分析结果表明,该系数随波状水平段井眼曲率变化约呈二次函数关系,即为螺旋屈曲临界载荷随波状井眼曲率增大约呈二次函数关系变化。
3.2.2波状水平井眼摩擦阻力分析
不同波状井眼曲率条件下典型的摩擦阻力-加载载荷曲线如图5所示。图5(a)与图5(b)为外径15.30mm的模拟钻柱,内径分别为24.30mm和31.80mm的模拟井眼,在不同井眼间隙条件下的摩擦阻力-加载载荷曲线。当水平段从完全水平到波状曲率为1.3°/m,井眼曲率对摩擦阻力影响规律是不同的。在图5(a)中(24.30mm井眼+15.30mm钻柱),摩擦阻力随波状井眼曲率的增加而增加;在图5(b)中(31.80mm井眼+15.30mm钻柱),摩擦阻力随波状井眼曲率的增加呈减小趋势,并且各条曲线分离程度较低,曲线之间距离较近。
图5(c)与图5(d)为外径18.00mm的模拟钻柱,内径分别为24.30mm和31.80mm模拟井眼,摩擦阻力随波状井眼曲率变化规律。可以看出,图5(c)与图5(d)中摩擦阻力随波状井眼曲率变化规律均与图5(a)相同,随波状井眼曲率增加而增加。
结合完全水平井眼和波状井眼中临界屈曲载荷变化规律分析结果,认为出现上述差异的关键原因是井眼间隙所致。当井眼间隙相对较小时,随井眼波状段曲率的增加,螺旋屈曲临界载荷降低,从而管柱更易发生屈曲,因此在同样加载载荷下,较大曲率井眼中的钻柱屈曲程度更严重,摩擦阻力也就越大。当井眼间隙相对较大时,钻柱受井眼内壁约束减小,从而出现不同的试验现象。

图5 不同尺寸井眼、钻柱组合情况下各井眼曲率对应的波状水平井眼摩擦阻力与加载载荷关系曲线

图6 波状井眼曲率为0.5°/m时,不同管柱组合的摩擦阻力与加载载荷关系曲线
此外,还对比分析了同一种波状井眼曲率条件下,不同管柱组合的摩擦阻力变化规律。以波状井眼曲率0.5°/m为例,典型的摩擦阻力-加载载荷曲线如图6所示。可以看出,摩擦阻力按组别由小到大排列顺序仍然与计算的接触力公式系数排序相同,再次证明接触力理论公式适用性较强,且波状井眼中管柱屈曲随管柱尺寸的变化规律与完全水平井眼相同。
4 结论与建议
1)在波状水平井眼中钻柱更易形成屈曲,钻柱在螺旋屈曲后的摩擦阻力随加载载荷变化近似呈现二次函数关系,与完全水平井眼中接触力理论公式特征相似。
2)在试验所选0~1.3°/m的室内波状井眼曲率范围内,管柱的螺旋屈曲临界载荷随波状井眼曲率的增大而减小,摩擦阻力基本上随波状井眼曲率的增大而增大,但是当井眼间隙较大时则有可能出现不同。
3)现场钻井应尽量减少扭方位和增斜降斜的频率,以免形成波状屈曲井眼,影响钻进效率。
4)建议后续试验中将波状段设计为关于中心轴线对称分布,且两边波数相等以便减小试验误差;建议密封井筒并灌钻井液(或清水),以探究钻井液对钻柱屈曲特性的影响。

