运筹学在工程管理中的应用

2018-10-15 01:20王雅婧上海城建职业学院上海200438

建设监理 2018年6期

王雅婧（上海城建职业学院，上海 200438）

运筹学是一门在 20 世纪 40 年代初期诞生的新兴学科。它主要解决了如何最合理地分配和利用有限的物资，使之效益最大化的问题。从运用的角度去看，运筹学涉及的领域较广，主要有工业生产、农业生产、物料运输、人员分配、资源利用、设备更新、工序流程等。它与同时代兴起的系统工程、技术经济学、生产组织与计划学等学科相互渗透、相互作用，共同奠定了现代工程管理的理论基础。工程管理是将工程技术与管理学相互结合，使用科学的管理手段和决策方法以及合理的已有施工技术，实现项目全过程周期内的综合集成和多目标优化。由此可以看出，运筹学在工程管理中有着巨大的作用。本文将从钢筋下料问题、工料运输线路问题、运输机具配置问题、机具更新问题等几个方面，讨论运筹学在建筑工程管理中的实际应用。

1 钢筋下料问题

工程管理的一个首要的任务就是要研究项目的经济可行性。除了做好前期的可行性研究之外，在施工过程中的用料准备也是一个关键因素。使用运筹学中的线性规划模型可以解决材料的最优使用问题。以下就如今建筑工程项目中用量较大，材料费用较高的钢筋为例展开讨论。

以一根钢筋混凝土梁为例，假设该梁长伸入墙体，总长度为 6 240 mm，砖墙厚度为 240 mm，梁截面为 200 mm×500 mm。该梁内部埋设 5 根钢筋。在此处以 3 条钢筋为例：1 号钢筋为 2 根 φ25 的钢筋，保护层厚度为 25 mm，配置在梁底部，在梁端向上垂直弯起 200 mm，端部有半圆形弯钩，每个弯钩增加长度为 4 D；2 号钢筋为 2 根 φ12的钢筋，保护层厚度为 25 mm，设立在梁的上部，端部有半圆形弯钩，每个弯钩增加长度为 4 D；5 号钢筋为 φ6 的箍筋，沿梁全长排列，中间间距为 200 mm，保护层厚度为 25 mm。如果需要建造这一规格的钢筋混凝土梁 100根，需要使用多少根 20 m 的钢筋最为合理？

首先，计算该梁的钢筋下料长度。本文以这 3 组钢筋为例，分别计算其下料长度：

1 号钢筋下料长度 L=(6 240+2×200－2×25) －2×2×25+2×6.25×25=6 802 mm；2 号钢筋下料长度L= 6240－2×25+2×6.25×12=6 340 mm； 5 号箍筋宽度 B=200－2×25+2×6=162(mm) ，高度 H=500－2×25+2×6=462 mm，下料长度 L=(162+462)×2+50=1 298 mm。

从计算结果来看，需要切割 3 种长度的钢筋，分别为6.802 m、6.34 m 和 1.298 m。为了施工实际的操作方便，我们可以将长度进行四舍五入后得出，剪裁长度为 1 号钢筋长度 6.8 m、2 号钢筋长度 6.4 m、5 号箍筋长度 1.3 m。假设购入的成品钢筋长度为每根 20 m，根据一般经验，下料之前可以给出如下 5 个方案。方案 1：1 根 20 m 的钢筋可以剪裁 1 号钢筋 2 根、2 号钢筋 1 根，合计长度为20 m；剩余料长为 0。方案 2：1 根 20 m 的钢筋可以剪裁1 号钢筋 1 根、2 号钢筋 2 根，合计长度为 19.6 m；剩余料长 0.4 m。方案 3：1 根 20 m 的钢筋可以剪裁 2 号钢筋2 根、5 号箍筋 5 根，合计长度为 19.3 m；剩余料长 0.7 m。方案 4：1 根 20 m 的钢筋可以剪裁 2 号钢筋 3 根，合计长度为 19.2 m；剩余料长 0.8 m。方案 5：1 根 20 m 的钢筋可以剪裁 1 号钢筋 2 根、5 号箍筋 4 根，合计长度为18.8 m；剩余料长 1.2 m。

由此，根据这五种钢筋剪裁方案，假设 Xi为 i 种方案下料的根数(i=1，2，3，4，5)。限制条件为，使剪裁后的剩余钢筋长度为最短，且最后 100 根梁里每根梁都分别有1 根 1 号钢筋、1 根 2 号钢筋和 1 根 5 号箍筋。

由此，可以建立线性规划模型如下：

为了方便计算可以将该式通过对偶性质转化成标准形式，由于线性规划模型可以有无数解，这里选用其最优解，四舍五入后，得到答案 x1=47，x2=0，x3=17，x4=0，x5=3，将最优解相加，得到合计根数为 67 根。因此，需要67 根 20 m 的钢筋就可以完成 100 根该梁的 1 号钢筋、2 号钢筋、5 号箍筋的下料准备。

2 工料运输线路问题

在建筑工程项目中经常需要运输各种工料，在每次运输过程中都会产生机械使用费和其他的费用。如果能通过计算来确定最短路线，则可以减少由于线路问题产生的额外费用，在一定程度上减少资源的浪费。假设由于地质条件关系，需要换填一部分土方，从 A 地到 E 地，再由 E 地去往 A 地，如图 1 所示。

图 1 运输最短线路示意图

要得出图 1 较为直观的最短路线，为了减少错误，本文通过排列邻接矩阵来计算最短路线问题[1]。首先，根据图示列出该有向图的邻接矩阵 A；然后，将两个邻接矩阵 A 自定义相加，得到第二级邻接矩阵 B1；将 B1与 A 自定义相加得到第三级邻接矩阵 B2；重复之前一步，得到第四级邻接矩阵 B3及第五级邻接矩阵 B4；验证第四级邻接矩阵 B3和第五级邻接矩阵 B4相等。至此，矩阵计算结束。

由此可以看出，从 A 地去往E地的最短路径为 9，经由A、D、E。另外，从 E 地去往 A 地的最短路径为 6，经由E、D、C、A。应用这种方法，可以准确推断出最短路径。

由此可以看出，从 A 地去往 E 地的最短路径为 9，经由 A、D、E。另外，从 E 地去往 A 地的最短路径为 6，经由 E、D、C、A。应用这种方法，可以准确推断出最短路径。

3 运输机具配置问题

建筑工程中，项目工程造价的直接工程费由人工费、材料费、施工机械使用费所组成。因此，机械的使用方式直接关系到工程造价费用的高低。以材料运输中使用的卡车为例，该卡车载重量为 15 t，用来装载 3 种需要运输的材料，每辆卡车都必须装这 3 种货物。若将卡车的载重量作为一个资源，这类问题在运筹学中称为“背包问题”[2]。现有 A、B、C 3 种货物，设：A 物品重量为 3 t，价格为 1 万元；B物品重量为 4 t，价格为 2 万元；C 物品重量为 5 t，价格为3 万元。如果把每种货物作为一个阶段，那么 n=3，将货物的件数设为 x1、x2、x3；卡车限重为 15 t，因此卡车装载的状态限制条件为 15。就可以列出数学模型：

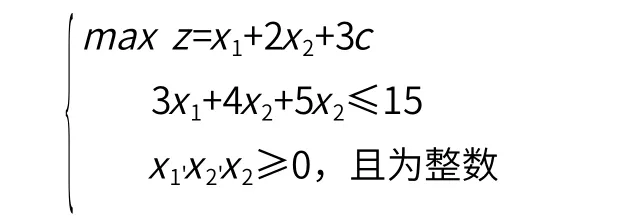
为了方便计算，可以将该式通过对偶性质转化成标准形式，再进行解答，得到这一线性规划模型的最优解为x1=2、x2=1、x3=1。因此，A 物品装载量为 2 个单位，B 物品装载量为 1 个单位，C 物品装载量为 1 个单位。将件数乘以每种货物的单价，汇总就可以得到该货车的最高装载价值为 7 万元。该模型可用于有状态限制条件下装载量的最优问题的解法。

4 机具更新问题

随着现代科学技术的高速发展，在实际项目中，施工机具的更新也成为了一项重要的支出。因此，施工设备的更新也成为工程管理的一项重要内容。在此，本文主要讨论如何确定是否该更新设备以及什么时候该更新设备的问题[3]。

假设有施工企业在 3 a 前购入一价值 50 000 元的专业施工设备。估计这套设备下一年度的使用费为 15 600 元，以后每年增加 4 000 元。现在出了一款新设备，其原始价值为 20 000 元，估计第一年的使用费为 8 000 元，预计以后逐年增加 2 000 元。设新设备使用寿命为 10 a。如果该两款设备都是专为此项目单独设计，这两款设备的残值均为 0，不能出售；若 i=10%，那么是否该更新此设备？

(1) 根据假定条件，计算旧设备的经济寿命。为了计算方便，设定该设备的残值任何时候都为 0，因此可以列出以下的式子：

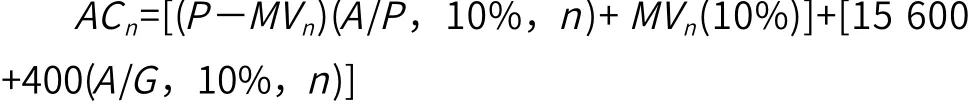
其中：AC 为年度费用，MVn为设备残值，P 为设备现值，A/P 为等额支付资金恢复系数，A/G 为均匀梯度系数，n 为使用年数。

从以上式中，可以看出年度费用等于年度使用费，而且是每年增加的。求出年度费用最低的年份，n=1。此时，第一年的年度使用费为 15 600 元。

(2) 根据假定条件计算新设备的经济寿命，此时，新设备的残值也假定为 0。计算结果如表 1 所示。

从表 1 计算结果可以看出，年度费用在第五年的时候最低，在第六年年度费再度上升。因此，新设备的经济寿命为 5 a，此时的年度费用为 16 896.2 元。

(3) 对比新旧设备的年度费用：

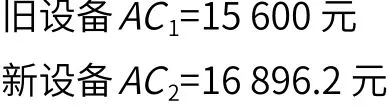
因此，在此条件下，该设备更新费用比使用旧设备的费用高，从经济效益上讲，暂时不应该考虑更新该款设备。如果根据上述方法计算得出的新设备比旧设备的年度费用低的话，则应该考虑更新设备。

假设有一项目研究期为 5 a，需要更新一款设备，该设备的使用寿命也为 5 a，每年都可以更新。使用费用现值为P，i=10%。设 P1=105 万元，P2=142 万元，P3=184 万元，P4=256 万元，P5=310 万元。根据动态规划计算可得设备使用费用终值 F：

从以上计算结果可以看出，该设备在使用 3 a 后更新，加上之后 2 a 的使用费用的总费用为 291 万元，比使用 5 a的使用费现值的 310 万元要小。因此可以分析得出：该方案为最优方案。

5 结语