一种新型电池热管理方案的影响因素研究

江振文，杜鸿达，郑心纬，杜明徽，康飞宇

（清华大学深圳研究生院 能源与环境学部，广东 深圳 518055）

0 引 言

当今社会条件下，随着污染与能源消耗的加剧，人们对节能与环保越来越重视。电动汽车作为一种环保高效无污染的新型汽车，已经受到大众的广泛关注。发展电动汽车，关键是发展动力电池，而锂离子电池由于具有能量密度高、重量轻、体积小、安全等独特优势[1]，成为国内外的研究重点。但是，锂离子电池受温度影响很大，温度过高或过低都不利于锂离子电池性能的发挥[2]。温度过高，锂离子电池容易发热，甚至爆炸；温度过低，电池充放电很浅，不能充分发挥性能。因此，一个适当的电池热管理对动力电池具有极大意义。

目前，传统的电池热管理系统主要包括空冷式散热系统和水冷式散热系统。但是，泵、风扇和必要的组件会使得系统复杂，同时降低电池的能量利用效率[2]。以相变材料为基的热管理方法作为一种新型的热管理方式，主要是利用相变材料（PCM）的融化潜热吸收电池产生的热量而对电池进行冷却散热，同时将电池放出的热量以潜热的形式储存起来。当电池在低温下工作时释放出来，以改善电池的低温性能，且相变材料具有绝缘、无毒、成本低等优点[3]，具有广阔的市场发展前景。然而，电动车行驶过程中，由于电池的持续产热，在某些极端条件下，可能会造成PCM冷却失效的问题，导致电池的温度继续升高，给电动车带来安全隐患。水冷式散热具有冷却速度快、冷却效率高等优点，可将其与以PCM为基础的散热相结合，一方面利用相变材料大潜热吸收电池产生的热量，另一方面利用水冷方式将PCM中存储的能量及时带走，保证对动力电池的持续散热。同时，由于水管只与PCM接触，避免了与电池的直接接触可能带来的隐患，具有更高的安全性。

在PCM已经从电池组中吸热的基础上，本文通过对PCM散热进行仿真，以1 800 s时PCM表面温度为监控参数，探究了影响PCM散热效果的几个主要影响因素，并对其影响力大小进行分析，以期为之后的电池热管理方案设计及参数优化提供帮助。

1 数值模拟

1.1 仿真方案及模型建立

为了简化模型，只画出在PCM中嵌入水管的冷却模型，如图1所示。水管位于PCM中心位置，在水管中加入流动水，通过改变不同参数确定不同影响因素对PCM散热的影响。相变材料的尺寸为100 mm×100 mm×500 mm，水管直径D=20 mm，长度l=500 mm，厚度为1 mm，水管材料为Al，内部通的冷却液体为水。

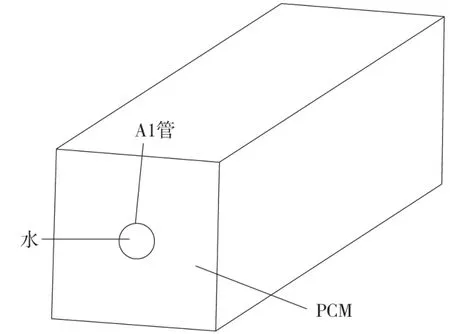
图1 PCM水冷散热模型

1.2 数值模拟及方程

相变过程中，相变材料的焓会急剧增加。为简化问题，方便对PCM进行散热研究，本仿真对相变材料做出如下假设[4]：

（1）石蜡/膨胀石墨复合相变材料内部各物质分布均匀，且物性参数各向同性；石蜡融化后再膨胀，石墨内不会流动；

（2）相变材料的比热容、密度计导热系数、相变潜热，在整个过程始终为恒定值。

基于以上假设，数值模拟中的控制方程为[4]：

仿真过程中，管内流体的能量守恒方程为：

相应的动量守恒方程为：

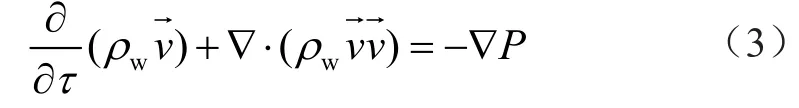
流体连续性方程为：

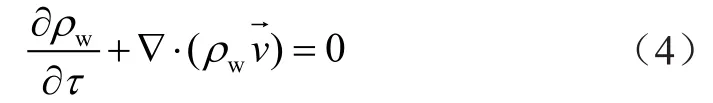
1.3 CFX处理

本次仿真求解器采用CFX。仿真模拟中，PCM初始温度设为50 ℃，冷却液体为水，初始温度为25 ℃，水流速为0.5 m/s。假设整个系统与外界无换热，并忽略整个系统的接触热阻。在CFX前处理中，将动量方程方程设置为湍流，将每次迭代补偿设置为100，以便更快速、精确地求解动量方程。

2 计算结果与分析

2.1 PCM尺寸对PCM表面温度的影响

在水温度为25 ℃、流速为0.5 m/s、水管直径为20 mm条件下，当相变材料侧面长度分别为50 mm、70 mm、80 mm、90 mm、100 mm及120 mm时，相变材料表面温度变化情况及温度分布图如图2、图3所示。

可以看到，随着时间的增加，PCM表面温度逐渐下降，但不同尺寸的PCM温度下降速度不同。随着PCM尺寸的增加，PCM表面温度下降速度明显减小。原因是在热导率、与水管接触面积相同的情况下，热量传递速度相同，PCM的尺寸越大，热量越多，传递的越慢，导致温度降低的速度会明显降低。当PCM的尺寸为100 mm×100 mm×500 mm时，在时间为1 800 s、温度降低到30 ℃时，对于电池来说，也处于正常的工作范围。

图2 不同PCM尺寸下PCM表面温度随时间变化关系图

图3 不同PCM尺寸下PCM表面温度分布图

2.2 水管直径对PCM表面温度的影响

当水管的外径分别为10 mm、15 mm、20 mm、25 mm、30 mm和40 mm时，相变材料表面温度变化情况如图4、图5所示。由图4可以看到，在保持其他参数不变的情况下，随着水管管径的增加，PCM表面温度逐渐下降，且PCM表面温度是随着管径的增加而均匀变化，平均管径每增加1 mm，PCM表面温度降低2 ℃。图5显示了仿真结束时不同管径下的温度分布云图，与上述结果值吻合。

图4 不同管径下PCM表面温度随时间变化关系示意图

图5 不同管径尺寸温度分布图

2.3 PCM导热率对PCM表面温度的影响

当PCM热导率分别为1 W/（m·K）、3 W/（m·K）、5 W/（m·K）、7 W/（m·K）、9.795 W/（m·K）和 15 W/（m·K）时，PCM表面温度随时间变化关系如图6所示。

图6 不同热导率下PCM表面温度随时间变化关系示意图

可以看出，当PCM热导率小于5 W/（m·K）时，随着热导率的增加，PCM表面温度降低明显。例如，当热导率为1 W/（m·K）时，PCM表面温度在1 800 s时为48.4 ℃；当导热率增加到3 W/（m·K）后，PCM表面温度变为43.2 ℃；当导热率大于7 W/（m·K）后，随着导热率的增加，PCM表面温度降低速度明显减小。

关于这种现象产生的原因可以用热阻的概念来解释[3]。热量传热的简化表达式为：

其中，Δt为PCM与冷却水之间的温度差，℃；σ为热量传递距离，m；k为导热系数，W/（m·K）；h为换热系数，W/（m2·K）；q为热流密度，W/m2。

在等式右边其他条件都相同的情况下，随着热导率的增加，PCM与冷却水之间的温度差Δt逐渐减小，所以PCM的温降减小，从图7的分布云图中可以看到这一点。

2.4 水流速对PCM表面温度的影响

保持其他条件不变，设置水流速分别为0.1 m/s、0.3 m/s、0.5 m/s、0.7 m/s、0.9 m/s和 1.2 m/s时，PCM表面温度变化情况如图8、图9所示。可以看到，随着水流速的增加，PCM表面温度总体呈下降趋势。当水流速小于0.5 m/s时，PCM表面温度降低明显；当水流速从0.1 m/s增加到0.3 m/s时，PCM在1 800 s时，表面温度从41.3 ℃降低到36.5 ℃，温度下降接近5 ℃；随着流速的进一步增加，PCM表面温度下降缓慢，如从0.5 m/s增加到2 m/s时，温度只降低了2.1 ℃。

图7 不同热导率温度分布图

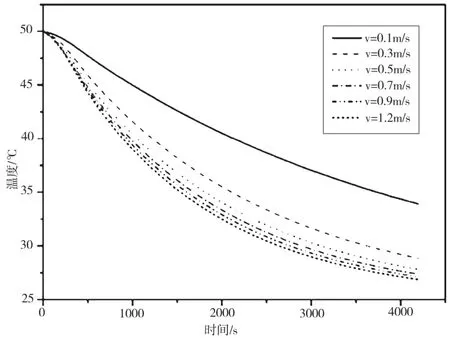
图8 不同流速下PCM表面温度随时间变化关系示意图

图9 不同水速温度分布图

原因也同样可由热阻的概念解释。在热量传递距离、PCM热导率、热流密度q都不变的条件下，增加水的流速，冷却水的换热系数也会随之增加，因此会导致PCM与冷却水之间的温度差逐渐减小，所以PCM的温降也会减小。

2.5 不同影响因素权重分析

由前面的结果分析可知，对PCM表面温度有影响的主要有四个因素，分别为PCM尺寸（A）、水管管径（B）、PCM导热率（C）和水流速（D）。为了进一步分析得到最佳的电池热管理方案，对这四个主要影响因素进行权重分析。

本次权重分析采用正交实验的方法，对四因素均采用3水平，考察的指标为1 800 s时PCM表面的电池温度，并对正交设计结果进行极差分析，得到各因素影响力大小。

表1为四因素不同水平所选取的参数在不同实验条件下所得到的实验结果和极差分析，结果如表2、表3所示。

在极差分析表中，Kij表示任一列上水平号为i（本设计中i=1、2、3）、因素数为j（本设计中j=A、B、C或D）时，对应的试验结果之和。各因素最优水平根据评价指标确定。本次设计中，温度越低，表明效果越好，因此应选取使指标小的水平，即各列Ki中最小的值所对应的水平。极差R=max(K1j,K2j,K3j)-min(K1j,K2j,K3j)，表明了影响力的大小。不同的极差，表明各因素水平的改变对试验结果的影响是不同的。极差越大，表明该列因素在试验范围内的变化会导致试验指标在数值上变化更大，影响力越大。所以，四因素的影响力大小为：PCM尺寸＞PCM热导率＞管径尺寸＞流速。

表1 四因素三水平表

表2 电池温度极差分析表一

表3 极差分析表二

3 结 论

本文重点研究了在水管结合PCM电池散热系统中影响PCM异地散热的主要因素，并对其影响因素进行权重分析，可以得出结论：

（1）利用冷却水流动可有效吸收PCM中存储的热量，保证PCM温度的进一步升高，从而为电动车的持续运行提供基础；

（2）PCM尺寸的增加会降低其表面散热速度，也会增加PCM内部温度不均匀性；水管管径增加，会增加表面散热速度，且速度增长率与其尺寸变化大致呈正比例；增加水流速，在水流速小于0.5 m/s时，可有效降低PCM表面温度；但随着流速的进一步增加，对PCM表面温度影响很小；在PCM导热率较小时，增加导热率会极大增加PCM表面温度降低速度，但随着导热率进一步增加，对PCM表面温度影响逐渐减小。

（3）通过采用正交实验的方法，利用极差分析，可得出四个主要影响因素的影响力大小为：PCM尺寸＞PCM热导率＞水管管径＞水流速。