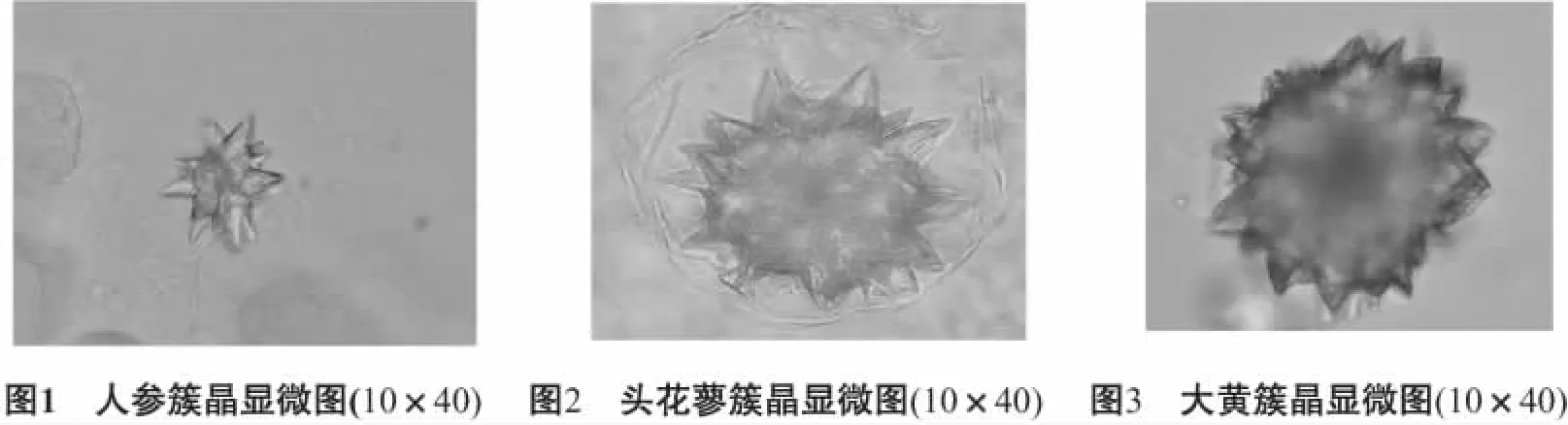
草酸钙簇晶棱角角度用于中药鉴定的研究

贵州中医药大学，贵州 贵阳 550002

有研究显示草酸钙簇晶是由多数菱形的晶瓣组成的[1-4]，菱形晶瓣的棱角(外缘角)清晰可辨。笔者认为，既然菱形晶瓣有棱角，那就有角度，可以测量其角度数据，再运用数学方法运算，求得角度均数值以及上限和下限区间值。那么每个中药品种的草酸钙簇晶棱角是否有特定的均数值，不同的中药草酸钙簇晶棱角均数值是否不同。换而言之，是否可以将中药的草酸钙簇晶的显微形态特征转换成数据特征，是否可以为中药鉴定探索一种新的鉴定方法。基于此，笔者以大黄、人参和头花蓼[5-6]为实验材料开展了相关试验。具体报告如下。

1 仪器与材料

1.1 仪器 Olympus CX41及EX20光学显微镜、数码相机、智能手机、电脑、量角器。

1.2 材料 水合氯醛、氢氧化钠、稀甘油。大黄RheumofficinaleBaill.药材样品A(贵州道真，三年生)，样品B(贵州道真，四年生)，药材样品C(四川南川)；人参PanaxginsengC.A.Mey.药材样品A(吉林集安，五年生)，样品B(辽宁抚顺，五年生)，样品C(吉林集安，四年生)；头花蓼PolygonumcapitatumBuch.-Ham. ex D. Don药材样品A(贵州施秉)，样品B(云南腾冲)，样品C(贵州贵阳)。以上药材样品均经贵阳中医学院中药鉴定教研室周汉华教授鉴定。

2 方法

2.1 数据采集 以10%～20%的氢氧化钠为解离试剂制作解离制片，显微观察草酸钙簇晶，调至清晰后用数码相机或智能手机照相，电脑放大或者打印，用量角器测量草酸钙簇晶棱角(晶瓣顶端角)的角度，记录数据。采集过程中每个样品制片采集10个簇晶样品数据，避免重复采样，大黄、人参及头花蓼三种药材的样品A随机采集500个数据，样品B、样品C各随机采集100个数据。

2.2 数据分析

2.2.1 求证大黄、人参和头花蓼草酸钙簇晶棱角角度均值

2.2.1.1 求取 以各药材样品A的500个数据。使用SPSS软件中均值操作法，分别得到大黄、人参和头花蓼草酸钙簇晶棱角角度均值。

2.2.1.2 证明 以各药材样品B的100个数据、样品C的100个数据，分别使用SPSS软件单样本t检验操作法，检验和证明“(1)求取”得到的大黄、人参和头花蓼草酸钙簇晶棱角角度均值的准确性。

2.2.2 数据分析 将各药材样品A的500个数据两两编组，使用SPSS软件独立样本t检验操作法，根据得到的结果比较和分析大黄、人参和头花蓼草酸钙簇晶棱角角度均值的差异性。

3 结果

3.1 大黄样品A观测数据 见表1。

表1 大黄样品A的500个簇晶棱角的角度 (°)

续表

表1 大黄样品A的500个簇晶棱角的角度 (°)

3.2 大黄样品A簇晶棱角角度均值 中药大黄样品A的500个簇晶棱角角度的均值为63.04°，95%的置信区间的上限为63.98°，下限为62.10°。见表2。

3.3 大黄样品A簇晶棱角角度均值63.04°的准确性检验 见表3～10。

表2 大黄样品A簇晶棱角角度均值

表3 大黄样品B的100个簇晶棱角的角度 (°)

续表

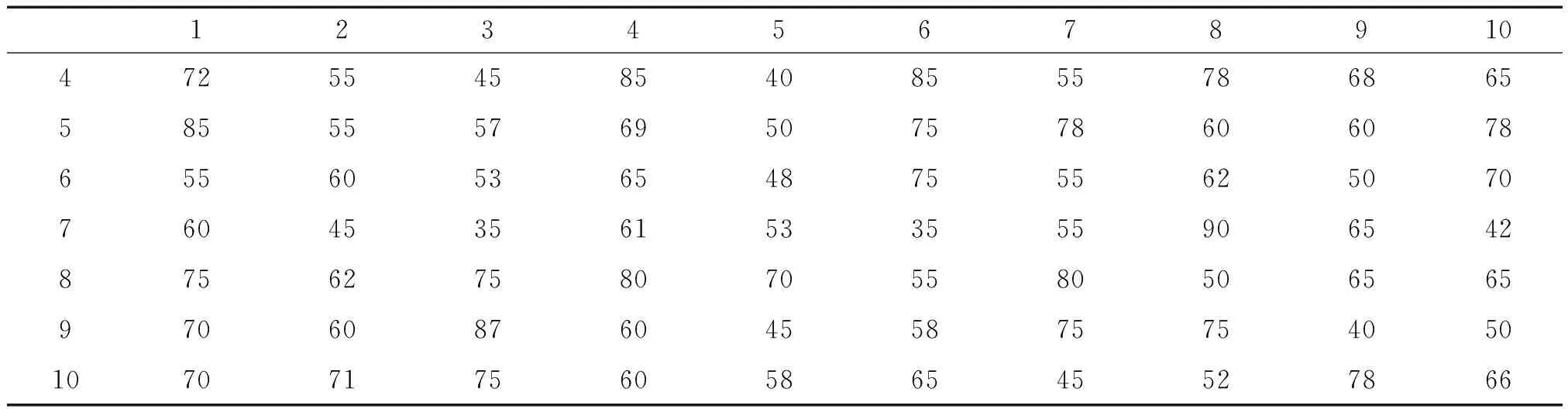
表3 大黄样品B的100个簇晶棱角的角度 (°)

假设H0：μ=μ0，H1：μ≠μ0，μ0= 63.04°，使用SPSS软件单样本t检验操作得到表4、表5、表6的结果。

表4 用Explore对表3数据进行正态性检验的结果

a. Lilliefors 显著水平修正

由表4可知，P=0.514>0.05，可认为大黄样品B簇晶棱角角度服从正态分布。如下进行单样本t检验。

表5 单个样本统计量

表6 单个样本检验

由表6可知，t=-0.257，双侧P=0.798>0.05，按α=0.05水准接受H0，差异无统计学意义，可以认为大黄样品B的100个簇晶棱角角度数据的均值与大黄样品A的500个数据的均值无变化。

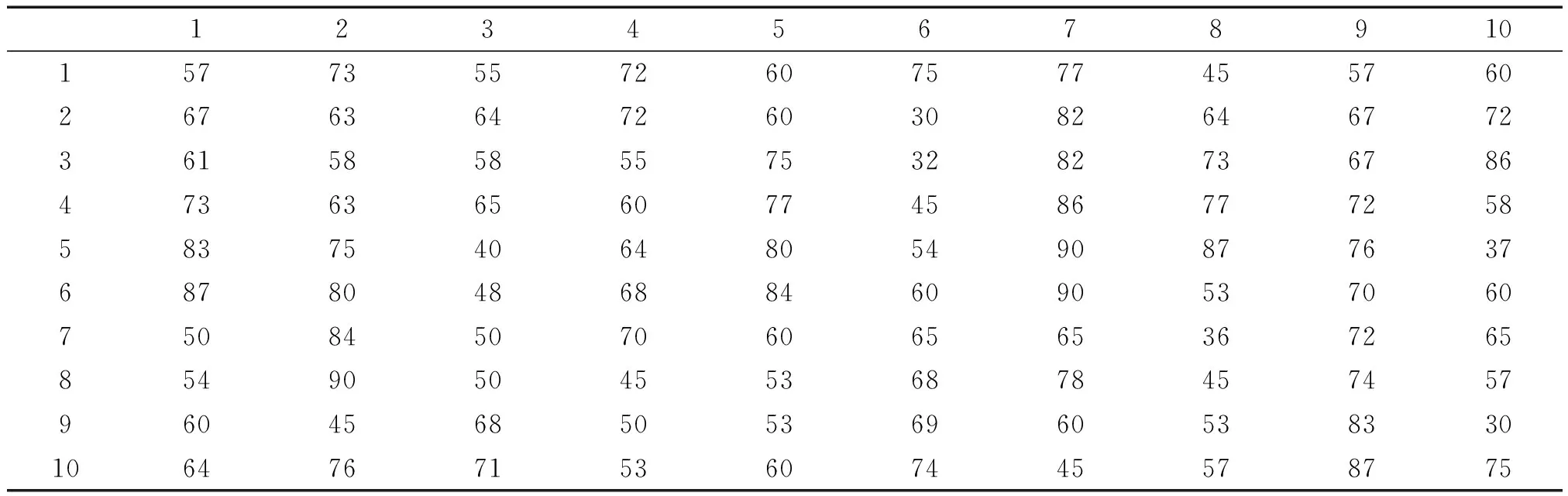
表7 大黄样品C的100个草酸钙簇晶棱角的角度 (°)

假设H0：μ=μ0，H1：μ≠μ0，μ0=63.04°，使用SPSS软件单样本t检验操作得到表8、表9、表10 的结果。

表8 用Explore对表7数据进行正态性检验的结果

*. 这是真实显著水平的下限。

a. Lilliefors 显著水平修正

由表8可知，P=0.166>0.05，可认为大黄样品C簇晶棱角角度服从正态分布。如下进行单样本t检验。

表9 单个样本统计量

表10 单个样本检验

由表10可知，t=0.998，双侧P=0.321>0.05，按α=0.05水准接受H0，差异无统计学意义，可以认为大黄样品C的100个簇晶棱角角度数据的均值和大黄样品A的500个数据的均值无变化。

3.4 人参、头花蓼草酸钙簇晶棱角角度均值及置信区间 见表11。

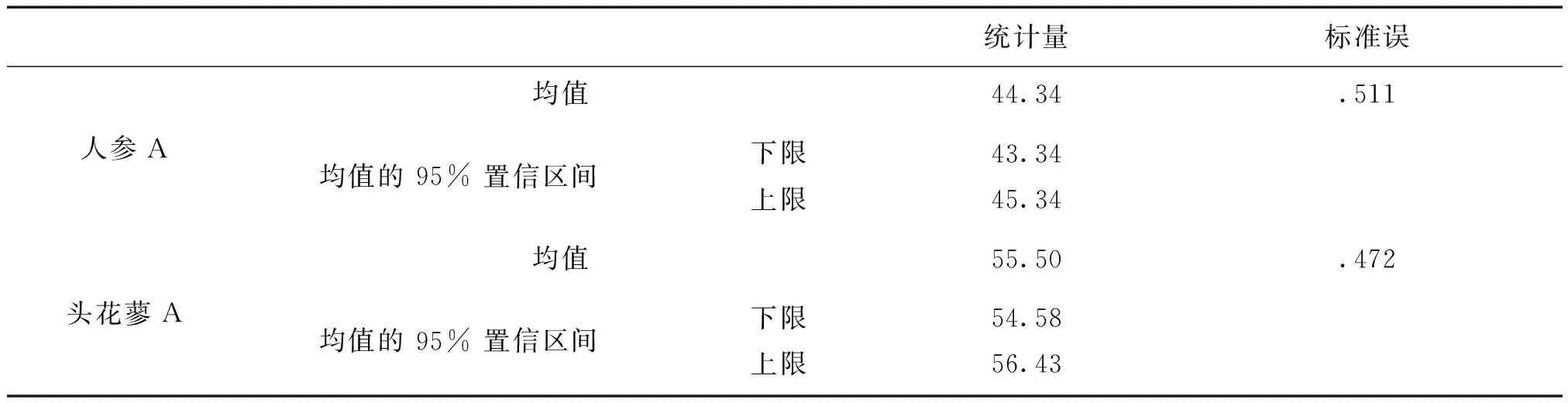
表11 人参、头花蓼草酸钙簇晶棱角角度的均值

由表11可知，人参样品A500个簇晶棱角角度的均值为44.34°，95%置信区间的上限为45.34°，下限为44.34°。头花蓼样品A500个簇晶棱角角度的均值为55.50°，95%的置信区间的上限为56.43°，下限为54.58°。

3.5 大黄与人参、大黄与头花蓼、头花蓼与人参独立样本t检验 见表12～18。

由表12可知，Shapiro-Wilk统计量分别为0.996、0.996、0.995，三组的P值分别为0.250、0.342、0.114，均>0.05，可认为大黄A、人参A、头花蓼A簇晶棱角角度均服从正态分布。如下分别进行两组独立样本t检验。

由表13可知，大黄簇晶棱角的均值为63.04°，人参44.34°。

假设H0：μ1=μ2，H1：μ1≠μ2，其中μ1代表大黄的均值，μ2代表人参的均值。

表12 用Explore对表大黄A、人参A、头花蓼A数据进行正态性检验的结果

表13 大黄、人参簇晶棱角角度数据组统计量

表14 大黄、人参两组独立样本检验

从表14方差方程的 Levene 检验统计量F=2.530，P=0.0.112>0.05，不能认为两组的总体方差不齐；t=26.787，双侧P=0.000<0.01，以α=0.01水准的双侧检验拒绝H0，两组的差异有统计学意义。即大黄均值63.04°与人参均值44.34°有显著性区别，可认为大黄草酸钙簇晶棱角角度的均值明显大于人参。

表15 大黄、头花蓼簇晶棱角角度数据组统计量

由表15可知，大黄簇晶棱角的均值为63.04°，头花蓼55.50°。

假设H0：μ1=μ2，H1：μ1≠μ2，其中μ1代表人参的均值，μ2代表头花蓼的均值。

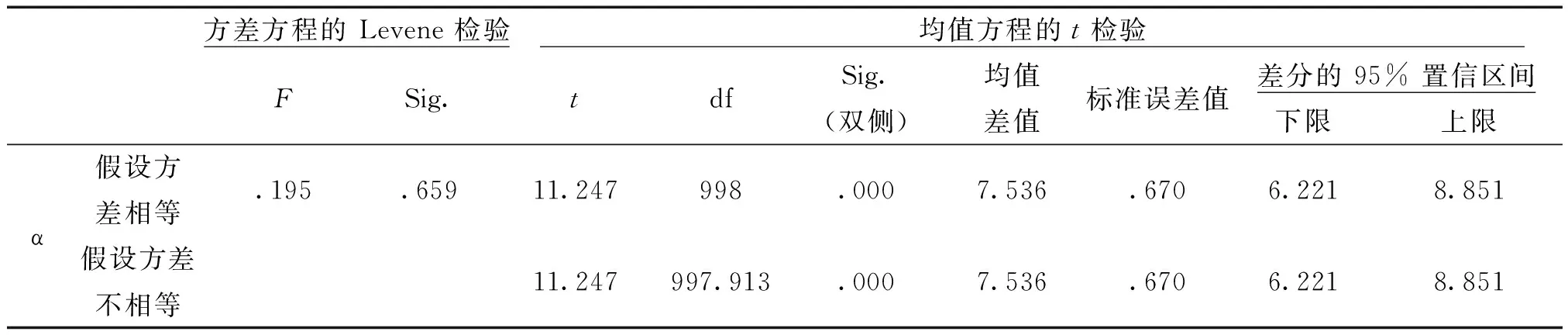
表16 大黄、头花蓼两组独立样本检验

从表16方差方程的 Levene 检验统计量F=0.195，P=0.659>0.05，不能认为两组的总体方差不齐；t=11.247，双侧P=0.000<0.01，以α=0.01水准的双侧检验拒绝H0，两组的差异有统计学意义。即大黄均值63.04°与头花蓼均值55.50°有显著性区别，可认为大黄的簇晶棱角角度的均值明显大于头花蓼。

表17 头花蓼、人参簇晶棱角角度数据组统计量

由表17可知，头花蓼簇晶棱角角度的均值为55.50°，人参44.34°

假设H0：μ1=μ2，H1：μ1≠μ2，其中μ1代表头花蓼的均值，μ2代表人参的均值。

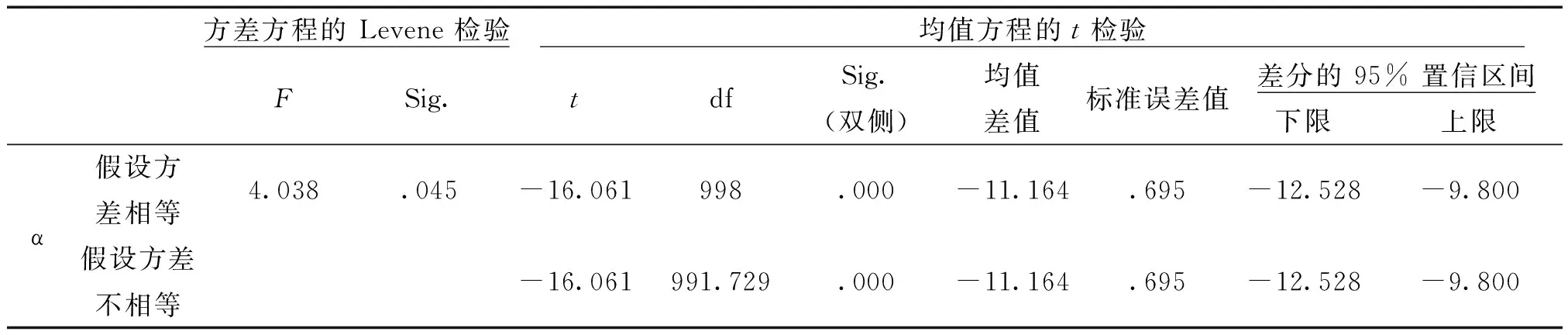
表18 头花蓼、人参两组独立样本检验

从表18方差方程的 Levene 检验统计量F=4.038，P=0.045<0.05，认为两组的总体方差不齐；t=-16.061，双侧P=0.000<0.05，以α=0.05水准的双侧检验拒绝H0，两组的差异有统计学意义。即头花蓼均值55.50°与人参均值44.34°有显著性区别，可认为头花蓼的簇晶棱角角度的均值明显大于人参。

4 讨论

研究表明中药的草酸钙簇晶晶瓣棱角是有角度的，可以测量的。大黄、人参、头花蓼的棱角角度各自有特定的均值数，可以作为大黄、人参及头花蓼显微鉴定的重要参数。研究过程中笔者还对簇晶的晶瓣数进行统计学研究，结果也有特定的均值范围，因此若将簇晶的棱角特点与晶瓣数、大小特征可作为药材鉴定的重要参数。

本研究思路创新点是拟将具体的显微鉴别的形态特征转化为数字、数据，再结合运用数理统计的方法形成显微鉴别的特征数值或常数，作为中药鉴定的依据或参数。研究结果初步证明这个思路是正确的、可行的，提示中药显微鉴别法可以从以形态区别为主要特征的经典思维模式和方法模式向数字化、数据化方向延伸和探索发展。但相关方法还有待进一步研究和完善。