波浪中船舶结构惯性力求解及实际工程应用

傅健

（海洋石油工程股份有限公司，天津 300451）

船舶在海浪中受到环境载荷的影响，作用在船舶的计算载荷主要由船舶的重力、船舶摇荡时产生的惯性力、所受的风力及舷外水压力四部分组成。

结构分析中各项载荷、重力和风力很容易计算和加载，但是摇摆时所引起的惯性力由于跟质量分布和船舶在波浪中的运动状态有关，较为复杂，有必要进行研究探讨[2]。

本文中假定在船舶甲板上方放置一定重量的货物，船舶在波浪中运动状态下，对货物的惯性力计算方法进行了较为深入系统的研究，得出了一套较为简洁的理论计算公式，并应用到实际工程项目中，确保了工程实施的安全性。

1 船舶在波浪中运动的概述

船舶在随机的、波浪方向紊乱的海上航行和作业时，必然会受海浪的扰动产生振荡运动。如果把船作为刚体，则这种运动一般应有六个自由度。图1给出船舶振荡运动的定义。如取o-xyz为固定在船上的右手坐标系；相对于振荡运动的船为固定的右手坐标系O-XYZ[3]。这时船（即o-xyz坐标系）相对于O-XYZ坐标系的六个自由度运动是：

（1）沿三个坐标轴的往复振荡。

X-进退运动； Y-横荡运动；

Z-升沉（或垂荡）运动。

（2）绕三个坐标轴的旋转振荡。

Φ-横摇，绕x轴的旋转振荡；

θ-纵摇，绕y轴的旋转振荡；

Ψ-首尾摇，绕z轴的旋转振荡。

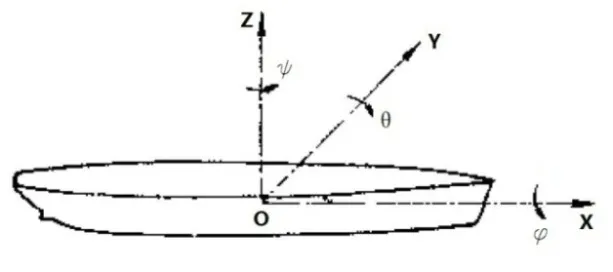
图1 船舶在波浪中振荡运动的定义

上述运动按照图1中所示的箭头方向取正值，与箭头方向相反的取负值。

2 惯性力计算

当船舶在波浪中运动时，固定在甲板上方的货物将随着船舶运动产生很大的加速度，而加速度本身由角加速度和线加速度两部分组成。为了保证货物绑扎固定设计的可靠性以及对货物本身结构的影响，应考虑其加速度产生的惯性力的影响。通常在求解加速度和惯性力时，考虑以下运动组合情况[1]：

（1）横摇+垂荡；

（2）纵摇+垂荡。

取坐标系方向：x轴沿船长方向（由船首指向船尾），y轴指向船舶右舷，z轴垂直向上，原点取在摇摆中心处。

以下主要针对船舶在上述两种组合运动状态下，惯性力计算的详细推导过程，表1为船舶在波浪中的运动状态。

表1 船舶在波浪中的运动状态

2.1 横摇+垂荡

最大横摇发生在共振时候，扰动力的周期与船舶的摇摆周期一致。船舶的横摇方程式为[3]：

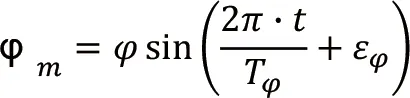
式中：

ϕ：船舶最大横倾角度；

Tϕ：船舶横摇周期；

εϕ：相位差。

当存在着与速度的一次方成正比的阻力时，共振时的位移相角比扰动力的相角落后此时角加速度达到最大值。

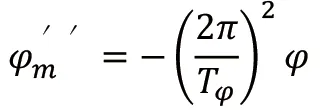
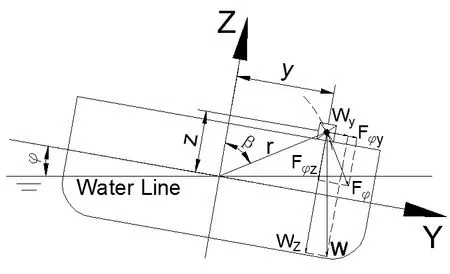
图2 船舶横摇时货物惯性力矢量

图中：

W：甲板货物自重；

y：货物重心至船中纵线的横向距离；

z：货物重心至摇摆中心的垂直距离；

r：货物重心横摇半径。

船舶发生横摇时，甲板货物在小范围绕摇摆中心做圆周运动，切向加速度计算公式如下：

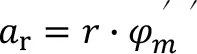
根据图2所示，各参数关系可知：

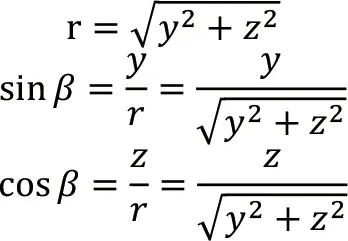
货物由圆周运动产生的切向力为：

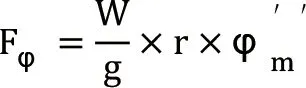
因此，切向力的水平和垂向分量分别为：

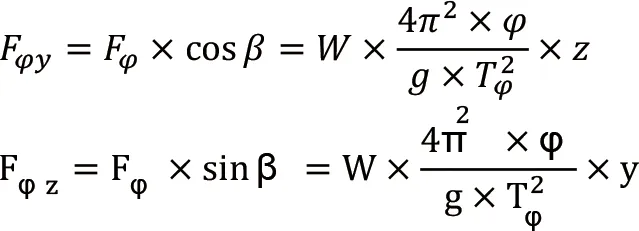
货物重量在y与z方向的分量分别为：

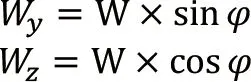
综合以上公式，仅考虑船舶横摇运动时，在船宽方向和垂直方向上的总的惯性力之和：

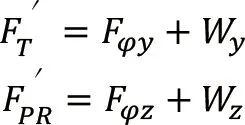
由于船舶在波浪中，发生横摇运动的同时也会存在垂荡运动。考虑垂荡加速度对惯性力的叠加影响，甲板货物在船宽方向和垂直方向的最大惯性力计算公式分别为：

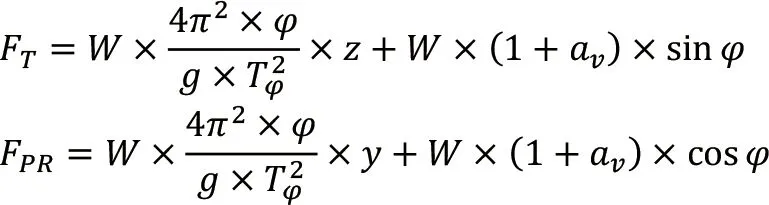
2.2 纵摇+垂荡

最大纵摇发生在共振时候，扰动力的周期与船舶的摇摆周期一致。船舶的纵摇方程式为[3]：

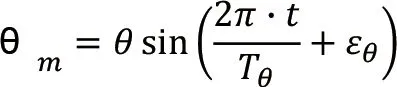
式中：

θ：船舶最大纵倾角度；

Tθ：船舶纵摇周期；

εθ：相位差。

当存在着与速度的一次方成正比的阻力时，共振时的位移相角比扰动力的相角落后此时角加速度达到最大值。

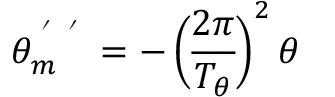
图3 船舶纵摇时货物惯性力矢量

图中：

W：甲板货物自重；

x：货物重心至摇摆中心的纵向距离；

z：货物重心至摇摆中心的垂直距离；

r：货物重心纵摇半径。

同理，船舶在纵摇+垂荡组合运动状态下，甲板货物在船长方向和垂直方向的最大惯性力计算公式分别为：

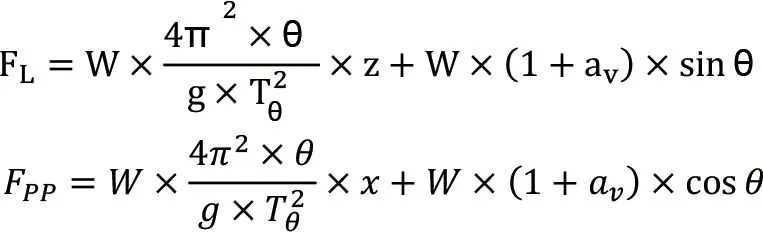
3 惯性力公式实际工程应用

上述惯性力计算公式，通常在海洋工程结构物运输绑扎设计中使用，较为典型的是固定式平台钢桩运输的绑扎固定设计。下面以某国外实际钢桩运输设计工程项目为例，简单介绍上述惯性力计算公式的应用。

该项目中共有两种类型的钢桩，在驳船甲板上的布置及详细重心信息，见图4。

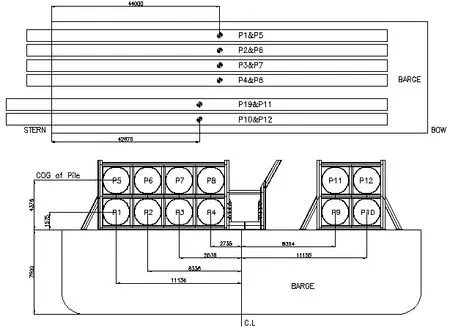
图4 钢桩布置图及重心位置信息

类型1（P1～P8）：重量为323.8吨/根；类型2（P9～P12）：重量为331.4吨/根。

工程项目使用的驳船主尺度为：

船长：110m；型宽：32m；型深：7.5m。

驳船实际在波浪中的运动状态，见表2。

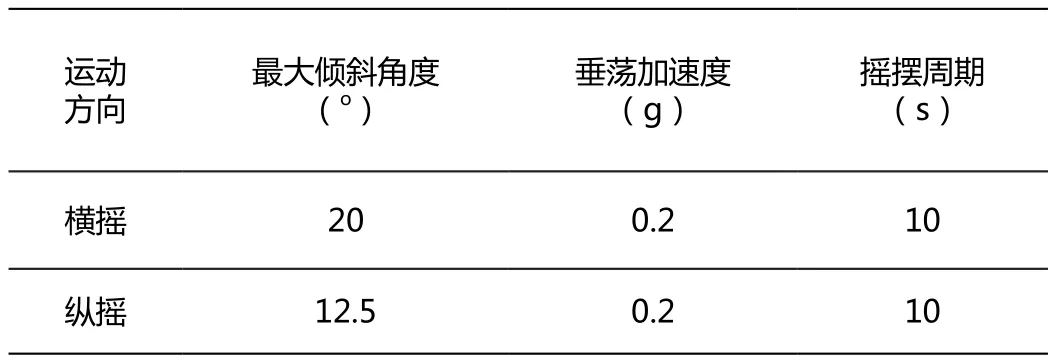
表2 驳船实际运动状态

根据驳船空船重量重心和钢桩重量重心信息，以及驳船舱室压载情况，参考相关规范使用MOSE S软件求解出驳船的实际摇摆中心，详细位置见图5。

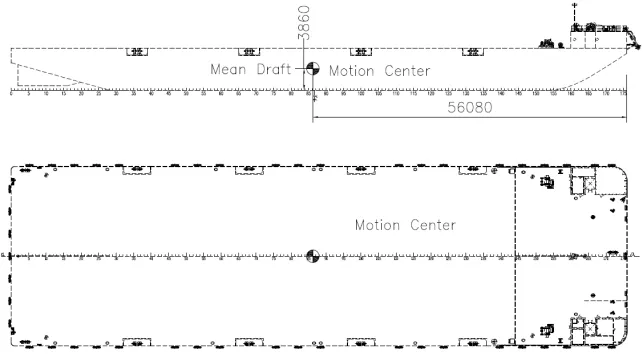
图5 驳船实际摇摆中心

综合上述计算结果，代入到惯性力计算公式中可得：

3.1 横向力

FT-P1/P2/P3/P4=156.638MT，

FT-P5/P6/P7/P8=169.387MT，

FT-P9/P10=160.315MT，

FT-P11/P12=173.363MT。

3.2 纵向力

FL-P1/P2/P3/P4=98.943MT，

FL-P5/P6/P7/P8=106.914MT，

FL-P9/P10=101.266MT，

FL-P11/12=109.423MT。

3.3 垂向力

根据钢桩的布置及重量信息，可以分为6堆，即P1&P5、P2&P6、P3&P7，P4&P8，P9&P11和P10&P12。按照 3中所述的两种工况组合的方式分别计算垂向力，再取两者之间的较大值作为设计载荷。另外，由于钢桩在驳船上的摆放形式为两层，因此计算垂向力时，应将上下两层的钢桩重量求和。根据上述垂向力计算原理，最大垂向力计算结果如下：

3.3.1 横摇+垂荡

FPR-P1&P5=831.654MT，

FPR-P2&P6=806.155MT，

FPR-P3&P7=780.657MT，

FPR-P4&P8=755.159MT，

FPR-P9&P11=825.248MT，

FPR-P10&P12=851.345MT。

3.3.2 纵摇+垂荡

根据上述垂向力计算公式可知，前4堆钢桩（P1&P5、P2&P6、P3&P7和P4&P8）在纵摇+垂荡工况下，其垂向力计算结果相同，即为FPP-1=815.168MT。

后2堆钢桩（P9&P11和P10&P12）在纵摇+垂荡工况下，其垂向力计算结果相同，即为FPP-2=842.049MT。

最后，使用上述计算得到的横向力、纵向力和垂向力结果，进行钢桩固定以及驳船船体强度的校核，确保设计满足相关规范要求。

4 结论

本文对波浪中船舶惯性力的计算方法进行了深入系统的研究，详细地介绍了理论计算方法的公式推导原理，得出了一套较为简洁的理论计算公式。通过实际工程项目的使用，验证了该套惯性力计算公式的可行性，得到了海洋工程行业内的普遍认可，确保了工程实施的安全，并为实际工程的实施提供了理论依据，同时也避免了许多繁琐的计算过程。