基于改进强跟踪ASCKF算法的SINS/GNSS组合对准方法
刘 轶,程旭红,程建华
(1. 海军驻北京地区航空军事代表室, 北京 100073;2. 烟台广电信息网络中心 广电技术部, 烟台 264000;3. 哈尔滨工程大学 自动化学院, 哈尔滨 150001)
0 引言
初始对准是捷联惯性导航系统(Strapdown Inertial Navigation System,SINS)的关键技术之一,对准精度直接影响系统的导航定位精度[1-2]。随着组合导航系统的快速发展,组合对准成为初始对准技术发展的重要方向之一。其中,SINS与全球导航卫星系统(Global Navigation Satellite System,GNSS)的组合对准应用最为广泛。在实际应用中,受限于系统惯性器件自身的测量误差、系统建模误差以及海上环境的恶劣性等因素,SINS/GNSS组合对准系统经惯性系粗对准后方位失准角较大,系统具有较强的非线性、时变性和模型不确定性[3]。因此,在精对准阶段需要建立基于大方位失准角的非线性误差模型,并采用非线性滤波方法实现初始对准。
其中,容积卡尔曼滤波[4-6](Cubature Kalman Filter,CKF)是一种利用三阶球面—径向容积规则对非线性函数进行近似高斯积分的非线性滤波方法。相比于扩展卡尔曼滤波、无迹卡尔曼滤波等,CKF无需计算雅可比矩阵,计算过程相对简单;在滤波过程中不依赖非线性函数的具体形式,适用于几乎任何非线性系统;当系统维数较高时,采用CKF能有效改善滤波精度及稳定性[7]。基于以上优点,采用CKF进行SINS大方位失准角下的初始对准,能够基本解决对准过程中的非线性问题,提高系统的对准精度[8-11]。
海上启动状态下,受各种机动条件的约束以及高海况的干扰,初始对准过程很难在短时间内达到收敛。对此,采用强跟踪滤波(Strong Tracking Filter,STF)技术能够有效改善对准系统的鲁棒性,加强系统对突发状况的跟踪能力[12]。在实际对准过程中,由于外界环境的干扰,系统的噪声统计特性不断变化,通过引入Sage-Husa自适应滤波算法能够实时获取噪声的统计特性,提高系统的自适应能力[13-14]。
综合考虑,提出了一种基于改进强跟踪自适应平方根CKF(改进的强跟踪ASCKF)算法的SINS/GNSS组合对准方法,该方法能够有效改善非线性系统在大方位失准角情况下的对准性能。
1 SINS/GNSS组合对准数学建模
初始对准的关键在于如何获得准确的初始捷联矩阵,其基本原理是利用惯性器件的敏感信息,经粗对准得到一个满足要求的粗略姿态矩阵,在此基础上通过精对准精确估计出实际解算的地理坐标系n′系与理想的地理坐标系n系之间的失准角,并使之趋于0,从而得到精确的捷联矩阵。在SINS/GNSS组合对准过程中,水平对准速度较快、精度较高,系统经粗对准后得到的水平失准角一般为小角度,而方位失准角的收敛速度相对缓慢,粗对准结束时刻方位失准角仍较大,因此需要在精对准阶段建立基于大方位失准角的非线性误差模型。

(1)
其中:
(2)
捷联惯导系统的速度误差方程、姿态误差方程为[15]:
(3)
(4)
基于此,选取合适的状态变量建立如下形式的SINS/GNSS组合对准系统模型:
(5)
忽略垂向,选取状态变量X为
其中,δVE、δVN分别为东向、北向速度误差;δφ、δλ分别为经度、纬度误差;φE、φN、φU为3个方向的姿态误差;εE、εN、εU为3个方向的陀螺漂移。
系统噪声ω为

选取观测量Z为SINS与GNSS二者位置误差的差值,v为量测噪声,h为量测矩阵,由于在此系统中,量测方程为线性,故量测矩阵为
对上述SINS/GNSS组合对准模型进行离散化,得到如下的非线性系统:
(6)
式中,ωk-1是零均值、方差为Qk-1的系统噪声,vk是零均值、方差为Rk的量测噪声,二者为相互独立的高斯白噪声。
2 改进强跟踪ASCKF算法设计
传统的CKF算法是在三阶球面—径向容积规则的基础上,利用一组权值相等的容积点对非线性函数进行近似高斯积分运算,从而得到随机变量的均值和方差[4-5]。
当系统模型不准确或噪声统计特性未知时,采用CKF进行大方位失准角下的初始对准会带来较大的对准误差,甚至引起滤波发散。针对上述情况,提出了一种改进强跟踪ASCKF算法。该算法通过引入改进的强跟踪滤波器和时变噪声统计估计器,能够抑制滤波发散,提高大方位失准角下的对准精度。
2.1 改进的强跟踪滤波器
强跟踪滤波要求输出残差序列时刻保持正交,满足以下要求[16]:
当系统中存在的各种不确定误差较大时,无法保证残差序列γk时时正交,通过在状态协方差阵中引入多重渐消因子矩阵,可以提高新数据在滤波过程中的比重,在线调整滤波增益Kk,以提高系统鲁棒性和对突发状态的跟踪能力。多重渐消因子矩阵λk的求解如下[17-18]:
λk=diag[λ1,k,λ2,k,…,λn,k]
(7)
(8)
其中:
(9)
(10)
(11)
式中,αi可根据先验知识确定,ρ为遗忘因子,0<ρ≤1,通常ρ取0.95;β为弱化因子,取为3。
式(11)中涉及雅可比矩阵的计算,当系统维数较高时,计算过程复杂。因此,本文基于强跟踪滤波的等效描述,采用CKF迭代过程中的状态协方差和量测协方差表示Nk、Mk。
(12)
由式(12)得
(13)
将式(13)代入式(9),则Nk可表示为
Nk=Vk-βRk-
(14)
对于Mk有
(15)
结合式(9)、式(15),将Mk进一步表示为
(16)


(17)
改进的强跟踪滤波器通过在状态预测方差阵的平方根更新中引入多重渐消因子调整滤波增益,避免求取雅可比矩阵,计算更加简便,改善了系统的鲁棒性。
2.2 改进的时变噪声统计估计器
在应用CKF进行组合对准的过程中,涉及系统噪声和量测噪声的协方差矩阵,而在实际情况中是很难准确获得噪声的统计特性。对此,文献[19]中提出一种基于CKF的时变噪声估计器,能够实时估计噪声的统计特性,详见文献[19]中式(45)、式(46):
(18)


(19)
2.3 滤波发散判断
针对新息异常易影响噪声统计特性的问题,基于协方差匹配的原则,引入滤波发散判断
(20)
式中,tr()为求矩阵的迹。若式(20)成立,则式(19)改写为:
(21)
3 改进强跟踪ASCKF算法实现
计算机的截断效应会导致传统CKF在求取容积点的过程中产生较大的舍入误差,影响滤波稳定性。为了降低二次求取过程中舍入误差的影响,采用矩阵QR分解的形式直接求取状态预测阵的分解因子,并结合上述改进的强跟踪滤波器、时变噪声统计估计器,设计了一种改进的强跟踪ASCKF算法,具体实现过程如下:
(22)
2) 利用上一时刻的状态估计误差协方差阵的分解因子Sk-1/k-1计算容积点:
(23)

(24)
(25)
(26)
(27)
6) 重新采样:
(28)

(29)
(30)
(31)
(32)
(33)
式中:
(34)
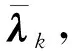
(35)
12) 重复上述步骤6)~10),重新计算容积点,并进行量测更新,得到新的Szz,k/k-1、Pzz,k/k-1、Pxz,k/k-1。
13) 计算滤波增益Kk:
(36)
14) 进行状态更新:
(37)
15) 计算状态估计误差协方差矩阵的分解因子:
(38)
16) 基于以上改进的CKF算法,将式(19)进一步简化为:
(39)

18)k=k+1,依次重复上述步骤,进行下一次滤波。
4 仿真分析
4.1 仿真条件设置
1) 仿真条件初始化:
初始位置:纬度φ=45.7796°,经度λ=126.6705°;精对准过程中,做匀加速运动,初始速度5n mile/h、加速度为0.1g;航向角为45°。载体摇摆运动参数如下:
陀螺仪常值漂移0.003(°)/h,噪声0.0005(°)/h;加速度计零偏3.0×10-5g,噪声5.0×10-6g;仿真时间0.4h。
2) 滤波器参数设置:
状态误差协方差阵初始化:
P0/0= diag{(0.1m/s)2,(0.1m/s)2,(2m)2,
(2m)2,(0.017°)2,(0.017°)2,(0.033°)2,
(0.003(°)/h)2,(0.003(°)/h)2,(0.003(°)/h)2}
系统噪声方差阵初始化:
0,0,(0.0005(°)/h)2,(0.0005(°)/h)2,
(0.0005(°)/h)2,0,0,0}
量测噪声方差阵初始化:
4.2 仿真结果分析
针对以下两种不同大方位失准角情况下的SINS/GNSS组合对准,分别采用传统的CKF和改进的强跟踪ASCKF算法进行初始对准仿真。
情况1:当初始失准角为(0.03°,0.03°,0.35°)时,东向失准角误差、北向失准角误差和方位失准角误差仿真结果分别如图1、图2和图3所示。
情况2:当初始失准角为(0.06°,0.06°,0.95°)时,初始方位失准角明显增大情况下,得到东向失准角误差、北向失准角误差和方位失准角误差仿真结果分别如图4、图5和图6所示。
两种不同失准角情况下,初始对准结束时刻方位失准角误差的大小如表1所示。

Tab.1 Alignment results comparison between CKF and improved CKF(′)
由图1、图2、图4、图5可知,在两种不同的大方位失准角情况下,分别采用传统的CKF和改进的强跟踪ASCKF算法进行组合对准,水平失准角精度差异并不明显。由图3、图6以及表1分析可得,采用改进的CKF算法可将方位失准角的对准精度提高70%以上,对准性能明显改善。
5 结论
针对大方位失准角下的初始对准问题,建立了非线性对准误差模型,提出了一种基于改进强跟踪ASCKF算法的SINS/GNSS组合对准方法。相比较传统的CKF算法,该方法能够明显提高大方位失准角下的对准精度,对后续组合导航系统长航时、高精度导航定位具有重要的实际意义。

