载波相位平滑伪距在GPS/SINS紧组合导航系统中的应用

胡 杰，石潇竹

(1. 空中交通管理系统与技术国家重点实验室， 南京 210007；2. 中国电子科技集团公司第二十八研究所， 南京 210007)

0 引言

捷联惯性导航系统(Strapdown Inertial Navigation System, SINS)的运行不依赖于任何外部信息，也不向外部辐射能量，具有良好的隐蔽性和鲁棒性。但是由于SINS是通过对惯性测量单元(Inertial Measurement Unit, IMU)进行积分而得到载体的运动参数，其定位误差随时间积累，如果不采取其他措施，则不能应用于需要进行长时间导航的运载体，如舰船、飞机和军用车辆等。全球定位系统(Global Positioning System，GPS)具有定位精度高且误差不随时间积累等优点，因此利用GPS测量值对SINS误差进行校正是目前常用的一种组合导航方法[1-2]，已经被广泛应用于航空航天、测绘等军用和民用领域，能够连续提供运载体的速度、位置和姿态信息，具有精度高、抗差性强等优点。

GPS与SINS的组合一般可以分为松组合、紧组合和深组合三种方式，其中深组合需要读写GPS接收机内部信号跟踪环路软件的相关量，计算过程较为复杂，而松组合与紧组合是目前常用的组合方式。与松组合相比，紧组合利用伪距、多普勒频移等测距信息进行误差校正，其参与组合的测量值之间的相关性较低，因此性能更优。文献[3]研究了惯性卫星紧组合导航系统，详细推导了紧组合导航系统的伪距、伪距率误差模型；文献[4]提出了一种惯性/GPS伪距/伪距率组合导航算法的实现方法，并利用实测数据进行了离线仿真；文献[5]搭建了硬件系统，并进行了车载实验。但是由于一个C/A码的波长约300m，而测量噪声误差一般为波长的1%，即为3m，同时多路径误差会影响伪距测量精度，所以这种组合方式定位精度相对较低。

载波相位测量虽然含有整周模糊度，但是其非常平滑且具有较高的测量精度，如果把高精度的载波相位测量应用到组合导航系统中，则导航精度将会得到进一步提高。载波相位平滑伪距是一种利用载波相位平滑特性对码伪距进行滤波的方法，该方法不需要解算整周模糊度、不需要参考站信息，能够有效降低码伪距噪声[6-7]。Hatch滤波[8]是目前应用最为广泛的一种相位平滑伪距算法，文献[9]对Hatch滤波器进行了研究，并比较分析了有无滤波前后GPS单点定位精度，结果表明，经过Hatch滤波后，伪距单点定位精度得到提高。根据上述文献分析可知，在GPS/SINS紧组合导航系统中，如果把伪距与载波相位的优势结合在一起，利用相位平滑后的伪距对SINS误差进行修正则可以进一步提高组合导航系统的精度。本文对Hatch滤波器平滑原理进行了分析，并推导给出了GPS/SINS紧组合滤波模型，包括系统状态方程和观测方程，同时为了减小Kalman滤波器观测向量维数，提出了一种基于最大四面体体积法的卫星几何精度因子(Geometric Dilution Precision，GDOP)计算方法，该方法不需要矩阵的求逆运算，可以减小运算量。最后通过车载实验对本文所提出方法的可行性进行了验证，结果表明载波相位平滑伪距后能够进一步提高GPS/SINS紧组合导航精度。

1 GPS/SINS紧组合滤波模型

在GPS/SINS紧组合滤波模型中，系统的状态方程由SINS的误差状态和GPS的误差状态组成，观测方程由SINS导航结果推算得到的伪距、伪距率与GPS观测得到的伪距、伪距率相减得到。

1.1 紧组合状态方程

SINS以东北天地理坐标系为导航坐标系，SINS的主要误差由位置误差、速度误差、失准角、加速度计常值偏置以及陀螺常值漂移组成，系统状态方程可以写为

(1)

式中：FI(t)为系统的状态转移矩阵，GI(t)为系统的噪声矩阵，WI(t)为系统的过程噪声矢量，XI(t)为系统的误差状态矢量，具体表达式如式(2)所示

(2)

GPS状态参数通常取2个与时间相关的误差δtu和δfu，其中δtu为接收机时钟偏差，δfu为接收机时钟频漂，它们的状态方程分别为：

(3)

式中：β为误差相关时间，wtu、wfu为相应的驱动噪声。

将式(3)写成矩阵形式，即为

(4)

合并式(1)和式(4)可以得到GPS/SINS紧组合状态方程

(5)

根据文献[10]，可得FI(t)、FG(t)、GI(t)、GG(t)的具体表达式，其中WI(t)和WG(t)为零均值高斯白噪声。

1.2 紧组合观测方程

1.2.1 伪距差观测方程

根据SINS力学编排方程可以得到载体的位置为(xIyIzI)T，由卫星星历可以确定卫星的位置为(xsyszs)T，从而可以得到伪距ρI为

(6)

式中：j表示计算得到的第j号卫星伪距。

将式(6)在相对于载体位置坐标真值(xyz)T处进行泰勒级数展开，取其一次项，则有

(7)

(8)

卫星接收机测量得到的与第j号卫星之间的伪距可以表示为

(9)

由式(7)和式(9)可以得到伪距差观测方程为

(10)

1.2.2 伪距率观测方程

载体相对于GPS卫星存在相对运动，对式(6)求导，则可以得到SINS给出的载体速度相对于该卫星j之间的伪距变化率为

(11)

接收机测得的伪距率为

(12)

由式(11)和式(12)可以得到伪距率观测方程为

(13)

1.3 四面体选星法

选择最佳几何分布卫星星座通常需要遵循2个基本原则，首先观测卫星的仰角不能小于10°，其目的是减小大气折射等造成的误差，然后是确保所选择卫星星座的GDOP具有最小值[11]。本文给出了一种四面体选星法，该方法选择组成的四面体体积最大的4颗可见星座参与导航计算。

(14)

式中：S为底面积，h为通过另一个顶点在该面上的高。

为方便计算S和h，定义以下3个变量hpx、hpy、hpz为：

hpx=(y3-y2)(z4-z2)-(z3-z2)(y4-y2)

hpy=(z3-z2)(x4-x2)-(x3-x2)(z4-z2)

hpz=(x3-x2)(y4-y2)-(y3-y2)(x4-x2)

则有：

(15)

(16)

将式(15)和式(16)代入式(14)，即可计算得到四面体的体积。计算所有不同组合情况下的四面体体积，从中选择体积最大的四面体，则对应的4颗星即为最佳可见卫星。

虽然用四面体体积法计算GDOP减少了运算量，但是当可见卫星较多时，将所有的可见卫星进行全遍历，运算量依然很大。以9颗星为例，最大四面体体积法一个历元内需要计算GDOP的次数为126。

对于高仰角的卫星，其电离层以及对流层对伪距的影响相对较小，因此可以首先选择一颗仰角最大的天顶星，在剩余的可见卫星中进行遍历，选择另外的3颗卫星，然后按式(14)、式(15)计算寻找最优的卫星组合，这样在一个历元内所需要计算GDOP的次数为56，明显减小了运算量。

选择了一个历元内最佳的4颗卫星后，可以得到系统的观测方程

(17)

2 载波相位平滑伪距原理

利用精确、平滑的载波相位测量值对粗糙但无模糊度的伪距进行平滑是目前GPS接收机常采用的一种处理手段，在历元k时的伪距观测方程如式(18)和式(19)所示[12]：

(18)

(19)

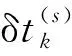
假设接收机一直锁定载波，无载波失锁和失周，则载波相位测量值中的整周模糊度N在各个时刻保持不变，分别对其相邻2个历元的伪距和载波相位进行相减，结果如式(20)和式(21)所示：

(20)

ΔTk+λΔεφ,k

(21)

式中：差分量Δρk与Δφk的定义分别为：

Δρk≡ρk-ρk-1

(22)

Δφk≡φk-φk-1

(23)

由式(20)和式(21)可知，当电离层延时变化量ΔIk很小时，那么伪距变化量Δρk与以距离为单位的载波相位变化量λΔφk理论上应该是相等的，但是前者包含的误差Δερ，k较大，通常是后者误差量λεφ,k的上百倍。由于伪距变化量Δρk与积分距离差λΔφk近似相等，所以组合这两种测量值可以得到一种既无模糊度又相对平滑的距离测量值，如式(24)所示：

(24)

式中：ρs,k为k时刻平滑后的伪距值，ρs,k-1为k-1时刻平滑后的伪距值，M为平滑时间常数，一般取值在20～100个历元(s)之间。

由于GPS导航星座的变化、障碍物的遮挡、接收机的运动等原因，可见星的变化与周跳现象时有发生，在利用式(24)进行噪声平滑滤波时需要对这些特殊情况进行处理以保证最终的平滑效果。

根据式(20)与式(21)分析可知，伪距与载波相位测量之间有如下关系

λ(φk-φk-1)≈ρk-ρk-1

(25)

所以可以采用如下的周跳处理方式，令

temp=|λ(φk-φk-1)-(ρk-ρk-1)|

(26)

式(26)体现了相邻2个历元间的载波观测量的连续性，称为载波差量。将该量作为k时刻是否发生周跳的判决依据。

图1所示为28#卫星一段实测数据载波差量曲线，此过程未发生周跳，由图可知，载波差量变化范围在±0.3m以内，而当有周跳现象发生时，载波差量的值会发生突变，依据此规律，可以确定出周跳判断门限值，本实验选择的周跳门限值为3m。

在该平滑算法中，当载波差量超出周跳门限值时，认为该时刻发生了周跳，此时对平滑器进行重置，使用该时刻的伪距测量值ρ1作为平滑初值，即

ρs,1=ρ1

(27)

图2所示为伪距平滑前后的一个实例。由于伪距值很大，为了显示平滑效果，图中的点画线表示由式(22)计算出的伪距差分量Δρk，图中的另一条曲线是相应的载波相位平滑伪距ρs,k的差分量Δρs,k。

3 验证实验与分析

惯性数据与GPS数据采集设备主要包括：光纤陀螺捷联惯导系统(Fiber Strapdown Inertial Na-vigatien System，FSINS)、高性能商用级GPS接收机、实验车、便携式电脑以及其他相关设备等，车载实验车如图3所示。FSINS是自主研制的一款基于光纤陀螺的捷联惯性导航系统，其IMU由3个光纤陀螺和3个石英挠性加速度计组成，精度指标如表1所示，GPS接收机具有原始数据输出功能，其伪距、伪距率以及载波相位等性能指标如表2所示。

参数项参数值陀螺常值漂移/[(°)/h]≤0.01陀螺角度随机游走/[(°)/h1/2]0.005加速度计常值偏置/μg≤100加速度计随机白噪声标准差/μg200采样频率/Hz200

表2 GPS接收机主要技术参数

车载实验地点为航天科工集团某研究院内的某一条规划路线，如图4所示，图中A点为实验起始点，G点为实验结束点，控制好车辆行驶速度，一次实验持续时间大致为20min，进行了多次验证实验，取其中2组典型数据分别采用离线验证方式对有无载波相位平滑情形下的紧组合导航精度进行分析，离线验证实验平台构建如图5所示。

方案1：GPS/SINS伪距紧组合导航；

方案2：GPS/SINS相位平滑伪距紧组合导航。

对2组数据的GPS信号质量进行分析，其中第一组实验数据GPS信号稳定，接收到的可见卫星数量稳定在9～11颗左右；而第二组实验数据GPS信号在实验第360～570s之间出现一次较为严重的遮挡，可见卫星的数量小于4颗。

图6～图8所示为第一组实验数据3个方向上的位置误差对比曲线，其中蓝线为平滑滤波前的位置误差，红线为平滑滤波后的位置误差，表3所示为平滑前后3个方向的位置误差标准差。

由图6～图8可以看出，当利用载波相位对伪距进行平滑后，3个方向上的位置误差更加平滑，位置误差振荡幅度明显减小，这说明平滑后的伪距提高了GPS/SINS紧组合导航精度，同时由表3给出的位置误差标准差进一步说明了该方法的正确性。

图9～图11所示为第二组实验数据3个方向上的位置误差对比曲线，可以看出，当可见卫星个数小于4颗时，GPS/SINS紧组合位置误差变大，但是载波相位平滑算法依然能够减小伪距噪声对定位精度的影响。

均方根值(Root Mean Square，RMS)是一组统计数据的平方和的平均值的平方根，能够形象地表征数据精度变化。图12所示为第一组实验数据的X轴向位置误差的RMS随时间变化曲线，表4所示为有无载波相位平滑前后3个方向紧组合导航定位误差的RMS值对比，由图12和表4可以看出，经过载波相位平滑伪距后，定位精度可以提高40%以上。

RMS/mXYZ平滑前0.561.711.17平滑后0.271.160.58

4 结论

本文对GPS/SINS紧组合导航技术进行了研究，首先给出了GPS/SINS紧组合状态方程和量测方程，在量测方程确定过程中提出了一种四面体选星法，该方法不需要对矩阵进行求逆，具有运算量低的优点。然后为了减小伪距噪声误差对组合导航精度的影响，引入Hatch滤波器，利用高精度载波相位对伪距进行平滑，在伪距平滑过程中给出了一种工程中易于实现的周跳探测方法。最后利用车载实验数据对本文所提出的方法进行了验证，实验结果表明，载波相位平滑伪距后其位置误差的均方根值相比平滑前减小了40%，提高了组合导航系统的定位精度。