教学中的“对症下药”
常建丽


摘 要:在我们的数学教学中经常会出现这样的现象,老师总觉得给孩子们已经讲的思路非常清晰、非常明白,但孩子们仍然不理解,不会做;有些当时会做了,过一段时间就又不会啦。我们在埋怨学生的同时,是否深究过其中原因呢?其实最根本的原因是因为在这道题中有某一个知识点,在孩子们的思维中存在困惑,搞不懂、不明白。如果你把这个症结真正的为孩子们解开,问题也就迎刃而解了。在五年级上册多边形面积这一单元教学中,我就遇到了这样的问题。
关键词:教学;平行四边形
在一次单元检测中,试卷中有这样的一道填空题:在平行四边形ABCD中,(如图1)。
AB=6厘米,DF=8厘米,DE=4厘米,求平行四邊形ABCD周长是( )厘米,面积是( )平方厘米。
这道题,全班的正确率只有百分之十左右。因为是共性问题,我便在班里统一讲解:要求周长,必须知道BC边的长度,题中给出了DE 长4厘米,而DE是BC边上的高,如果知道了平行四边形ABCD的面积就可以用面积除以4求出BC边的长度。而AB=6厘米,且DF=8厘米,且DF是AB边上的高,所以用6×8可以求出平行四边形ABCD的面积,进而再用面积除以4就算出了BC边的长度为12厘米,进而利用(12+6)×2,就可以求出平行四边形的周长。我自认为思路已经讲的非常清晰,孩子们应该都能够理解掌握了,但是在检查孩子们的改错情况时,才发现有相当一部分的答案仍然是错的。我很郁闷,不知问题出在什么地方。于是我找过来一个孩子当面询问,当问及是否理解、是否会做时,孩子竟然面露难色的告诉我说:老师,我没听懂,你说用6×8可以求出平行四边形ABCD的面积,可是为什么呀?为什么用6×8可以求出平行四边形ABCD的面积呢?DF和AB边啥关系呀?我说“DF是AB边上的高啊。”那学生就说:“为什么说DF是AB边上的高呢?DF有一部分跑到了平行四边形的外部,它怎么会是AB边上的高呢?”此时我才恍然大悟,原来孩子们并不是听不懂这类题的解题思路是什么?而是在思维深处,他不理解DF是AB边上的高。正是因为不理解,所以孩子们在做题时很难找出二者之间的关系,当然也就无从解决问题了。此时我心里豁然开朗,知道了问题所在。看来要想真正的解决这个问题,必须让孩子们深刻的理解,DF是AB边上的高。于是我就在这一点上下足功夫,然后再解决问题。当时我采取了以下的教学策略:
第一步:让学生从定义中理解什么是平行四边形的高。(从平行四边形一条边上的一点到它的对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。)
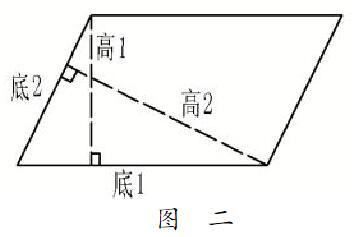
第二步:练习画平行四边形两种不同的高(如图2)。
第三步:我把平行四边形进行变形再变形,让孩子们画平行四边形两种不同的高。让孩子们亲身经历当平行四边形倾斜足够角度时,高会出现一部分在外部的现象(如图3)。
第四步:再讲这道题,让孩子们自己说DF是什么?那么这个题的思路应该怎么做。
经过这一番处理,孩子们才算真正明白了这个题的解题思路,也才达到了真正的理解掌握。看来孩子们之所以认为这道题比较难,不是不会分析,而是对这种特殊不常见的高没有一个清醒和深刻的认识。在教学中,如果我们把孩子们心中的困惑真正的给他抽丝拨茧,理清楚,有针对性的去讲解,对症下药,可能会事半功倍。反之老师讲到黔驴技穷,孩子们仍然是一头雾水。
由此可见,我们在实际教学中,不要盲目的去给孩子们讲题,而是要先做调查分析,找到孩子们的困惑点在哪里,解决了困惑,难题也就迎刃而解了。

