光电经纬仪多数据源融合控制策略

唐自力， 周媛媛， 周铁军， 刘 彪

(华阴兵器试验中心，陕西 华阴 714200)

0 引言

为了适应不同目标特性及测试环境的需求，新一代光电跟踪设备在结构上采用组合式结构，电视、红外、紫外、激光、雷达、微光技术等多种传感器灵活搭配，在测量中发挥各自的优势，实现测量数据的互补偿、互校准，这样的光电测量设备理论上可以对目标进行大时段的饱和跟踪，但在实际应用中，采用手动和按优先级实时切换的多传感器控制策略，会导致跟踪轨迹不够平滑，切换点处出现数据跳变，带来较大的截断误差，致使速度参数出现剧烈的振荡，分析原因主要是融合控制策略简单，融合算法落后。已有的研究主要着重数据融合的理论研究，真正用于光电跟踪融合控制的研究和工程应用较少。本文系统地分析了多数据源融合跟踪的环节与要素，设计出完整的控制流程和有效的融合模型，规划出具有强实时性指标要求的融合结构和融合策略，对提高跟踪可靠性、延伸外弹道测试距离以及保证全弹道数据录取的完整度都具有重要意义。

1 融合控制流程

多源数据融合简称数据融合，也称多传感器信息融合，数据融合在解决探测、跟踪和目标识别等问题上具有许多优良性能[1-3]：增强了系统的生存能力；在有若干传感器不能利用或受到干扰，或某个目标不在覆盖范围内时，总还会有一部分传感器可以提供信息，使系统能够不受干扰地连续运行、弱化故障，并提高检出概率，增加了可信度；一部或多部传感器能确认同一个目标或事件，减少信息的模糊性，降低目标或事件的不确定性，改善系统的可靠性。

数据融合控制流程为：1)输入各传感器的当前观测值及前5帧的融合值和估计值；2)计算椭圆跟踪门规划关联区域；3)剔除野值；4)构建最优融合方案(分时分级)；5)计算各层各级融合加权因子；6)融合计算；7)输出融合位置(合成角)参数。

2 基于模糊集理论的加权融合模型

在多信源对同一个状态进行测量时，常采用加权融合的方法[4]，由于加权融合方法形式简单、计算量小、可靠性高，是目前实时融合系统中的主流方法。

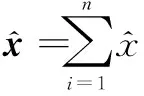
(1)

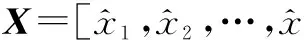
(2)

融合算法最关键的就是加权因子的确定，目前工程上应用较广泛的是最小均方误差方法[5]。利用单模跟踪数据，在权值的最优分配原则下，用自适应加权平均法进行融合。

最小均方误差最小时的加权因子为

(3)

最高精度为

(4)

则融合后的测量估计值为

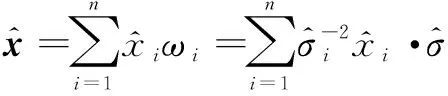
(5)

实际应用中，各传感器的实时动态精度模型是很难准确构建的，像移误差、滞后误差、轴系变形误差、天气环境、布站位置等都必须考虑，才能确定合理的权值。一般情况下，工程上都是用静态精度近似地确立跟踪器的权数，这种情况严重制约了该方法的应用效果。

为了规避常规最小均方误差加权融合算法对各数据源精度模型的苛刻要求，本文从集合统计学的角度构建权值，提出了用基于模糊集理论的隶属度函数来构造融合加权因子的算法。该方法充分考虑到多个传感器的信息冗余和信息熵水平问题，提高跟踪精度和跟踪可靠性，算法原理如下。

一个参数由于采用多个传感器进行探测，可以得到多个样本观测值x1,x2,…,xn。

设多个样本观测值的相对距离为

dij=xi-xj。

(6)

dij的值越大，说明两个测量数据的差别越大；dij的值越小，说明两个测量数据相互支持。为了统一量化处理，利用模糊集理论中的隶属度函数定义置信度函数为

rij=1-2arctan(dij)/π

(7)

式中：dij越小，rij越大；当dij为无穷大时，rij的值为0；当dij为0时，rij的值为1。rij只能反映第i个测量数据与第j个测量数据之间的支持度，不能反映与其余测量数据的支持度[6]。设ωi表示xi被其他测量数据的总体支持度，ωi越大，说明xi被其他测量数据的支持程度越高，越接近于真实值，由此将rij写成R=(rij)n×n。

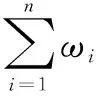
W=RA

(8)

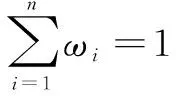
ωi=ai/(a1+a2+…+an)。

(9)

联合式(8)和式(9)，求解可得到ai(i=1,2,…,n),

则融合之后的观测数据为

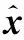
(10)

3 分时分级融合结构和剔野值策略

在上述融合模型的实际应用中，有时会出现某一个传感器的输出信息异常，如果不加取舍地参与到融合计算中，往往会造成融合结果的离散，为了进一步提高融合效果，分离随机误差所带来的影响，本文提出了分时分级融合和野值剔除的策略。

唐自力等： 光电经纬仪多数据源融合控制策略

3.1 分时分级融合策略

理论上，融合了全部可行方案的外测弹道应是精度意义上的最优弹道。然而实时系统中，全部可行的方案参与融合计算，有以下几点困难[7]：

1) 整个系统计算量陡增，系统开销增大，隐藏着很多不确定性，这对强实时性系统而言存在着很大的风险；

2) 不同来源的测量数据，不加取舍地进行单纯性融合，不考虑传感器之间在时间和空间上的互补性和冗余性，反而降低了融合精度；

3) 实时程序对时间点不连续以及断点的判定和处理困难增加。

基于以上考虑，实际系统中采用分时分级融合结构进行分时段、分类型、分层次的融合[8]，以简化处理程序。即融合计算的方案根据时间段和类型进行划分，在每一个时段按信息质量高低和重要程度把参与融合的传感器进行排序分级，依次对每一级传感器的数据进行多级融合，直至完成该时段全部传感器的融合。

本文以某光电经纬仪为例具体阐述分时分级融合的融合结构。该设备参与跟踪控制的数据源主要有可见光测量电视、红外捕获、红外测量、外引导数据和预测滤波数据。具体地，将当前弹道轨迹分为3个时间段，即低空发射段、高空飞行段和低空落地段。在低空发射段，一般以红外捕获为主，外引导数据次之，如图1所示，低空发射段的融合方案，可以充分提高捕获阶段的捕获概率、减少捕获时间以及解决低仰角跟踪情况下背景噪声的随机干扰问题；高空飞行段的融合方案提高了跟踪精度；低空落地段的融合方案减少了地面干扰对目标中靶情况的探测。经过这样的分时分级融合处理之后，每一级的融合都可以保证一定的冗余信息，有利于提高跟踪性能。

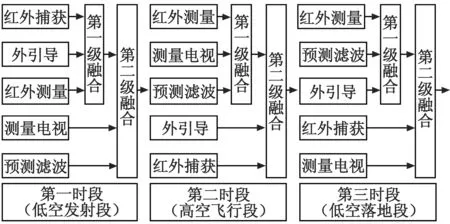
图1 分时分级融合策略图Fig.1 Time-sharing hierarchical fusion strategy

3.2 剔野值策略

在目标跟踪过程中，即使是高精度的测量设备，由于严重噪声干扰、信号丢失、虚假信号等多种偶然因素的综合影响或作用，其采样数据集合往往包含1%～2%有时甚至多达10%～20%(例如目标在遮挡、点火和熄火或者设备故障时)的数据严重偏离目标真值，这部分异常数据为野值，会对之后的融合处理造成一定的影响，因此有必要在进行信息融合之前进行滤除。本文采用一种自适应可变跟踪门的关联区域设计方法对融合前的野值进行剔除，以及对参与融合的信息源进行分级排序[9]。

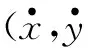
图2 椭圆跟踪门的构建示意图Fig.2 Structure map of elliptical tracking gate

为了方便起见，可以只计算长轴a，通过一个选定的比例因子kp来确定短轴b的大小，算式为

(11)

式中：t为采样时间；θ为椭圆跟踪门长轴的方向角；Di为本航迹在此时刻之前第i帧的残差范数；Nr为选择的相关时间帧数；kr为置信度因子。一般取kp为0.35～0.65；Nr为2～4；kr为3～5。这样就可以得到椭圆跟踪门方程为

(12)

其次，数据关联策略采用最小残差范数

(13)

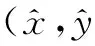
4 试验数据分析

对以15°射角发射的某火箭弹，使用某光电经纬仪进行观测。4路跟踪器：测量电视、红外测量、红外捕获和外引导同时记录实时跟踪数据，融合前后的跟踪误差如图3所示。图中，纵轴值为0的中心线代表真值为事后交会的弹道投影到点位的指向角度，灰色区域代表融合结果与真值的差值，其他颜色分别代表测量电视、红外测量、红外捕获和外引导以及预测滤波工作方式下的跟踪情况，从图中可以明显地看出，融合后的跟踪误差是最小的。

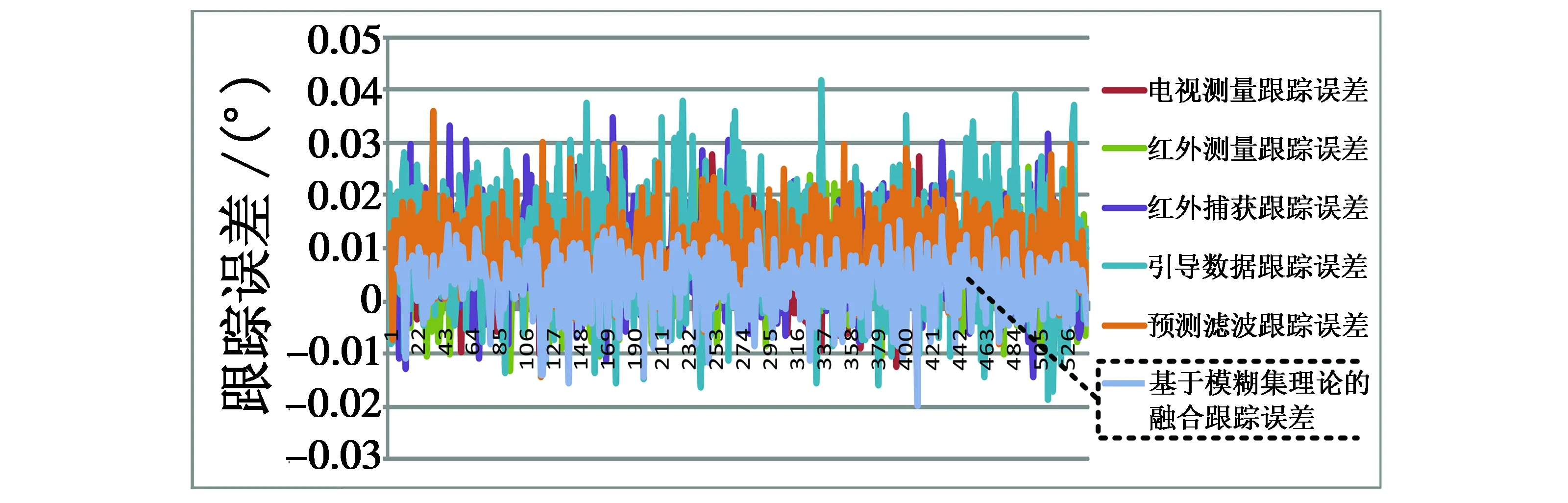
图3 融合前后的跟踪误差Fig.3 Tracking error before and after fusion

并且经过分时分级融合和剔野值策略的应用，融合数据均方误差变小，如表1所示。

表1 融合前后的跟踪误差统计表

同时,如图4所示，速度曲线变得平稳，尤其是对速度参数精度的改善更为明显。

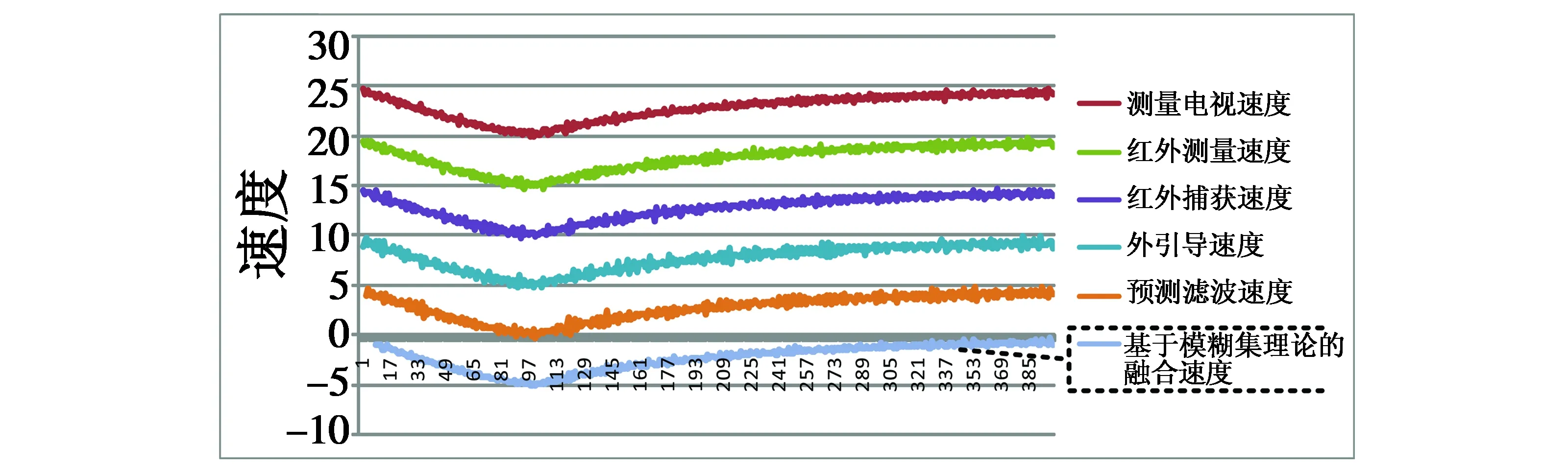
图4 融合前后的速度曲线Fig.4 Velocity curves before and after fusion

为了更好地验证基于模糊集理论的融合加权模型的有效性，对两种加权融合模型的融合效果进行了比较，如图5所示，红色区域代表最小均方误差加权融合的融合误差，该方法误差较大。而基于模糊集理论的加权融合方法，是立足于样本值之间的距离，相当于对测量值的系统差进行了消减，从而改善了融合精度。

图5 两种融合模型的融合效果比较

如图6所示，对切换和融合处理结果进行了比较，红色曲线代表采用切换技术形成的一条混合轨迹，数据曲线不够平滑，在图中切换点第11～16帧数据之间出现了台阶跳，带来较大的截断误差，而融合曲线都很平滑，没有出现数据跳变的问题。

图6 切换和融合处理结果比较Fig.6 Results of switch and fusion processing

5 结束语

本文提出的多数据源融合控制策略具有以下特点：1) 基于模糊集理论的加权融合模型，规避了常规最小均方误差加权融合算法对设备精度模型的苛刻要求，从集合统计学的角度构建权值，从而能够更加有效而精确地实施融合控制；2) 具体实施时提出了一种自适应可变跟踪门的关联区域设计方法对信息源进行分时分级融合和野值剔除的策略，更好地体现了融合控制算法的自适应性、有效性和实时性。

上述特点使本文提出的基于模糊集理论的隶属度函数构造加权因子的融合模型、分时分级融合结构的设计理念，在智能控制领域具有广阔的应用前景。