基于自适应动态规划的一类非线性系统的容错控制器设计

戴 姣, 刘春生, 孙景亮

(南京航空航天大学，南京 211106)

0 引言

随着科学技术的发展，控制系统的规模和复杂性不断增加，系统出现故障的机率也随之增大。任何类型故障的发生都有可能导致整个系统性能下降，甚至影响系统稳定性，造成不可预期的损失[1]。因此，提高控制系统的安全性和可靠性显得尤为重要。

根据故障处理的方式可将容错控制方法进行分类。1985年，文献[2]将容错控制分为两大类：主动容错控制(Active FTC) 和被动容错控制(Passive FTC)。被动容错控制针对的是特定的故障类型，不需要故障检测环节，其不改变控制器的参数和结构，设计方法相对简单[3]，与被动容错控制相比，主动容错控制具有更高的灵活性[4]。其在系统的故障发生之后，利用在线获得的故障信息，通过控制器的重构或者调整来保持系统的稳定性。

近年来，主动容错控制技术与鲁棒控制、最优控制、自适应控制[5]相结合，得到迅速发展。文献[6]针对执行器故障的不确定系统，利用神经网络估计系统的不确定性，并采用故障估计算法，研究了满足H-2性能要求的容错控制器；文献[7]研究了一类时变故障的不确定非线性系统的H∞容错控制问题，在线估计时变故障，利用状态信息和故障信息构成控制律以补偿故障造成的影响，使H∞性能指标最小化。

自适应动态规划(Adaptive Dynamic Programming,ADP) 是最优控制领域新兴起的一种近似最优方法，是当前研究热点。ADP方法通过函数近似结构来近似哈密顿-雅可比-贝尔曼(Hamilton-Jacobi-Bellman,HJB)方程的解，采用离线迭代[8]或者在线更新[9]的方法，来获得系统的近似最优控制策略，能够有效地解决非线性系统的优化控制问题。近年来，ADP算法用于解决连续时间和离散时间系统的时间延迟[10]、外部干扰[11]、控制受限[12]以及协同控制[13-14]、轨迹跟踪[15]等控制问题。但是有关ADP容错控制的理论研究成果很少[16]。文献[17]针对一类具有执行器故障的仿射非线性系统，提出了一种基于策略迭代算法(PI)的新型在线故障补偿方案。控制律由PI算法和故障补偿器两部分组成。文献[18]针对一类具有执行器增益故障和偏转故障的仿射非线性系统，构建积分滑模函数，利用自适应动态规划方法，得到一种滑模容错控制方案，通过构建执行网-评价网结构，得到近似最优容错控制律。

本文基于自适应动态规划方法，提出一种新的主动容错控制方案，主要创新点可概括如下：

1) 通过设计故障观测器，采用估计的执行器故障来构造性能指标函数，使其能同时反映执行器故障、状态和控制律,从而将容错控制问题转化为最优控制问题；

2) 容错控制器可以仅依赖于评价神经网络而得到，不再需要执行网络的训练；

3) 利用ADP方法来解决FTC问题，这是一种针对执行器故障的新的容错控制方法。

1 系统故障模型

考虑一类连续时间仿射非线性系统为

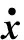
(1)

式中：x(t)∈Rn是系统的状态；u(t)=[u1…um]T∈Rm是控制输入；ua∈Rm为未知的执行器故障；f(x(t))和g(x(t))是连续可微的系统矩阵，假定f(·)和g(·)Lipchitz连续，且f(0)=0。

假设1f(·)和g(·)都是有界的。

假设2执行器故障ua未知但是满足范数有界‖ua‖≤δ1<+∞，δ1是常数，δ1>0。

针对式(1)系统，定义性能指标函数为

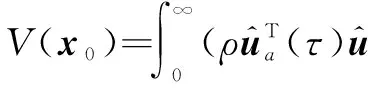
(2)

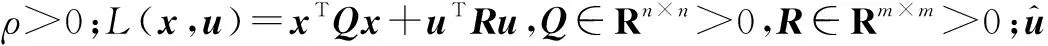
根据极小值原理，哈密顿方程可以定义为

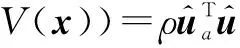
(3)

式中，▽V(x)=∂V(x)/∂x。

则最优性能指标为

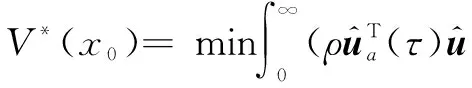
(4)

满足HJB方程

H(x，u*，▽V*(x))=0

(5)

则得最优控制律为

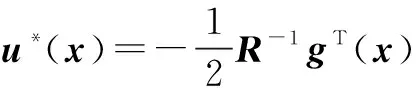
(6)

由式(6)可知，欲得最优控制策略，必须求解HJB方程。但是，直接求解式(5)的非线性HJB方程是十分困难的，几乎不可能。因此，本文利用自适应动态规划(ADP)方法求解HJB方程。

2 基于ADP的容错控制器设计

2.1 故障估计

针对式(1)的故障系统，设计故障观测器为

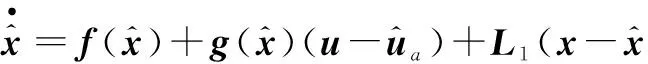
(7)

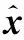
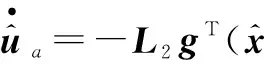
(8)

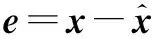
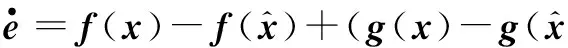
(9)

假设3e1范数有界：‖e1‖≤δ2，δ2是一个正数。

注1 因为f(x(t))和g(x(t))都是有界的，所以ef和eg均范数有界，而且，u是紧密集S上的容许控制，所以u-ua也有界，因此，假设3合理。

定理1对于式(1)的故障系统,在假设1和假设2成立的情况下，故障观测器(7)能够保证故障的观测误差最终一致有界稳定。

证明 选取Lyapunov函数

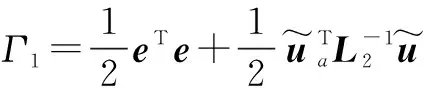
(10)

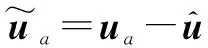
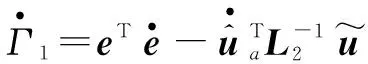
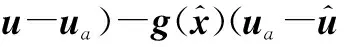
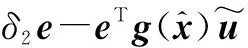
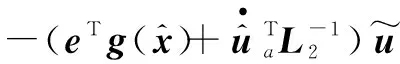
(11)

将式(8)自适应更新律代入式(11)有

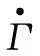
(12)

2.2 容错控制器设计

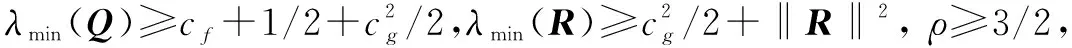
证明选取李雅普诺夫函数

(13)

然后有

(14)

基于式(5)，可得

(15)

由式(6)易得

-2Ru*(x)=gT(x)▽V*(x)

(16)

因此有

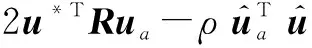
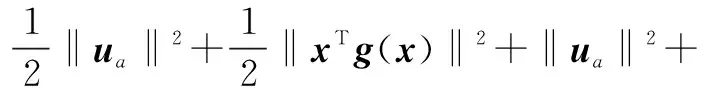
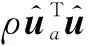
(17)

根据假设1可得

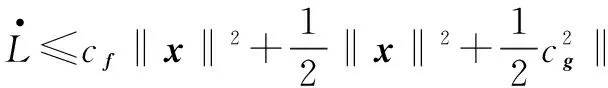
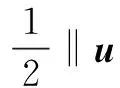
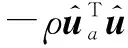
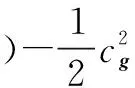
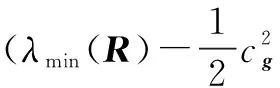
(18)

因此，当Q，R和ρ满足条件

(19)

时，系统保持渐近稳定。

3 神经网络实现

由于性能指标函数通常是高度非线性的，采用神经网络近似它[19]。 在本文中，采用单层神经网络来逼近紧密集S上的假定可微性能指标函数。

(20)

式中：wc∈Rl是理想的权值向量,l代表隐含层中的神经元个数；σ(x)∈Rl是激活函数，εc(x)表示神经网络的近似误差。式(20)中V(x)梯度为

▽V(x)=(▽σ(x))Twc+▽εc(x)

(21)

将式(8)代入式(5)中有

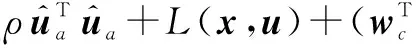
(22)

因此，哈密顿方程可以表示为

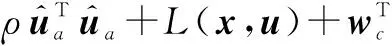
(23)

式中，eHJB表示由神经网络近似带来的残余误差。

因为理想权值向量wc是未知的，因此，评价神经网络可以近似表示为

(24)

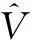
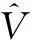
(25)

因此，近似哈密顿方程可以表示为

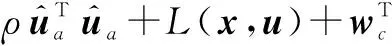
(26)

假设4评价神经网络的理想权值是有界的：‖wc‖≤w1。神经网络近似误差εc有界：‖εc‖≤ε1。激活函数σ(x)及其微分是有界的。

定义目标函数E(t)为

(27)

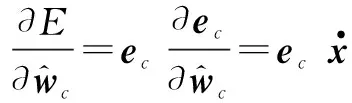
(28)

因此定义评价神经网络权值更新律为

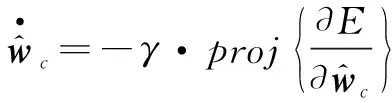
(29)

式中：γ>0是学习率；proj表示投影算子。

因此，得到近似最优控制律为

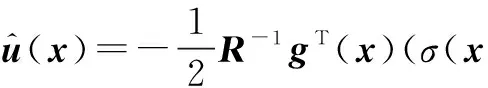
(30)

4 仿真分析

仿真结果如图1～图5所示。

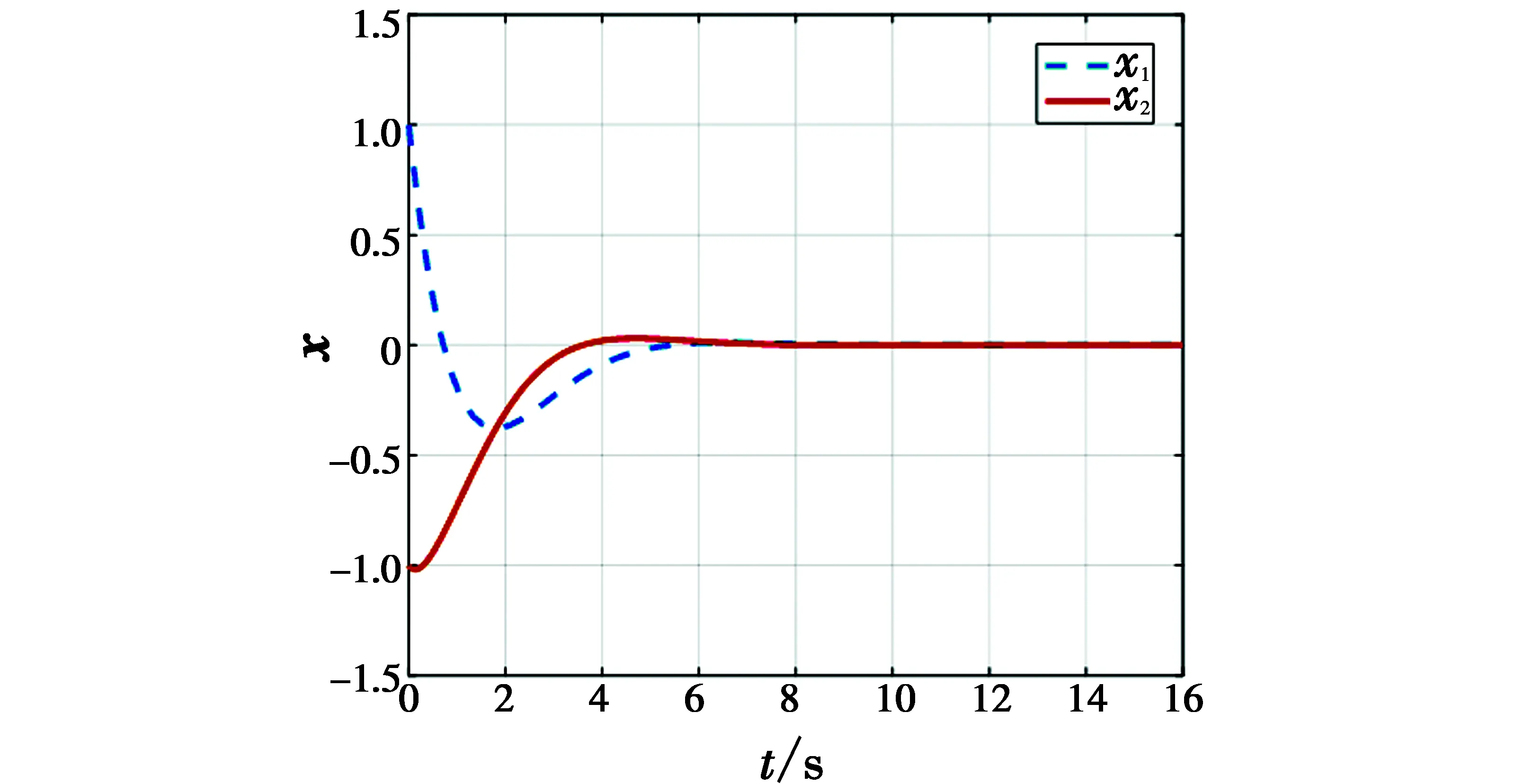
图1 无故障时系统的动态响应Fig.1 Dynamic responses with no fault

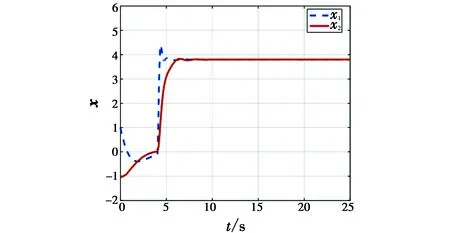
图2 未引入容错控制器的故障系统的动态响应

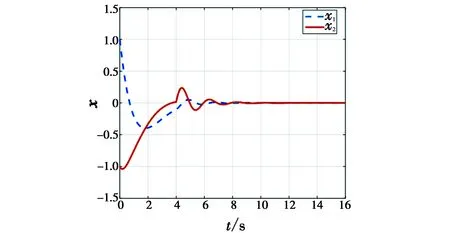
图3 容错控制器作用下的故障系统的动态响应Fig.3 Dynamic responses of the fault system under the FTC input

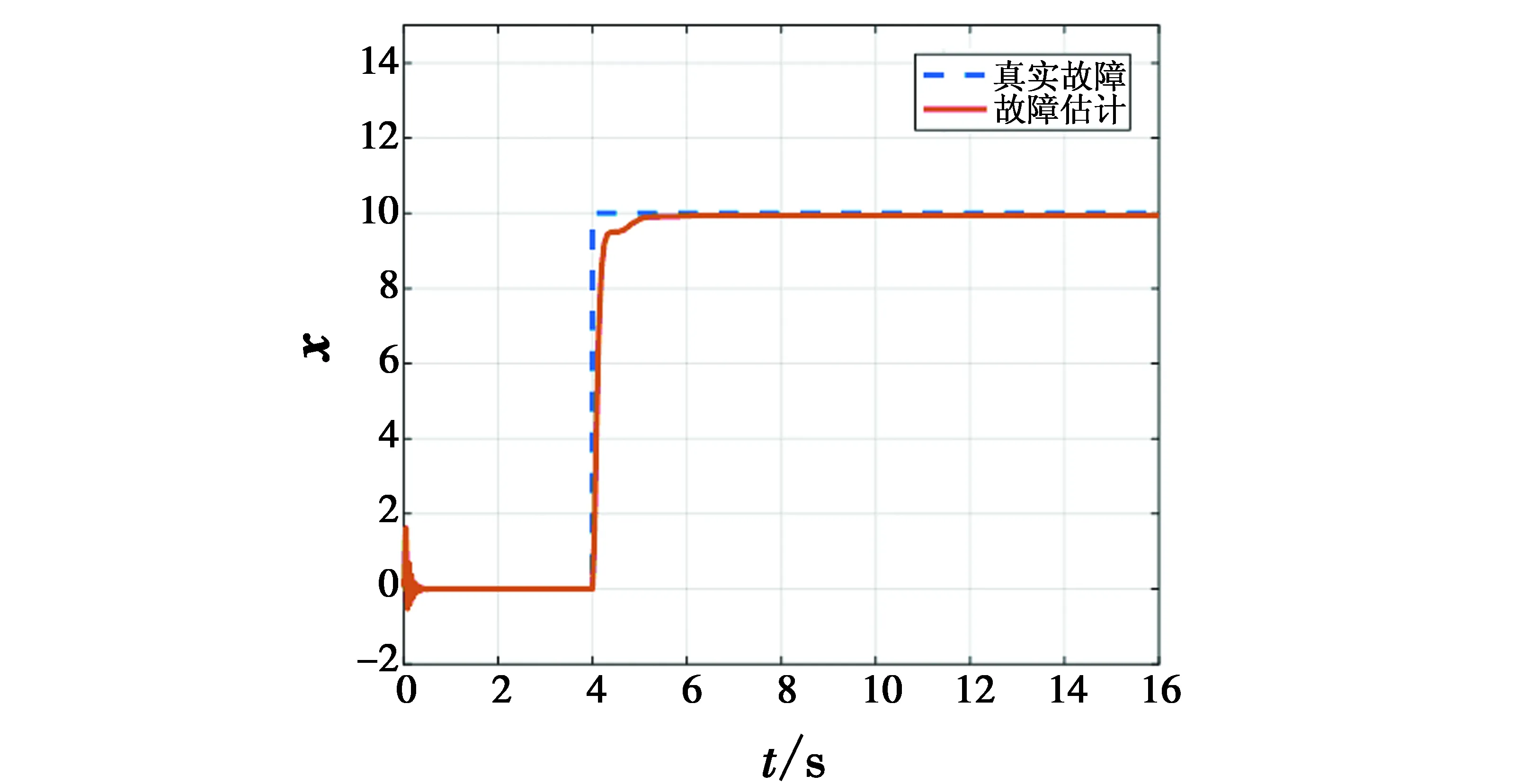
图4 基于故障观测器的故障估计Fig.4 The estimated fault based on the fault observer

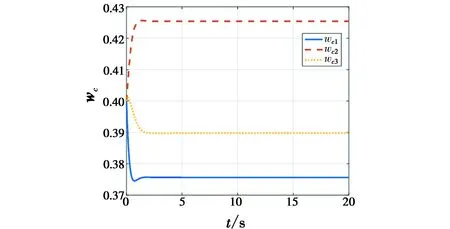
图5 评价神经网络的权值Fig.5 The weights of the critic neural network

从图5可以看出，评价神经网络的权值在设计的算法下最终收敛。执行器的故障估计是构造性能指标函数的关键，图4表明了故障观测器的故障估计值可靠有效。从图2和图1可以看出，当第4 s故障发生后，在没有引入容错控制的情况下，系统的状态受到影响并出现稳态误差，但是在图3容错控制输入的作用下，系统能很快趋于稳定，无误差。因此，仿真结果证明，本文所提出的主动容错控制方案是有效的。

5 结论

提出了一类自适应优化容错控制设计方法。为了实现主动容错控制，构造了自适应故障观测器，并将其用于容错控制律的设计，同时基于ADP算法获得近似最优容错控制律，解决了容错控制的优化问题。本文的另一特点是采用单层神经网络近似性能指标，简化了算法。仿真结果验证了本文算法的有效性，对解决一类非线性系统的执行器故障容错控制有良好的参考价值。